Division by Zero – Definition, Examples, Facts, FAQs

What Is Division by Zero in Math?

Division by zero is not defined. Division by 0 refers to a division problem having a non-zero number as a dividend (numerator) and zero as a divisor (denominator). 

Division is a process of splitting a number or a quantity into equal parts. A division problem consists of a dividend (a number to be divided), a divisor (a number by which the dividend is to be divided). The answer to the division problem is the quotient.

For instance, let us say 10 candies are to be divided between 2 people. Here, 10 is the dividend and 2 is the divisor. We write this as $10\div 2$ or $\frac{10}{2}$.

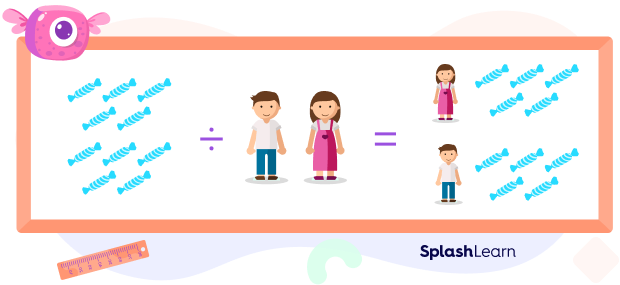
The quotient or the result will be 5, which is the number of toffees that each person will get. Remainder is 0. This is fair sharing.

Now, let’s understand what happens when you divide by zero. If 10 toffees need to be distributed between “zero” people, we can not simply divide them. 0 means nothing. The statement sounds absurd. 

Why Can’t You Divide by Zero?

Division by 0 is not defined because there is no definite answer to the problem.

Let’s try to understand using the previous example.

When we divide 10 by 2, we get

$10 \div 2 = 5 \Leftrightarrow 2 \times 5 = 10$

If we divide by 0, we can write

$10 \div 0 = ? \Leftrightarrow 0 \times ? = 10$

There is no number that you can multiply by 0 to get a non-zero result. 

How many 0s do we need to add together to get 10? 

Even if you add 0 an infinite number of times, you won’t get the answer.

Thus, the value of the quotient (?) cannot be determined. The equation can not hold true since 0 times anything is 0. Thus, division by 0 is not defined. There’s no specific answer to this problem.

Division by 0 is often represented by infinity (symbol: ). Infinity is not actually a number per se, even if it is often used like that. It represents an idea that something has no end. It goes on forever.

Consider an example.

$\frac{1}{1} = 1$ $\frac{1}{0.1} = 10$ $\frac{1}{0.001} = 1000$ $\frac{1}{0.00001} = 100000$ . . . $\text{lim}\frac{1}{x} = + \infty$ $\text{x}^{\rightarrow}0^{+}$

$\frac{1}{-1} = -1$ $\frac{1}{-0.1} = -10$ $\frac{1}{-0.001} = -1000$ $\frac{1}{-0.00001} = -100000$ . . . $\text{lim}\frac{1}{x} = \;-\; \infty$ $\text{x}^{\rightarrow}0^{-}$

As the positive number we divide by gets closer to 0, we get bigger and bigger positive numbers as a result. The answer approaches positive infinity.

In case of division by negative numbers, as the number in the denominator gets closer to 0, the answer approaches negative infinity. 

Thus, we cannot define division by 0. It is undefined.

Division Property of Zero

1. Dividing zero by any real number (except 0) will always result in 0. 

Thus, $\frac{0}{a} = 0 \div a = 0$

(Consider a real-world example here. If you divide 0 apples among 5 people, each person will get nothing. Thus, 0 divided by any non-zero real number equals 0.)

2. The answer for division by zero can be termed undefined or indeterminate. 

$\frac{a}{0} =$ Undefined …$a \neq 0$

What Is 1 Divided by 0?

For any non-zero real number, the division by 0 is not defined. Thus, one divided by zero is also not defined.

$\frac{1}{0} =$ Undefined

What Is 0 Divided by 0?

Zero divided by zero is also considered as “indeterminate form.”

$\frac{0}{0} =$ Indeterminate

Undefined vs. Indeterminate

Undefined	Indeterminate
A quantity that is not defined. There is no meaningful value. It does not exist. The operation does not make any sense.	It is defined but not known. There is a value, but it cannot be precisely determined.
There is no solution or the operation results in an invalid value. It has no meaningful interpretation.	It arises when an operation results in an infinite number of possible solutions. Value cannot be uniquely determined without additional context or information.
When a non-zero number is divided by 0, the result is undefined.	When 0 is divided by 0, it is said to be indeterminate.
$\frac{a}{0} =$ Undefined …$a \neq 0$	$\frac{0}{0} =$ Indeterminate

Facts about Division by 0

Conclusion

Division by zero is rarely encountered in real life. But the same is taught in mathematics to make children aware of possible and impossible situations. The division of any number by zero is meaningless and hence, cannot be performed. 

Solved Examples on Division by Zero

1. Simplify the expression $59 \div 0$.

Solution: 

The above statement can be written as:

$\frac{5}{9} \times \frac{1}{0} = \frac{5}{0}$

As stated, division of any number by zero is not defined. Thus, the expression is undefined. 

2. What would be the answer if we divide -4 by zero?

Solution: 

Regardless of the sign, division by zero is not possible. 

Therefore, the answer to the division of -4 by zero will be undefined. 

3. What is the value of $\frac{0}{100}$? What is the value of $\frac{100}{0}$?

Solution: 

Zero divided by any non-zero number is zero.

Thus, $\frac{0}{100} = 0$

Any non-zero number divided by 0 is not defined.

$\frac{100}{0} =$ Undefined

Practice Problems on Division by Zero

Frequently Asked Questions on Division by Zero