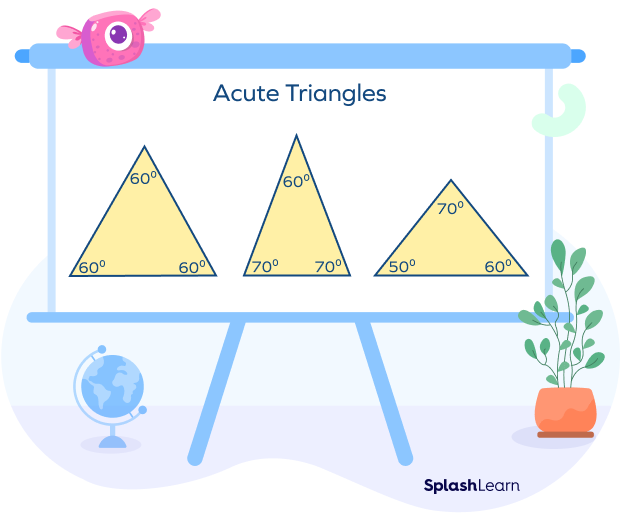
What is Acute Triangle?
A triangle is a basic polygon with three sides and three vertices. Since it has three sides, it has three interior angles. An angle that measures between 0° and 90° is called an acute angle. An acute triangle is a type of triangle in which all the three internal angles of the triangle are acute. Acute triangles are also called acute-angled triangles. Even though the length of the sides of acute triangles differs, the interior angles are never more than 90°.
Recommended Games
Types of Acute Triangles
We can categorize acute triangles into three different types based on the side length and angles of the triangles as follows.
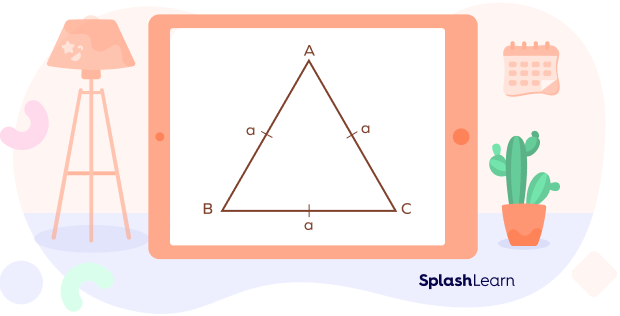
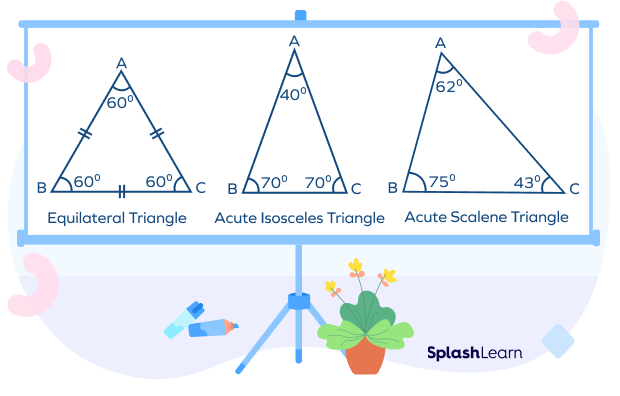
Equilateral Triangle
All the sides of an equilateral triangle are of equal lengths—each interior angle of this triangle measures 60°. So, an equilateral triangle is always an acute triangle.
In the given figure of an equilateral Triangle,
∠A = ∠B = ∠C = 60°
Side AB = Side BC = Side AC
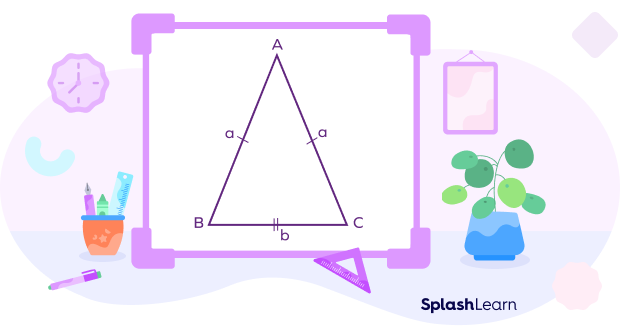
Acute Isosceles Triangle
Two sides of an acute isosceles triangle are of equal length, and angles opposite to those sides measure the same.
In the given figure of an Acute Isosceles Triangle,
∠B = ∠C ≠ ∠A
Side AB = Side AC ≠ Side BC
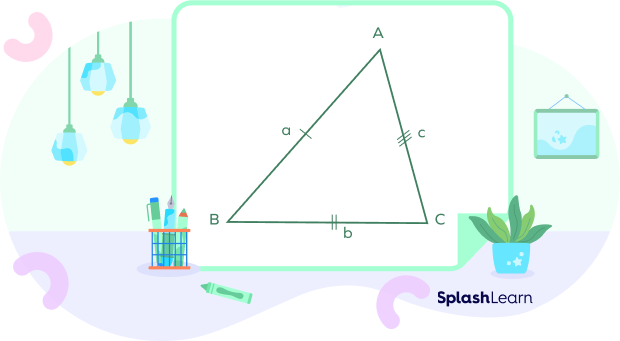
All three sides and internal angles of a scalene acute triangle are unequal. All angles measure less than 90 degrees.
In the given figure of an Acute Scalene Triangle,
∠A ≠ ∠B ≠ ∠C
Side AB ≠ Side BC ≠ Side AC
Recommended Worksheets
Acute Triangle Formulas
The basic formulas relating to an acute triangle is to calculate its perimeter and area.
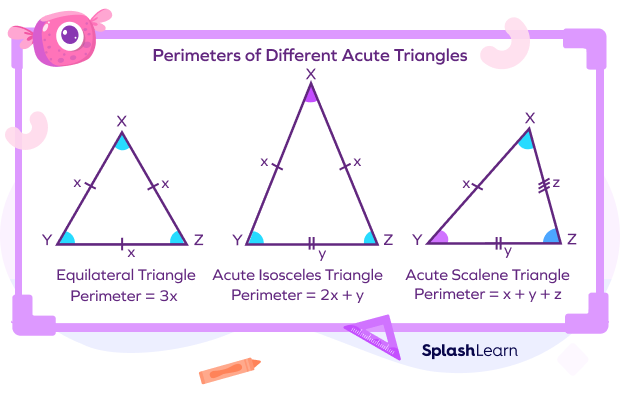
The Perimeter of An Acute Triangle
Perimeter measures the outer boundary of the given shape. The perimeter of a triangle is the sum of the length of all the sides.
Area of An Acute Triangle
The area of a triangle means the inner space covered by the three sides of the triangle.
The area of an acute triangle can be calculated using the formula of the area of a triangle.
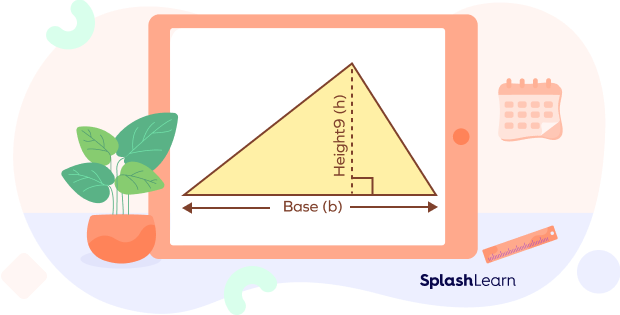
Area of triangle = (1/2) × b × h
Here, ‘b’ is the base length of an acute triangle, and ‘h’ is the height of an acute triangle.
Solved Examples on Acute Triangle
- Find the missing angle in the given figure and identify the type of triangle.
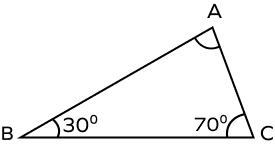
Solution:
Using the angle sum property of triangles, we get ∠A = 180° – 70° – 30° = 80°.
Since all three angles of the given triangle are different acute angles, it is an acute scalene triangle.
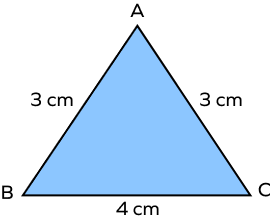
- In an acute isosceles triangle ABC, side AB = 6 cm and ∠B = ∠C. If the perimeter of this triangle is 16 cm, then find the length of the side BC.
Solution:
In the given acute isosceles triangle ABC, ∠B = ∠C. The sides opposite these angles are equal. Therefore, the lengths of the sides AB and AC must be equal.
So, AB = AC = 6 cm
The perimeter of the triangle is 16 cm. Therefore, AB + AC + BC = 16 cm.
So, the length of the side BC must be 16 – 6 – 6 or 4 cm.
- Find the area of the acute triangle whose base is 5 cm long and height is 6 cm?
Solution:
Area of an acute triangle = Area of a triangle = (1/2) × b × h.
Substituting the value of the base (b) as 5 cm long and height (h) as 6 cm, we get
Area = 1/2 × 5 × 6 = 15 cm2
Practice Problems On Acute Triangle
Acute Triangle
Which of the following angle measures can form an acute-angled triangle?
In an acute triangle, all the three angles are less than 90°. Only option a) satisfies this condition.
Identify the type of triangle.
All the three interior angles ∆ABC are acute and AB = AC. Therefore, ∆ABC is an acute isosceles triangle.
If the three interior angles of a triangle measure x, x + 20, and x + 40, then identify the type of the triangle?
Using the angle sum property of a triangle, we get $x + x + 20 + x + 40 = 180$.
So, x must be 40 and the three interior angles of the triangle are 40°, 60° and 80°.
Since all the angles of the triangle are acute but different, the triangle must be an Acute Scalene Triangle.
Frequently Asked Questions on Acute Triangle
What is an acute angle?
An angle that measures between 0° and 90° is called an acute angle. It can be measured using a protractor.
What are the properties of an acute angled triangle?
The significant properties of an acute triangle are:
- All the three interior angles of an acute triangle measures less than 90°.
- The angles of an acute triangle add up to 180°.
Is a scalene triangle always an acute triangle?
No, a scalene may not always be an acute triangle. It can be a right-angled triangle with the angles of 90°, 40°, and 50°. A scalene triangle can also be an obtuse triangle with angles as 30°, 50°, and 100°. Three interior angles of an acute triangle must be less than 90°.
Is It Possible for A Right Triangle to Be Acute?
A right triangle must have an angle that measures exactly 90°. Since the three angles of an acute triangle must be less than 90°, a right triangle cannot be acute.




























