What Is an Ordered Pair?
An ordered pair refers to two numbers written in a certain order. We generally use ordered pairs in the context of coordinates of a point in a 2D plane. It helps to locate or plot a point easily on a Cartesian plane.
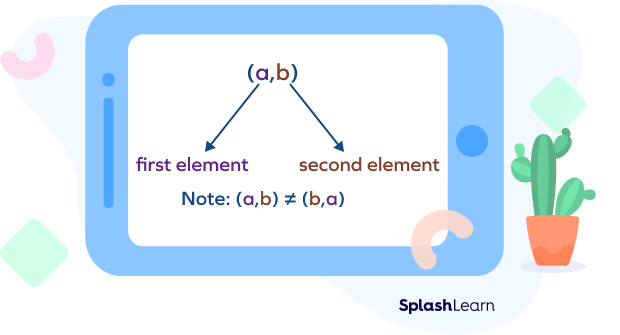
To represent an ordered pair, the two numbers are written inside the parentheses, separated by a comma, like this:
(x, y)
Here, “x” is the first element and “y” is the second element of the ordered pair.
Since the order of the elements is significant, we cannot interchange the positions of the numbers. Thus, (x, y) may not always be equal to (y, x).
Recommended Games
Ordered Pair: Definition
An ordered pair is a pair of elements or numbers written in a specific and fixed order.
On a Cartesian plane, an ordered pair (x, y) is defined as the coordinates of a point such that “x” is the x-coordinate and “y” is the y-coordinate.
Ordered pair examples: (1,2), (-4, 5), (-9, -8)
Recommended Worksheets
Ordered Pair in Cartesian Plane
The Cartesian plane is named after a French mathematician, René Descartes, who first introduced it. It is formed by the intersection of two perpendicular number lines (or axes). We call the horizontal axis the x-axis and the vertical axis the y-axis.
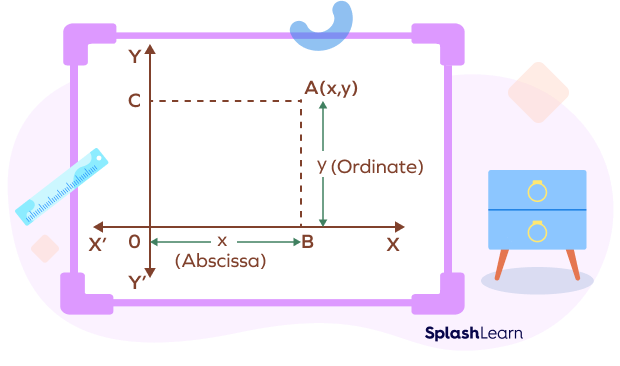
The two axes intersect at the origin. An ordered pair represents the position of a point on the coordinate plane with respect to the origin. The ordered pair (0,0) defines the position of origin. Each point on the Cartesian plane is represented by an ordered pair (x, y).
- The first element “x” is known as x-coordinate or abscissa. It defines the horizontal distance of the point from the origin
- The second element “y” is known as y-coordinate or ordinate. It defines the vertical distance of the point from the origin.
How to Graph Points Using Ordered Pairs
Step 1: Start with the first number “x” in the ordered pair or the x-coordinate.
- If x is positive, move |x| units to the right of the origin.
- If x is negative, move |x| units to the left of the origin.
Mark this point.
Step 2: Next, we will consider the second number in the ordered pair or the y-coordinate. We will move vertically up or down from the point we marked in step 2.
- If y is positive, move |y| units up from the marked point.
- If y is negative, move |y| units down from the marked point.
Step 3: The point at which we arrive in Step 2 represents the ordered pair (x, y).
(Note: |x| and |y| represent the absolute values of x and y respectively.)
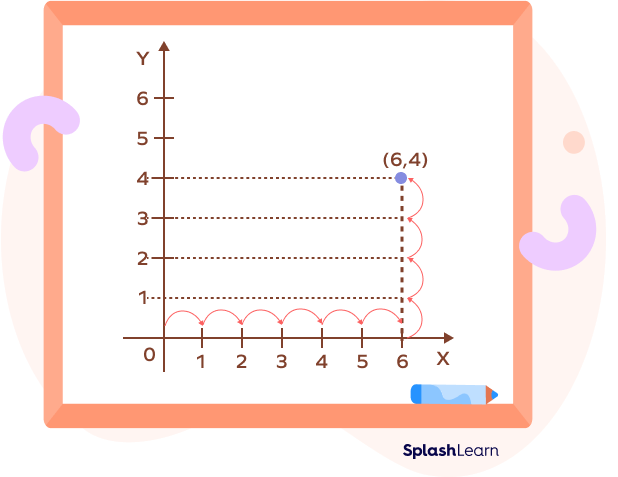
Example 1: Plot the point represented by the ordered pair (6, 4) on the Cartesian plane.
Since both x-coordinate and y-coordinate are positive, we move 6 units to the right from origin, and from there we move 4 units up.
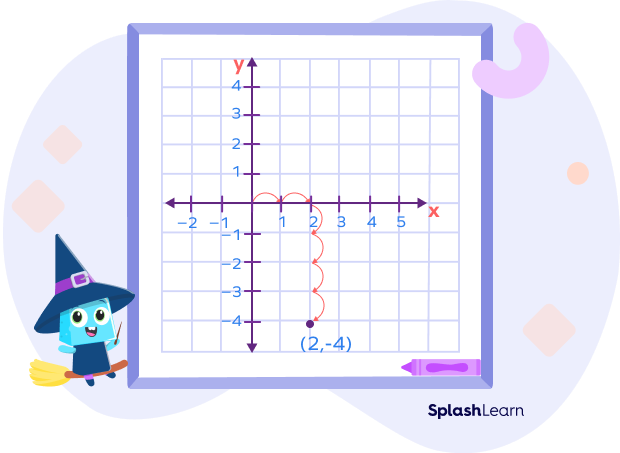
Example 2: Plot (2, –4) on a Cartesian plane.
Ordered Pairs in Different Quadrants
The x-axis (horizontal axis) and the y-axis (vertical axis) divide the Cartesian plane into 4 parts. Each of the 4 parts is known as a quadrant.
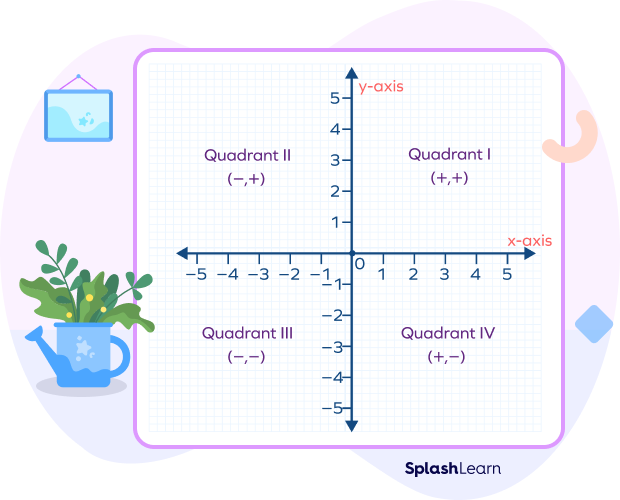
The signs of x and y in an ordered pair (x, y) in a particular quadrant can be determined on the basis of the two number lines that form axes of the given quadrant. Similarly, you can easily identify in which quadrant a given ordered pair lies.
| Quadrant | Ordered Pair Signs |
|---|---|
| I | x > 0, y > 0 |
| II | x < 0, y > 0 |
| III | x < 0, y < 0 |
| IV | x > 0, y < 0 |
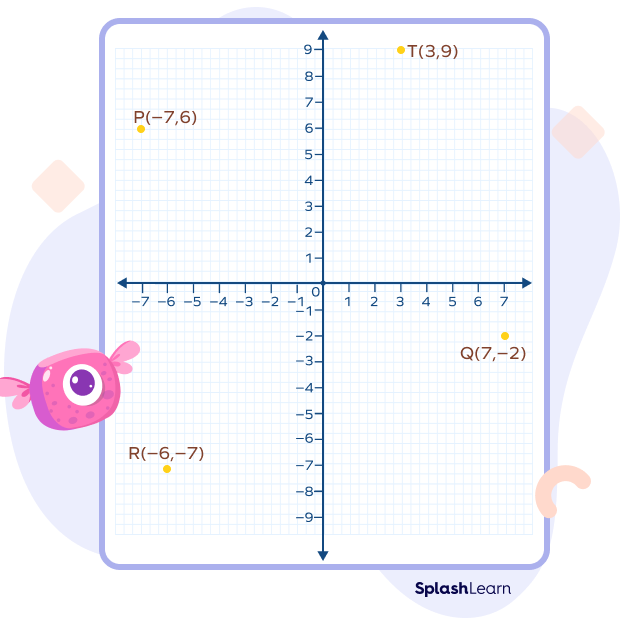
Let’s plot points using the ordered pairs (3, 9), (–7, 6), (–6, –7), and (7, –2) to observe how the signs of the numbers in the ordered pairs determine the quadrant.
| Ordered Pair (x, y) | x | y | Quadrant |
|---|---|---|---|
| (3, 9) | 3 | 9 | I |
| (–7, 6) | –7 | 6 | II |
| (–6, –7) | –6 | –7 | III |
| (7, –2) | 7 | –2 | IV |
Cartesian Product and Ordered Pairs
The cartesian product A B of two non-empty sets A and B is basically the collection of all ordered pairs (a, b) such that the first element “a” is from the set A and the second element “b” is from the set B.
$A\times B = \left\{(a,\;b) : a \in A,\; b \in B\right\}$
Example: $A = \left\{1,\; 2\right\},\; B = \left\{5,\; 6\right\}$
$A\times B = \left\{(1,\; 5), \;(1,\; 6),\; (2,\; 5),\; (2,\; 6)\right\}$
Equality Property of Ordered Pairs
If two ordered pairs are equal, then their corresponding elements are also equal. This is known as the “equality property of ordered pairs.”
If (x, y) = (a, b) then we can say that x = a and y = b.
- If (x, y) = (1, 5) then x = 1 and y = 5.
- If (a, b)= (c, d), then a = c and b = d.
- If (x + 1, y +1) = (10, 12) then x + 1 = 10 and y + 1 = 12.
Facts about Ordered Pairs
- The Cartesian plane is named after the French mathematician and philosopher René Descartes.
- If the first number of an ordered pair is 0, it means that the point lies on the y-axis. Such points have coordinates of the form (0, b).
- If the second number in an ordered pair is 0, it means that the point lies on the x-axis. Such points have coordinates of the form (a, 0).
Conclusion
In this article, we learned about ordered pairs, their representation, ordered pairs on a Cartesian plane, ordered pairs in a Cartesian product, and equality property. Let’s look at a few solved examples and practice problems.
Solved Examples on Ordered Pairs
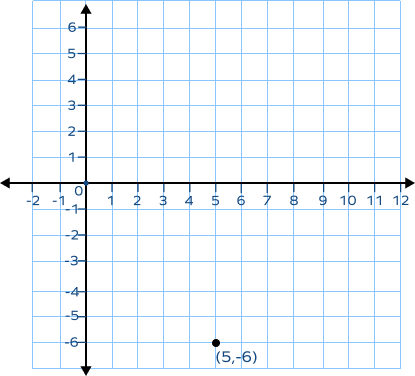
1. What does the ordered pair (5, –6) represent on the Cartesian plane?
Solution:
The first element of (5, -6) = x-coordinate = 5
It is positive.
It means that the horizontal distance of the point from origin is 5 units to the right.
The second element of (5, -6) = y-coordinate = -6
It is negative.
It means that the vertical distance from origin is 6 units down.
Based on the signs (+,–), it is clear that the point lies in the fourth quadrant.
2. In which quadrant will (–100, 150) lie?
Solution:
The x-coordinate is -100. It is negative.
The y-coordinate is 150. It’s positive.
(–, +) represents the second quadrant.
So, (-100, 150) lies in the second quadrant.
3. In which quadrants do the points (–3, –5), (8, 4), (–7, 5), (6, –3) lie on the Cartesian plane? Use the given ordered pairs to plot the points.
Solution:
(-3, -5) lies in Quadrant III .
(8, 4) lies in Quadrant I.
(–7, 5) lies in Quadrant IV.
(6, -3) lies in Quadrant II.

Practice Problems on Ordered Pairs
What Is an Ordered Pair? Definition, Facts, Examples, FAQs
Find the value of x and y if (2x + 1, 3y - 2) = (9, - 11).
By equality property, we write
2x + 1 = 9 and 3y - 2 = -11
x = 4, y = -3
Which of the following statements is false?
The order of the numbers in the ordered pair is important.
So, (x, y) $\neq$ (y, x)
We can say that (x, y) = (y, x) only if x = y.
The point (-1,-1) lies in Quadrant ____.
Ordered pairs with signs (-,-) represent points in the third quadrant.
An ordered pair of the form (x, 0) lies on the
An ordered pair of the form (x, 0) lies on the x-axis.
Frequently Asked Questions on Ordered Pairs
What is a 2-tuple?
A tuple is a finite ordered list of numbers or elements. A 2‑tuple is called an ordered pair.
Why is the order significant in an ordered pair?
An ordered pair (x, y) represents the location of a point on a Cartesian plane. Here, x is the horizontal distance of the point from the origin and y is the vertical distance of the point from the origin. If you change the order, you will get an entirely different location. The location of points (1, 2) and (2, 1) is not the same on a Cartesian plane.
How can you use ordered pairs in real life?
When you wish to analyze the relationship between two variables where one variable depends on the other, you can use ordered pairs to record data.
For example, you can record the number of people visiting a restaurant or a museum in a particular week as (5, 25), meaning 25 people visited a restaurant on the fifth day (Friday).





























