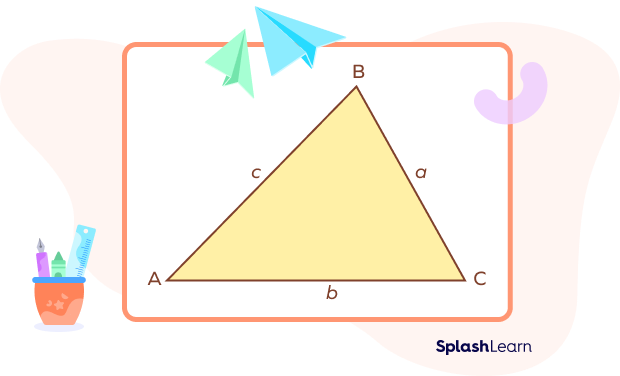
What Is the Heron’s Formula?
Heron’s formula is a mathematical formula used to find the area of a triangle when the lengths of all three sides are known.
It is named after Hero of Alexandria, an ancient Greek mathematician and engineer who first described it in his work “Metrica.” He contributed to many fields of mathematics, including geometry.
Heron’s formula is useful when you have the lengths of all three sides of a triangle and want to calculate its area without knowing the height or measurement of angles. By using this formula, you can find the area of any type of triangle, including scalene, isosceles, or equilateral triangles.
Recommended Games
Heron’s Formula Definition
Heron’s formula can be defined as a mathematical formula used to calculate the area of a triangle when the lengths of all three sides are known.
It provides a direct method to find the area without needing to know the height or angles of the triangle. It involves using the lengths of three sides and the semiperimeter of the triangle.
Area $\sqrt{= s × (s – a) × (s – b) × (s – c)}$
where:
- Area is the area of the triangle.
- s is the semiperimeter of the triangle, given by $s = \frac{a + b + c}{2}$
- a, b, and c are the lengths of the three sides of the triangle.
Proof for Heron’s Formula for Area of Triangle
We will derive Heron’s formula using the Pythagorean theorem, the area of a triangle formula, and algebraic identities.
- Consider a triangle with side lengths a, b, and c, and let the semi-perimeter be s. We aim to find the area of this triangle.
- Draw a perpendicular line from vertex B to side AC, meeting at point M. Let the length of this perpendicular be h.
- The two parts of side b, divided by the perpendicular, are p and q. Therefore, we have p + q = b.
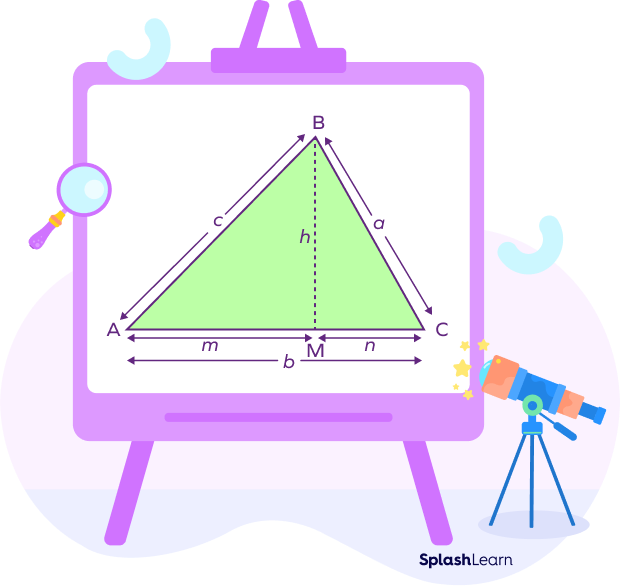
Area of a triangle $= \frac{1}{2} \times b \times h$
where,
b is the base of the triangle,
h is the height of the triangle,
From the image,
b = m + n
n = b – m ….(1)
On squaring both sides we get,
$n^{2} = b^{2} + m^{2} – 2bm$ ….(2)
Adding h2 on both sides we get,
$n^{2} + h^{2} = b^{2} + m^{2} – 2bm + h^{2}$ ….(3)
Applying Pythagoras Theorem in ▵BCM we get,
$h^{2} + n^{2} = a^{2}$ ….(4)
Applying Pythagoras Theorem in ▵MBA we get,
$m^{2} + h^{2} = c^{2}$ ….(5)
Substituting the value of (4) and (5) in (3), we get
$n^{2} + h^{2} = b^{2} + m^{2} – 2bm + h^{2}$
$a^{2} = b^{2} + c^{2} – 2bm$
$m = \frac{(b^{2} + c^{2} – a^{2})}{2b}$ ….(6)
From (5), we have $p^{2} + h^{2} = c^{2}$
$h^{2} = c^{2} – m^{2} = (c + m) (c – m)$ ….(7)
Substituting (6) in (7) we get,
$h^{2} = (c + m)(c – m)$
$h^{2} = (c + \frac{(b^{2} + c^{2} – a^{2})}{ 2b})(c – \frac{(b^{2} + c^{2} – a^{2})}{2b})$
$h^{2} = (\frac{2bc + b^{2} + c^{2} – a^{2}}{2b})(\frac{2bc – b^{2} – c^{2} + a^{2}}{2b})$
$h^{2} = (\frac{(b + c)^{2} – a^{2}}{2b})(\frac{a^{2} – (b – c)^{2}}{2b})$
$h^{2} = \frac{(b + c + a)(b + c – a)(a + b – c)(a – b + c)}{4b^{2}}$ ….(8)
As perimeter of triangle is P = a + b + c and s = semi-perimeter $= \frac{P}{2})$
∴ 2s = a + b + c ….(9)
Substituting (9) in (8), we get
$h^{2} = \frac{(b + c + a)(b + c – a)(a + b – c)(a-b+c)}{4b^{2}}$
$h^{2} = \frac{(2s \times (2s-2a) \times (2s-2b) \times (2s-2c)}{4b^{2}}$
$h^{2} = \frac{2s \times 2(s-a)\times 2(s-b) \times 2(s-c)}{4b^{2}}$
$h^{2} = 16s(s-a)(s-b)(s-c)}{4b^{2}$
$h = \frac{\sqrt{4s(s-a)(s-b)(s-c)}}{b}$ Taking square root on both sides
$h = \frac{2\sqrt{(s(s-a)(s-b)(s-c)}}{b}$ X ….(10)
Area of triangle ABC,
$A = \frac{1}{2} \times b \times h$
$A = \frac{1}{2} \times b \times \frac{2\sqrt{\left[s(s-a)(s-b)(s-c)\right]}}{b}$ (From (10))
$A = \sqrt{\left[s(s-a)(s-b)(s-c)\right]}$
∴ Area of the triangle ABC $= \sqrt{\left[s(s-a)(s-b)(s-c)\right]}$
How to Find the Area of Triangle By Heron’s Formula
The steps to find the area of a triangle using Heron’s formula are as follows:
Step 1: Find the perimeter of the given triangle.
Step 2: Calculate the semi-perimeter (s) of the triangle by adding the three side lengths and dividing by 2.
$s = \frac{a + b + c}{2}$
Step 3: Use Heron’s formula to find the area (A) of the triangle.
$A = \sqrt{s(s-a)(s-b)(s-c)}$
Step 4: Area is measured in square units. Assign the appropriate unit based on the unit of the length of sides (square inches, square meters, etc.).
Heron’s Formula for Equilateral Triangle
In an equilateral triangle, all sides have the same length. Let “a” denote the side length.
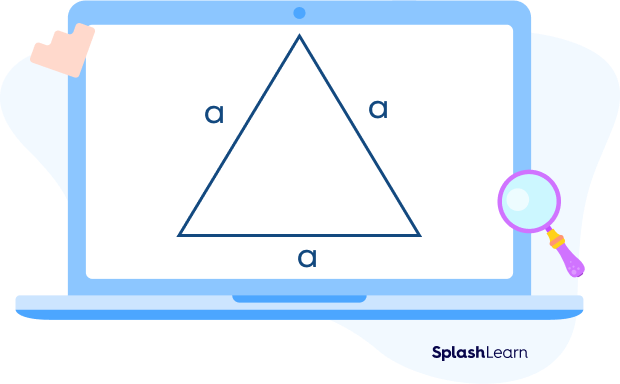
To find the area, we begin by calculating the semi-perimeter (s) of the equilateral triangle, which is half the sum of all three sides.
The semi-perimeter of the triangle is $s = \frac{a + b + c}{2} = \frac{3a}{2}$
Next, we apply Heron’s formula, which states that the area of a triangle is equal to the square root of the product of the semi-perimeter and the differences between the semi-perimeter and the lengths of its sides.
Since all sides of an equilateral triangle are equal, we have a = b = c. Therefore, the formula simplifies to:
$A = \sqrt{[s(s-a)(s-a)(s-a)}$
Simplifying further, we have:
$A = \sqrt{s(s-a)^{3}}$ where $s = \frac{3a}{2}$
This is the required formula to find the area of an equilateral triangle using Heron’s formula.
Example: Consider an equilateral triangle with all sides measuring 6 units each.
Let’s denote the length of each side as “a” = 6 units.
Area of equilateral triangle $= A = \sqrt{s(s-a)^{3}}$ where $s = \frac{3a}{2}$
Here, $s = \frac{3 \times 6}{2} = 9$ units
Area of equilateral triangle $= \sqrt{9(9 – 6)^{3}} = 15.58$ square units ((approximately)
Heron’s Formula for Scalene Triangle
For a scalene triangle, where all three sides have different lengths, we can use the original Heron’s formula to calculate its area.
The area (A) of a scalene triangle is given by:
$A = \sqrt{s(s-a)(s-b)(s-c)}$
Heron’s formula is particularly useful for scalene triangles since it allows us to calculate the area without relying on the triangle’s height or angles.
Heron’s Formula for Isosceles Triangle
An isosceles triangle has two sides that are equal in length and the angles opposite these sides are congruent. To find the area of an isosceles triangle, we can use Heron’s formula, which is modified based on the properties of the triangle.
Let’s assume “a” represents the length of the congruent sides, and “b” represents the length of the base.
The semi-perimeter (s) of the isosceles triangle is calculated by adding the lengths of the sides and dividing by 2.
$s = \frac{2a + b}{2}$
Using Heron’s formula, which calculates the area of a triangle, we substitute the side lengths of the isosceles triangle into the formula:
$Area = \sqrt{s(s-a)(s-a)(s-b)}$
This can be further simplified as:
$Area = \sqrt{s(s-a)2(s-b)}$
Alternatively, we can write it as:
$Area = (s-a)\sqrt{s(s-b)}$
This formula allows us to find the area of an isosceles triangle by substituting the known values of the congruent side length “a” and the base length “b” into the equation.
Heron’s Formula for Area of Quadrilateral
By dividing the quadrilateral into two triangles, we can use Heron’s formula to derive the formula for the area of the quadrilateral.
Consider a quadrilateral ABCD with side lengths a, b, c, and d. Let A and B be the endpoints of the diagonal, forming two triangles: ▵ADC and ▵ABC.
We can apply Heron’s formula to each of these triangles individually to find their areas.
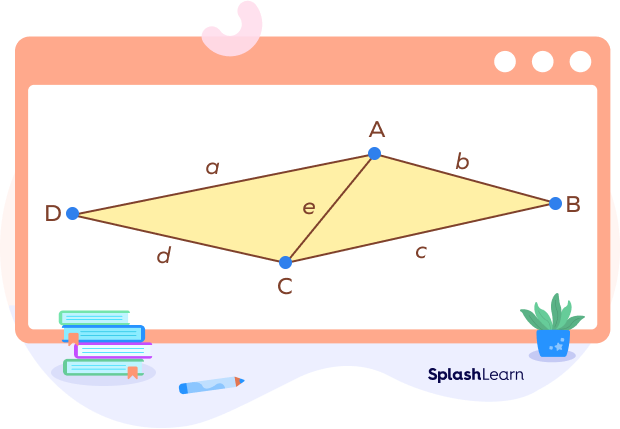
i) For ▵ADC, we can use Heron’s formula with the lengths of sides a, d, and e.
Semi-perimeter $= s = \frac{(a + d + e)}{2}$
Using Heron’s formula, the area of ▵ADC is given by:
Area of ▵ADC $= \sqrt{s(s-a)(s-d)(s-e)}$
ii) For ▵ABC, we can apply Heron’s formula with the lengths of sides b, c, and e.
Semi-perimeter $= s’ = \frac{(b + c + e)}{2}$
The area of triangle ABC is given by:
Area of ▵ABC $= \sqrt{s'(s’-b)(s’-c)(s’-e)}$
To find the area of the quadrilateral ABCD, we sum the areas of ▵ADC and ▵ABC:
Area of quadrilateral ABCD = Area of ▵ADC + Area of ▵ABC
Therefore, the area of the quadrilateral ABCD can be calculated as:
Area of quadrilateral ABCD $= \sqrt{s(s-a)(s-d)(s-e)} + \sqrt{s'(s’-b)(s’-c)(s’-e)}$
By substituting the appropriate side lengths into the formula, we can determine the area of the quadrilateral using Heron’s formula.
History of Heron’s Formula
- Heron’s formula is attributed to Heron of Alexandria, a mathematician from ancient times.
- Heron developed the formula around 60 CE and documented it in his work called “Metrica.”
- This formula enabled the calculation of a triangle’s area without needing its height or angles.
- Heron’s formula was groundbreaking as it expanded to compute quadrilateral areas, highlighting his mathematical prowess.
- Beyond area calculations, Heron harnessed his formula to delve into trigonometric concepts like the Laws of Cosines and Cotangents.
- These trigonometric principles are fundamental in geometry and find application in diverse fields such as physics, engineering, and navigation.
Facts on Heron’s Formula
- Heron’s formula is used to find the area of a triangle when the lengths of all three sides are known. It is applicable to all types of triangles, including scalene, isosceles, and equilateral triangles.
- The formula involves calculating the semi-perimeter (s) of the triangle, which is half the sum of the three side lengths: $s = \frac{a + b + c}{2}$.
- Heron’s formula allows calculating triangle area without needing height or angles information.
- In some cases, Heron’s formula can be used to find the area of certain quadrilaterals by dividing them into two triangles and applying Heron’s formula to each triangle.
- Heron’s formula can be extended to find the area of cyclic quadrilaterals, where all four vertices lie on a common circle. This extended formula, known as Brahmagupta’s formula, calculates the area of such quadrilaterals based on their side lengths.
Conclusion
In this article, we explored Heron’s Formula and its historical significance, dating back to ancient times. Heron of Alexandria’s contributions to geometry and trigonometry through this formula have left a lasting impact on various fields. We also discussed the formula for different types of triangles and quadrilaterals. To reinforce our understanding, let’s delve into practical examples and engage with MCQs for enhanced comprehension.
Solved Examples on Heron’s Formula
Example 1: A scalene triangle has side lengths of 8 inches, 15 inches, and 17 inches. Calculate its area.
Solution:
Lengths of the sides: a = 8, b = 15, c = 17
Now let’s calculate the semi-perimeter (s):
$s = \frac{(a + b + c)}{2}$
$s = \frac{(8 + 15 + 17)}{2}$
$s = \frac{40}{2}$
s = 20 inches
According to Heron’s formula:
$Area (A)= \sqrt{s(s-a)(s-b)(s-c)}$
$Area (A)= \sqrt{20(20-8)(20-15)(20-17)}$
$Area (A)= \sqrt{20(12)(5)(3)}$
$Area (A)= \sqrt{20(12)(5)(3)}$
$Area (A)= \sqrt{3600}$
Area (A)= 60 square inches
So, the area of the scalene triangle is 60 square inches.
2. Find the area of an isosceles triangle with equal sides of length 10 inches each and a base of length 12 inches.
Solution:
a = 10, b = 12
Now let’s calculate the semi-perimeter (s):
$s = \frac{a + a + b}{2}$
$s = \frac{10 + 10 + 12}{2}$
$s = \frac{32}{2}$
s = 16 inches
According to Heron’s Formula for area of isosceles triangle:
$Area (A)= (s-a)\sqrt{s(s-b)}$
$Area (A)= (16-10)\sqrt{16(16-12)}$
$Area (A)= (6)\sqrt{16(4)}$
$Area (A)= 6\sqrt{64}$
$Area (A)= 6\times8$
Area (A)= 48 square inches
So, the area of the isosceles triangle is 48 square inches.
Example 3: Find the area of the quadrilateral PQRS shown in the figure below using Heron’s formula.
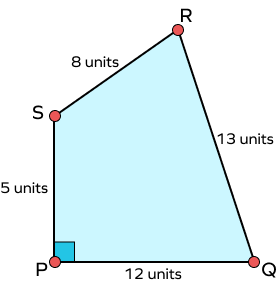
Solution:
Here, PQ and PS are perpendiculars. So, triangle PQS is a right angled triangle. Thus, the Pythagoras theorem can be used to calculate the length of diagonal QS of quadrilateral PQRS:
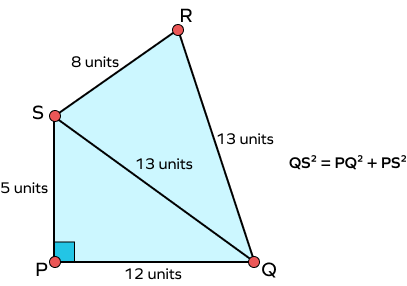
In PQS, PQ = 12 units, PS = 5 units
According to Pythagoras theorem,
$PQ^{2} + PS^{2} = QS^{2}$
$12^{2} + 5^{2} = QS^{2}$
$144 + 25 = QS^{2}$
$169 = QS^{2}$
$QS = \sqrt{169} =13$ units
Now, let’s find the area of PQS:
a = 12 units, b = 13 units and c = 5 units
$s = \frac{(a+b+c)}{2} = \frac{(12+13+5)}{2} = \frac{30}{2} = 15$ units
$A = \sqrt{s(s-a)(s-b)(s-c)}$
$A = \sqrt{15(15-12)(15-13)(15-5)}$
$A= \sqrt{15(3)(2)(10)}$
$A= \sqrt{15(3)(2)(10)}$
$A = \sqrt{900}$
$A = 30\; unit^{2}$
Area of ΔPQS $= 30\; unit^{2}$
Now QRS is an isosceles triangle as the two adjacent sides are equal.
Here, a = 13 and b = 8
$s = \frac{(2a+b)}{2} = \frac{26 + 8}{2} = \frac{34}{2} = 17$
$Area= (s-a)\sqrt{\left[s(s-b)\right]}$
$Area= (17-13)\sqrt{\left[17(17-8)\right]}$
$Area= (4)\sqrt{\left[17(9)\right]}$
$Area= (4)\sqrt{153}$
$Area= 4 \times 12.369$
$Area= 49.476$
Area of Δ QRS $= 49.476\; unit^{2}$
Area of PQRS = Area of triangle PQS + Area of triangle QRS
Area of PQRS $= (30 + 49.476)\; unit^{2} = 79.476 unit^{2}$.
Therefore, the area of the quadrilateral is $79.476 \;unit^{2}$.
Practice Problems on Heron’s Formula
Heron’s Formula - Definition, Formula, Proof, Facts, Examples
What does Heron's formula calculate?
Heron's formula calculates the area of a triangle based on the lengths of its sides.
Which type of triangles can Heron's formula be used for?
Heron's formula can be used for all types of triangles, including right-angled, scalene, isosceles, and equilateral triangles.
What is the semi-perimeter of a triangle?
The semi-perimeter of a triangle is half of the perimeter, calculated as (a + b + c) / 2, where a, b, and c are the side lengths.
How many side lengths of a triangle are required to use Heron's formula?
Heron's formula requires all three side lengths of the triangle to calculate its area.
Which theorem does Heron's formula indirectly relate to in the case of a right-angled triangle?
Heron's formula indirectly relates to the Pythagorean theorem in the case of a right-angled triangle.
Frequently Asked Questions about Heron’s Formula
Can Heron’s formula be used to find the area of a quadrilateral?
It is not directly applicable to find the area of quadrilaterals. However, in certain cases, by dividing the quadrilateral into two triangles, we can apply Heron’s formula to each triangle, and calculate the total area of the quadrilateral.
Can I use Heron’s formula if I only know the angles of the triangle?
No, Heron’s formula requires the lengths of the triangle’s sides, not just the angles. It is specifically designed to calculate the area based on side lengths.
Is Heron’s formula the only method to calculate the area of a triangle?
No, there are other methods to find the area of a triangle, such as using the base and height, using trigonometric functions, or using unit squares depending on the information available.

















