Solving Multi Step Equations – Definition, Facts, Examples, FAQs

What Are Multi-step Equations?

The multi-step equations are algebraic equations that require multiple steps (more than two steps) to solve. 

Solving multi-step equations in algebra is similar to solving one-step and two-step equations, but the process is a little lengthy as there are multiple steps involved.

Examples of Multi-step Equations:

• $3 (4x \;-\; 5) = 4x \;-\; 7$
• $-\;1\left[(\frac{1}{7})m + \frac{1}{6}\right] = 4$
• $10 \;-\; (2t + 3) = (3t \;-\; 5) + 20$

We are familiar with solving one-step and two-step equations. 

• One-step equations are equations that can be solved in a single step. 
• Two-step equations require only two steps to solve.

Multi-step equations involve more complex operations. For solving the multi-step equations, we just extend the same process. 

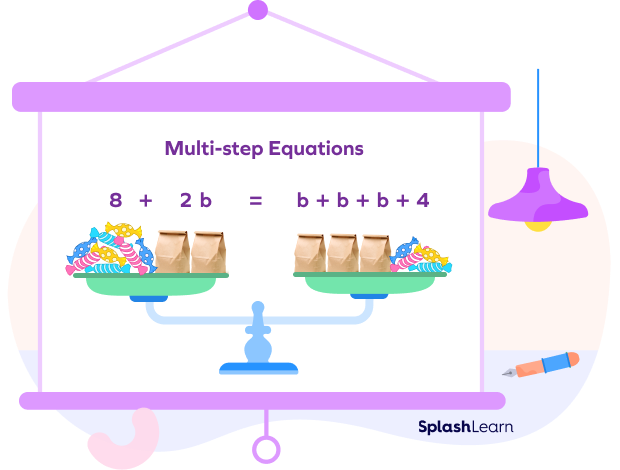
Multi-step Equations: Definition

Multi-step equations are the equations in which we have to use multiple steps (to undo more than two operations) to isolate the variable and solve. 

Inverse Operations Used for Solving Multi-step Equations

To solve the multi-step equations, we need to isolate the variable. We can do that by applying the inverse operation on both sides. To balance the equation, we apply the same operation on both sides. 

Operation	Inverse Operation
Addition (+)	Subtraction (-)
Subtraction  (-)	Addition (+)
Multiplication $(\times)$	Division $(\div)$
Division $(\div)$	Multiplication $(\times)$

Also, powers and roots are the opposite operations which undo each other.

How to Solve Multi-step Equations

Step 1: Simplify both sides of the equation by expanding the brackets, combining like terms, and using the distributive property if necessary.

Step 2: Isolate the variable term by performing inverse operations on both sides of the equation.

Step 3: Continue simplifying until the variable term is isolated on one side and all other terms are shifted to the other side.

Step 4: Solve for the variable by performing the necessary operations to isolate the variable.

Step 5: Verify your solution by substituting the value back into the original equation.

Example 1: $2x + 5 \;-\; 3(2 \;-\; x) = 4x \;-\; 7$

$2x + 5 \;-\; 3(2 \;-\; x) = 4x \;-\; 7$

$2x + 5 \;-\; 6 + 3x = 4x \;-\; 7$ …expanding the bracket

$2x + 3x \;-\;4x + 5 \;-\; 6 = \;-\; 7$ …combining like terms

$x + 5 \;-\; 6 = \;-\; 7$

$x = 6 \;-\; 5 \;-\; 7$ …isolating the variable

$x = \;-\; 6$

Example 2: $–\; 2(y + 3) = 3(y \;–\; 7) + 5$

$–\; 2(y + 3) = 3(y \;–\; 7) + 5$

$\;–\; 2y \;–\; 6 = 3y \;–\; 21 + 5$ …applying the distributive property 

$–\; 2y \;–\; 6 = 3y \;–\; 21 + 5$

$–\; 2y \;–\; 6 = 3y \;–\; 16$

$–\; 2y \;–\; 3y \;–\; 6 = 3y \;–\; 3y \;–\; 16$ …combining like terms

$–\; 5y \;–\; 6 = \;–\; 16$

$–\; 5y = \;– \;10$ …adding 6 on both sides

$y = \frac{-\;10}{-\; 5}$ …dividing both sides by -5

$y = 2$

Solving Multi-step Equations Involving Fractions

If a multi-step equation involves one or more fractions in them, we need to apply the rules for adding or subtracting fractions with same or different denominators when solving the equation. 

To get rid of fractions, use the following steps:

Step 1: Find the Least Common Denominator (LCD) of all the denominators to make the denominators same.

Step 2: Multiply each and every term on both sides of the equation by LCD.

Step 3: Apply inverse operations and isolate the variable.

Example:

$\frac{m}{5} + \frac{1}{6} = \frac{1}{3} + \frac{1}{2}m$

Step 1: The denominators are 2, 3, 5, and 6.

LCM of 2, 3, 5, and 6 is 30.

LCD of $\frac{1}{5},\;\frac{1}{6},\;\frac{1}{3}$, and $\frac{1}{2}$ is 30.

Step 2: Multiply each term on both sides by 30.

$30(\frac{m}{5} + \frac{1}{6}) = 30(\frac{1}{3} + \frac{1}{2}m)$

$6m + 5 = 10 + 15m$

Now, the above equation is simplified and free from fractions. 

Subtracting 6m and 10 from both the sides, we get

$6m + 5\;-\;6m\;-\;10 = 10\;-\;10 + 15m\;-\;6m$

$-\;5 = 9m$

Dividing both the sides by 9, we get

$m = \frac{-\;5}{9}$

Multi-step Equations: Word Problems

Sometimes we have to form the equation using the information provided in the word problem.

Example: Find the angle measures of a triangle if the first angle is thirty degrees more than

the second, and the third is ten degrees less than twice the first.

Let the three vertices of a triangle be A, B, and C. We know that the sum of three angles of a triangle is 180^o.

Thus, m∠A + m∠B + m∠C = 180^o …(1)

Suppose that the first angle be ∠A. The first angle is thirty degrees more than the second.

m∠A = m∠B + 30^o

Let m∠B = x

Thus, m∠A = x + 30^o …(2)

The third angle is ten degrees less than twice the first.

m∠C = 2 m∠A – 10^o

But m∠A = x + 30^o

Thus, m∠C = 2 (x + 30^o) – 10^o

m∠C = 2x + 50^o …(3)

Substitute the values from (2) and (3) in (1).

m∠A + m∠B + m∠C = 180^o

x + 30 + x + 2x + 50 = 180^o

x + x + 2x + 80= 180^o

4x = 100^o

x= 25^o

Thus, m∠B = x = 25^o

 m∠A = x + 30^o = 55^o

 m∠C = 2x + 50^o = 100^o

Facts about Multi-step Equations

Conclusion

In this article, we learned about multi-step equations, how to solve them, and a few examples to understand the steps involved. Let’s solve a few multi-step equations and practice problems based on multi-step equations for better understanding.

Solved Examples on Multi-step Equations

1. Find the solution of $\frac{1}{2}(2x \;-\; 4) = 11$

Solution:

$\frac{1}{2}(2x\;-\;4) = 11$

Multiply both sides by 2, we get

$(2x\;-\;4) = 11 \times 2$

$2x\;-\;4 = 22$

Adding 4 on both sides, we get

$2x\;-\;4 + 4 = 22 + 4$

$2x = 26$

Dividing both the sides by 2, we get

$x = \frac{26}{2}$

$x = 13$

2. Solve: $\frac{1}{4}x\;-\;\frac{3}{4} = 2x + 3$

Solution:

$\frac{1}{4}x\;-\;\frac{3}{4} = 2x + 3$

Multiplying both the sides by 4, we get

$x\;-\;3 = 8x + 12$

Subtracting 8x and adding 3 from both the sides, we get

$x\;-\;3\;-\;8x + 3 = 8x + 12\;-\;8x + 3$

$-\;7x = 15$

$x =\frac{-\;15}{7}$

3. Solve the equation for “m”: $4(5s + 3) = 12$

Solution:

$4(5s + 3) = 12$

Distributing 4 on LHS, we get

$20s + 12 = 12$

Subtracting 12 from both sides, we get

$20s + 12 \;-\; 12 = 12 \;-\; 12$

$20s = 0$

Dividing both sides by 20, we get

$s = 0$

4. Solve $\frac{x}{4} \;-\; 5 = 3x$ for x.

Solution: 

The given equation is:

$\frac{x}{4}\;-\;5 = 3x$

Multiply each term on both sides by 4.

$x\;-\;20 = 12x$

Subtracting x from both sides, we get

$x\;-\;20\;-\;x = 12x\;-\;x$

$-\;20 = 11x$

Dividing both sides by 11, we get

$x = \frac{-\;20}{11}$

5. Mia is 5 years older than Molly. After 5 years, the sum of their ages is 25. Then how old is Mia now?

Solution: 

Suppose that Molly’s current age is x years. 

Mia’s age = x + 5.

Molly’s age after 5 years = x + 5

Mia’s age after 5 years = x + 10

Sum of their ages after 5 years = 25

(x + 5) + (x + 10) = 25

2x + 15 = 25 Combining like terms

2x = 10 Subtracting 25 from both sides

x = 5 Dividing both sides by 2

Molly’s age = 5 years

Mia’s age = 5 + 5 = 10 years

Practice Problems on Multi-step Equations

Frequently Asked Questions about Multi-step Equations