What Are Compatible Numbers?
Compatible numbers in math are the numbers that are easy to add, subtract, multiply, or divide mentally. They are close in value to the actual numbers, which makes estimating the answer and computing problems easier. Let us see how they make calculations easier using an example.
Kate wants to buy a hoverboard and a safety helmet. The price of the hoverboard is $\$244$ and the price of the safety helmet is $\$38$. Kate has only $\$275$ in hand. She wants to know if she has enough money to buy both items. Using compatible numbers, Kate can estimate the total cost mentally without actually adding 244 and 38.
$244 + 38 =$ ?
$240 + 40 = 280$
Now she knows that she needs more money to buy the hoverboard and the helmet.
Recommended Games
Where Do We Use Compatible Numbers in Math?
If we want to find an estimate or to approximate a calculation, we can replace the actual numbers with compatible numbers. They are commonly used to solve problems where some inaccuracy is acceptable or approximation is allowed. The answer won’t be exact but a reasonable estimate.
Let us see how we can perform addition, subtraction, multiplication, and division easily using compatible numbers.
Recommended Worksheets
Compatible Numbers in Addition
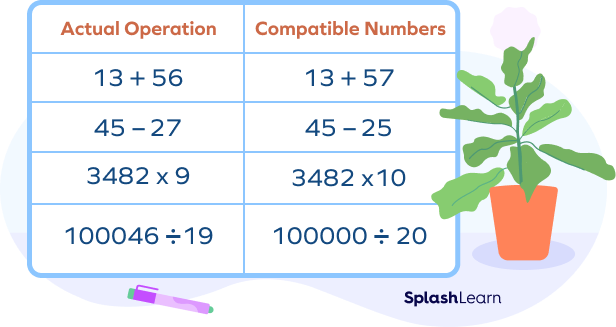
When calculating the sum of two or more numbers, the numbers ending with 5 or 0 are always easy to work with. Examples: $65 + 15 = 80$
Also, the number pairs that add up to a multiple of 10 (or a number ending with 0) also make the addition easier. A pair of numbers ending with 1 and 9, 2 and 8, 3 and 7, 4 and 6, 5 and 5 are compatible.
Examples: $18 + 22 = 40, 13 + 7 = 20, 11 + 19 = 30$
We can round the numbers to the nearest ten, hundred, thousand or ten thousand. Let’s see an example.
Example 1: Numbers rounded to the nearest ten, hundred, or thousand.
For instance, if we have to add 493 and 549, we can make the numbers compatible by rounding them up to the nearest tens or hundreds.
493 and 549 rounded to the nearest tens become 490 and 550 respectively.
493 and 549 rounded to the nearest hundreds become 500 and 500 respectively.
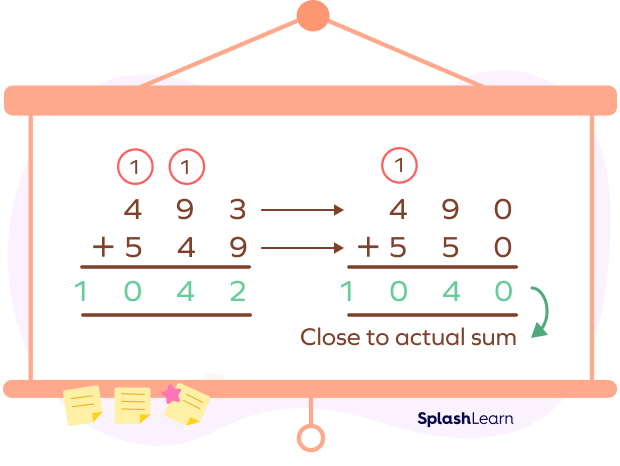
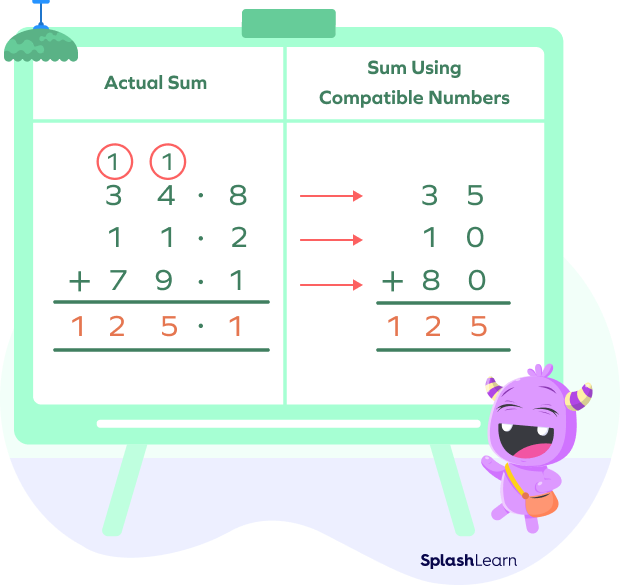
Example 2: Estimating the addition of decimal numbers.
Example 3: Add 58 and 13.

Compatible Numbers in Subtraction
Like addition, the numbers ending with zeroes are compatible in subtraction as well. Also, the numbers having the same last digit help in finding the difference.
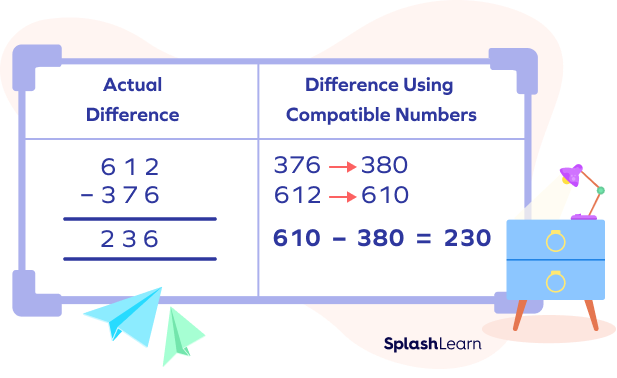
Example 1: Subtract 376 from 612.
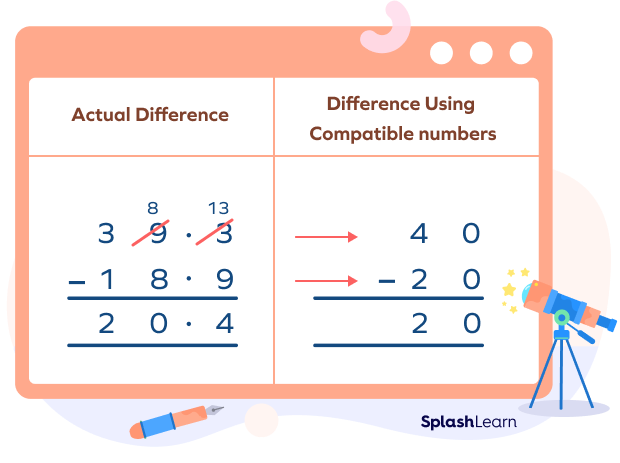
Example 2: Subtracting decimals.
Example 3: Numbers ending with the same digit.

Compatible Numbers in Multiplication
It is always easy to multiply numbers ending with one or more zeros. We can ignore them in the beginning and multiply the non-zero numbers first. Once the multiplication is complete, the appropriate number of zeros can be added.
Example 1: Multiply 62 with 13.
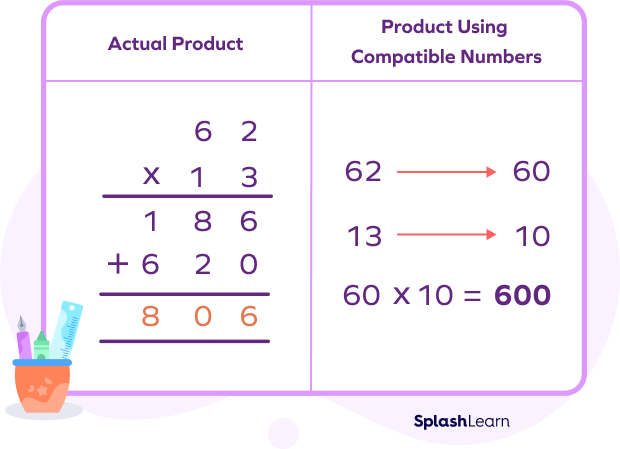
Example 2: Multiplying decimals

Example 3: Numbers whose multiplication tables we know so that we can multiply easily.
Actual product of $34$ and $9 = 34 \times 9 = 306$
Using compatible numbers, we get: $34 \rightarrow 34$ and $9 \rightarrow 10$
Product using compatible numbers: $34 \times 10 = 340$
Compatible Numbers in Division
Numbers that end with 1 or more zeros are compatible in division as well.
Example 1: Numbers rounded to the nearest ten, hundred, or thousand.

Example 2: Dividing decimals using compatible numbers.
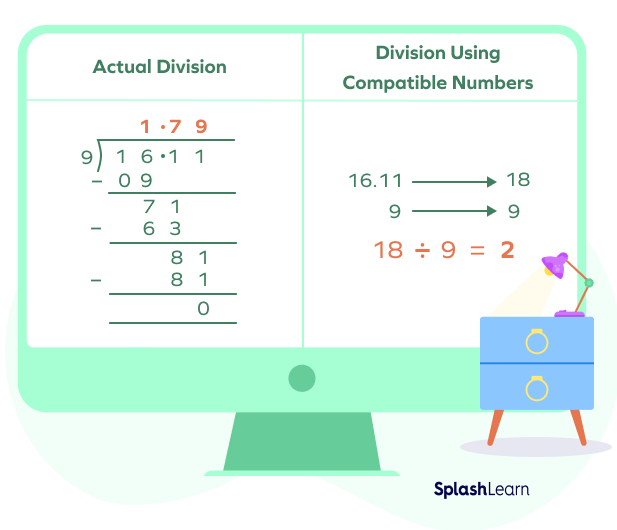
Example 3: Numbers whose multiplication tables we know so that we can divide easily.
Actual quotient by dividing $70$ and $4: 70 \div 4 = 17.5$
Using compatible numbers, we get: $70 \rightarrow 68$ and $68 \div 4 = 17$
Important Note: When estimating with division, if you decrease the value of one number, you should also decrease the value of the other. If you increase the value of one number, you should increase the value of the other. This helps to keep the estimate as close as possible to the exact answer.
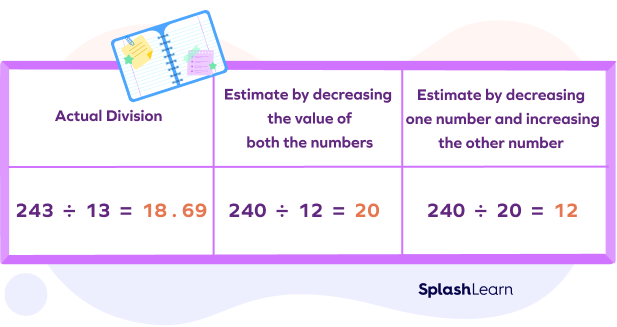
We can see that we get a closer estimate when we decrease the value of both the numbers than when we decrease the value of one and increase the value of the other.
Compatible Numbers and Estimation
Compatible numbers are often used to estimate values by converting actual values to numbers that are easy to calculate mentally.
Example: Dean saved $\$37$ and Tom saved $\$52$. Estimate the total amount saved by the brothers.
First, replace the numbers with compatible numbers:
$\$37$ is replaced by $\$40$
$\$52$ is replaced by $\$50$
$\$40 + \$50 = \$90$
Dean and Tom saved around $\$90$ altogether.
If there are more complicated values, we try to balance how we estimate the values.
For example, if in one case we estimate $\$37$ as $\$40$, we should try to round off the other number down by a similar amount if possible. This way our estimate will be more accurate.
Compatible Numbers v. Rounding
Compatible numbers and rounding are rather similar, but there is a slight difference between them. We pick closer numbers to make it easier to solve a problem in compatible numbers.
Example: Raj wants to divide his study time of 166 minutes equally among 4 subjects.
Actual division: 166 divided by 4 is 41.5 minutes per subject.
Using compatible numbers, we can solve this as: $166$ -\gt 160$
160 divided by 4 gives 40 minutes per subject.
Rounding 166 to the nearest tens gives 170. Dividing 170 by 4 gives 42.5 minutes per subject.
Conclusion
We learned about compatible numbers, which make complex calculations involving addition, subtraction, multiplication or division pretty easy. Next time you are standing in the queue to get your groceries billed, use the compatible numbers to find the total quickly before the person at the billing counter does.
Solved Examples on Compatible Numbers
Estimate the following using compatible numbers.
- $83 + 18$
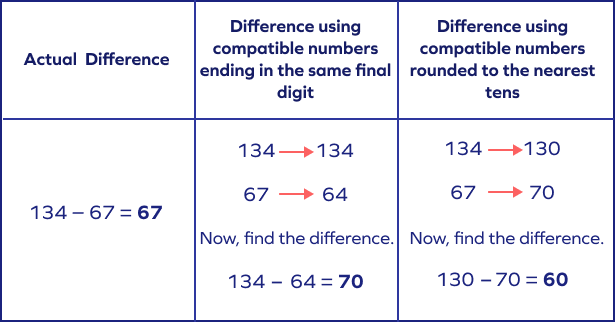
- $134 − 67$
- $319 \times 89$
- $7810 \div 37$
Solution: Compatible numbers are the numbers that are easy to add, subtract, multiply, or divide mentally.
- $83 + 18$
Replace the numbers with compatible numbers of addition.
$83 \rightarrow 80$
$18 \rightarrow 20$
Now, find the sum.
$80 + 20 = 100$
- $134 − 67$
Here, we can use compatible numbers in two different ways.
(c) $319 \times 89$
Replace the numbers with compatible numbers of multiplication.
$319 \rightarrow 300$
$89 \rightarrow 90$
Now find the product.
$300 \times 90 = 27,000$
(d) $7810 \div 37$
Replace the numbers with compatible numbers of division.
$7810 \rightarrow 8000$
$37 \rightarrow 40$
Now, find the quotient.
$8000 \div 40 = 200$
2. Lisa went shopping and swiped her card for $\$487$ in the first shop and $\$192$ in the second shop. Estimate how much she spent in both the shops together?
Solution:
Amount Lisa swiped in the first shop $= \$487$
Amount Lisa swiped in the second shop $= \$192$
Amount spent by Lisa in both the shops $= \$487 + \$192$.
To find the estimate we replace the numbers with compatible numbers.
$\$487 \rightarrow \$500$
$\$192 \rightarrow \$200$
$\$500 + \$200 = \$700$
Lisa spent around $\$700$ in both the shops together.
3. A pastry shop got an order of 3897 donuts. If each box can hold 4 donuts, approximately how many boxes will the shop need?
Solution:
Number of donuts to be packed $= 3897$
Number of donuts per box $= 4$
Number of boxes needed to pack all the donuts $= 3897 \div 4$
To find the estimate we replace the numbers with compatible numbers.
$3897 \rightarrow 4000$ and $4\rightarrow4$
$4000 \div 4 = 1000$
The shop needs around 1000 boxes to pack 4132 donuts.
4. John’s bank account had a balance of $\$693$. If he withdrew $\$129$, what is his approximate new balance?
Solution:
John’s account balance $= \$693$
Amount John withdrew $= \$129$
John’s new account balance $= \$693 − \$129$
To find the estimate we replace the numbers with compatible numbers.
$693\rightarrow693$
$129\rightarrow123$
$\$693 − \$123 = \$570$
John’s new balance is approximately $\$570$.
5. Elsa is preparing for a spelling competition. If she learns 81 words per day, about how many words will she learn in 19 days?
Solution:
Number of words Elsa learns in $1$ day $= 81$
Number of words Elsa learns in $19$ days $= 81 \times 19$
To find the estimate we replace the numbers with compatible numbers.
$81 \rightarrow 80$ and $19 \rightarrow 20$
$80 \times 20 = 1600$
Elsa can learn around 1600 words in 19 days.
Practice Problems on Compatible Numbers
Compatible Numbers
Find the estimate of 167 + 35 using compatible numbers.
Estimating sum using compatible numbers as $167 + 33 = 200$.
In a charity show, $\$1289$ was collected on day 1 and $\$899$ was collected on day 2. Which of the following is the correct way to estimate the collection on both the days?
The correct way to estimate the collection on both days is $\$1300 + \$900$.
The monthly fee in an institute is $\$408$. Estimate the fee deposited by a student in 4 years.
4 years $= 4 \times 12 = 48$ months.
Estimating fee deposited by a student in 4 years as $\$400 \times 50 = \$20,000$.
A grocery store has 45,239 pounds of whole wheat in stock. If they sold out 39,782 pounds, approximately how much whole wheat is left in stock?
Estimating the weight of whole wheat left in stock as $45000 − 40000 = 5000$ pounds.
Estimate the quotient when 20,891 is divided by 687.
Estimating the quotient using compatible numbers as $21, 000 \div 700 = 30$.
Frequently Asked Questions on Compatible Numbers
Are friendly numbers also called compatible numbers?
Friendly numbers are also called compatible numbers. They are numbers that are easy to add, usually they have a sum of a multiple of ten. For example, 3 and 7 are friendly numbers that are also called compatible numbers.
Do compatible numbers always end in zeroes?
Compatible numbers are numbers that make the calculation easier. They need not always end in zeroes. 45 and 5 are also compatible numbers since adding them mentally is easy.
Which is a better method of estimation? Compatible numbers or rounding numbers?
Both are frequently used methods of estimation. The method to be chosen depends on the rate of accuracy of the estimation required.
Can we use compatible numbers to estimate fractions?
Yes, we can estimate fractions by replacing them with benchmark fractions that are common fractions that we can measure or judge against, when measuring, comparing, or ordering other fractions. Benchmark fractions are easy to visualize and identify, and thus, help in estimating the parts.
For example,
$\frac{5}{6} + \frac{1}{2}$
$\frac{5}{6}$ is close to 1 so it can be replaced with 1.
$1 + \frac{1}{2} = 1\frac{1}{2}$




































