- What Is the Perpendicular Bisector of a Chord?
- Properties of Perpendicular Bisector of a Chord
- Perpendicular Bisector of a Chord Theorem Proof
- Solved Examples on Perpendicular Bisector of a Chord
- Practice Problems on Perpendicular Bisector of a Chord
- Frequently Asked Questions about the Perpendicular Bisector of a Chord
What Is the Perpendicular Bisector of a Chord?
The perpendicular bisector of a chord is a line passing through the center of the circle such that it divides the chord into two equal parts and meets the chord at a right angle.
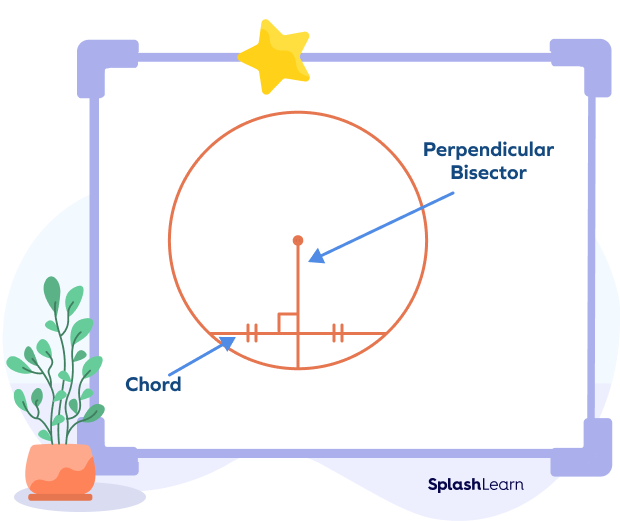
A circle is a 2D figure without corners or edges such that all the points on the boundary are equidistant from the center. The line segment connecting the center with any point on the circumference is called the radius.
A chord is a line segment that connects any two points on the circumference of the circle. The diameter of a circle is considered to be the longest chord of a circle.
Recommended Games
Properties of Perpendicular Bisector of a Chord
- A perpendicular bisector of a chord meets the chord at a right angle.
- A perpendicular bisector of a chord bisects the chord.
- A perpendicular bisector of a chord passes through the center of the circle.
If a line segment passing through the chord has any of these two properties, it also possesses the third.
- A line that is perpendicular to a chord and bisects it must pass through the center of the circle.
- A line that is perpendicular to a chord and passes through the center of the circle must bisect the chord.
- A line that bisects a chord and passes through the center of a circle must be perpendicular to the chord.
Perpendicular Bisector of a Chord Theorem
We can state the perpendicular chord bisector theorem in three ways.
Theorem 1: The line bisecting the chord while passing through the circle’s center is perpendicular to the chord.
Theorem 2: The line that is perpendicular to the chord and passes through the center of a circle bisects the chord.
Theorem 3: The perpendicular bisector of the chord will pass through the center of the circle. This is also called the perpendicular bisector of a chord conjecture.
Perpendicular Bisector of a Chord Theorem Proof
Theorem 1
Statement: The line that bisects the chord and passes through the center of a circle is perpendicular to the chord.
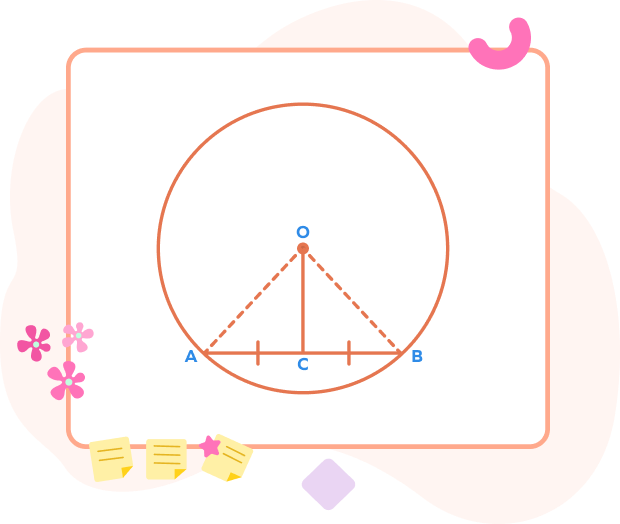
Proof:
Let the line segment OC bisects the chord AB and passes through the center O.
We have to prove that OC is perpendicular to AB.
| Statement | Reason |
|---|---|
| OA = OB AC = BC OC = OC $\Delta$OAC ≅ $\Delta$OBC ∠OCA = ∠OCB …(i) ∠OCA + ∠OCB $= 180^{\circ}$ …(ii) ∠OCA = ∠OCB $= 90^{\circ}$ OC$\bot$AB. Hence, proved. | OA and OB are radii of the circle. OC bisects the chord. Common side SSS congruence criterion CPCTC Angles on a straight line From (i) and (ii) |
Theorem 2
Statement: The line that is perpendicular to the chord and passes through the center of a circle bisects the chord.
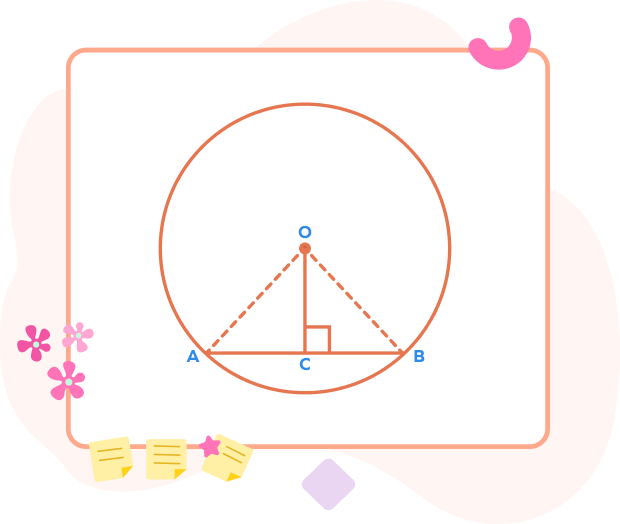
Proof:
OC passes through the center O. Let OC $\bot$ AB. We will prove that OC bisects AB. We need to prove that $AC = BC$.
| Statement | Reason |
|---|---|
| ∠OCA = ∠OCB $= 90^{\circ}$ OA = OB OC = OC $\Delta$OAC ≅ $\Delta$OBC AC = BC Hence, proved. | OC $\bot$ AB Radii of the same circle Common side RHS criterion CPCTC |
Theorem 3
Statement: The perpendicular bisector of any chord of a circle passes through the center of the circle.
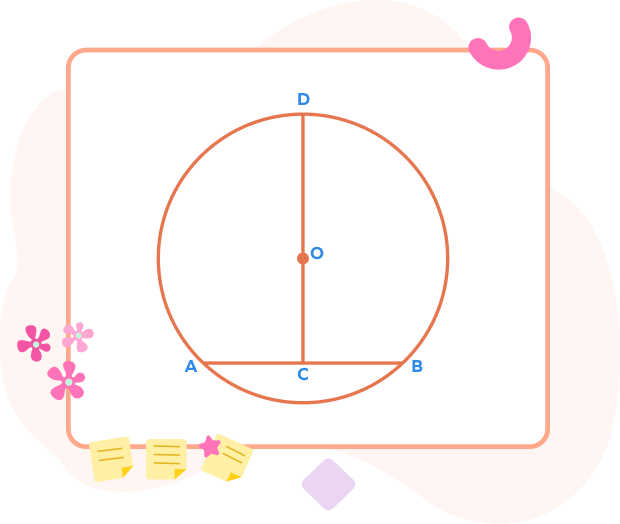
Proof:
Given that CD is a perpendicular bisector of chord AB.
C is the midpoint of AB.
∠DCA = ∠DCB $= 90^{\circ}$ …(i)
We have to prove that CD passes through the center O. Let’s assume that the line CD does not pass through the center O.
(Let’s imagine it as a different line as shown in the diagram below.)
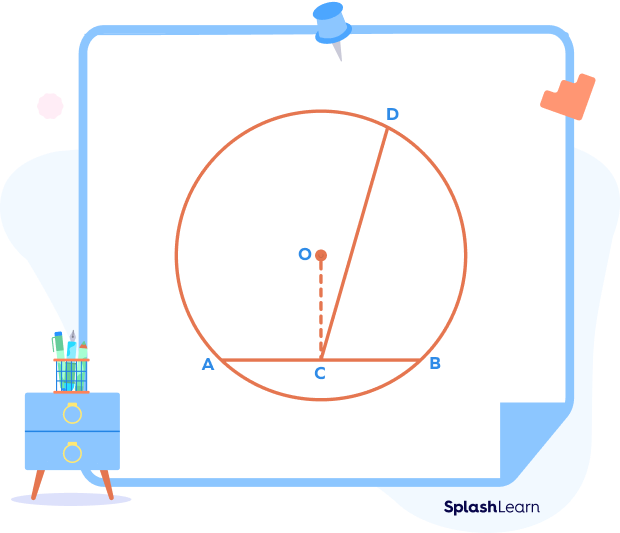
We know that a line that joins the center of a circle to the midpoint of a chord is always perpendicular to the chord. OC joins the center of a circle O to the midpoint C of a chord AB.
Thus, ∠OCA = ∠OCB $= 90^{\circ}$ …(ii)
This is a contradiction to (i).
Equations (i) and (ii) are possible only if C, O, and D lie on the same line.
Thus, the perpendicular bisector CD passes through the center O.
It proves that the perpendicular bisector of the chord will pass through the center of the circle.
Facts about Perpendicular Bisector of a Chord
- The diameter is the longest chord of a circle.
- The radius of a circle that is perpendicular to the chord bisects it.
Conclusion
In this article, we learned about the perpendicular bisector of a chord—a line that cuts a chord into two equal segments at right angles. Understanding this geometric concept and related theorems is vital in various applications, such as circle geometry and construction. Let’s now reinforce our knowledge with examples and MCQs for better comprehension.
Solved Examples on Perpendicular Bisector of a Chord
1. Find CM if the radius is 20 units and the length of the chord AB is 20 units.
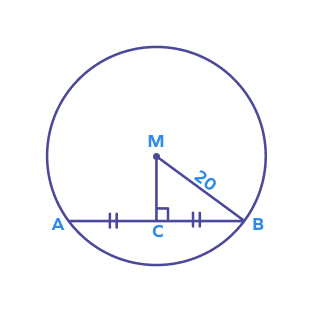
Solution:
According to the perpendicular bisector theorem, CM is the perpendicular bisector of AB.
$AC = BC = 10$ units
In the right triangle BCM, we have
BC2 + CM2 = BM2
202 = 102 + CM2
CM2 = = 300
CM = 17.3 units
2. O is the center of the circle. Find the missing length and the length of the chord AB.
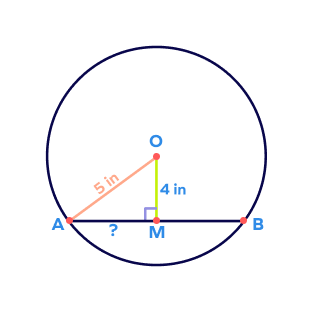
Solution:
OM passes through the center of the circle and it is perpendicular to the chord AB.
Thus, it is the perpendicular bisector of AB.
In right triangle OMA, we have
OA = 5 in, OM = 4 in
Thus, OM2 + AM2 = OA2
42 + AM2 = 52
AM2 = 25 – 16
AM2 = 9
AM = 3 in
Here, since OM is the perpendicular bisector, we have
AB = AM + BM = 3 + 3 = 6 in
3. What will be the length of the chord of the circle if radius is 15 units and the distance between the chord and center is 12 units?
Solution:
Use the Pythagoras theorem to find the length of the chord.
Hypotenuse = Radius of the circle
152 = 122 + Chord length2
225 = 144 + Chord length2
Chord length2 = 225 – 144
Chord length = $\sqrt{81}$
Chord length = 9 cm
4. Define the following terms: perpendicular bisector, chord and diameter.
Solution:
Perpendicular bisector: Perpendicular bisector of a segment is a line that meets the given segment at a right angle and divides the given segment into two equal parts.
Chord: Chord of a circle is a line segment that has its endpoints on the circumference of the circle.
Diameter: Diameter of a circle is a line segment that passes through the center of the circle such that its endpoints are on the circumference of the circle. It is the longest chord of the circle.
Practice Problems on Perpendicular Bisector of a Chord
Perpendicular Bisector of a Chord: Definition, Properties, Examples
The perpendicular bisector of the chord meets the chord at ________.
The perpendicular bisector of the chord meets the chord at a right angle.
If a line segment bisects the chord and passes through the center, then it is
A line that bisects a chord and passes through the center of a circle must be perpendicular to the chord.
What is the missing length?
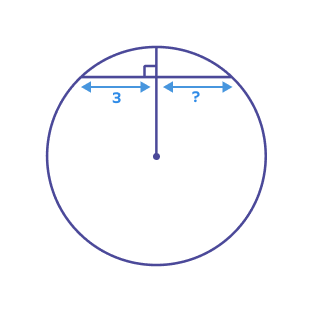
The line segment is the perpendicular bisector of the chord.
Thus, missing length $= 3$ units
The line segment that is perpendicular to the chord and passes through the center of the circle _______.
The line segment that is perpendicular to the chord and passes through the center of a circle bisects the chord.
Frequently Asked Questions about the Perpendicular Bisector of a Chord
What is the intersecting chord theorem?
The interesting chord theorem represents the intersection property of chords. It says that the product of the length of segments of one chord is equal to the product of the length of the segment of another chord.
What will be the properties of two parallel chords?
The two parallel chords in the circle will be at an equal distance from each other and their length will be the same.
What is the secant line of a circle?
The secant line of a circle is the extended form of the chord. It extends the circle beyond the points touching the circumference of the circle.
How do you find the perpendicular bisector of a chord?
A line that is perpendicular to the chord and passes through the center bisects the chord. Thus, to find the perpendicular bisector of a chord, draw a perpendicular to the chord from the center of a circle.
To find the length of the perpendicular bisector of a chord, we can use the Pythagoras theorem in a triangle, where the radius acts as the hypotenuse and the length of the perpendicular bisector acts as one of the legs.
What is the midpoint of the chord?
The midpoint of the chord is the point of intersection of the perpendicular bisector and chord. The fact that resultant segments are equal in length proves it to be the midpoint.

















