What Is the Point of Concurrency in Geometry?
The point of concurrency is the point where three or more lines intersect each other or pass through. In simple words, it is the point of intersection of three or more lines.
The word “concurrent” refers to events occurring simultaneously or at the same time. In 2D geometry, concurrent lines are the lines that precisely cross at one point. The intersecting lines are always concurrent.
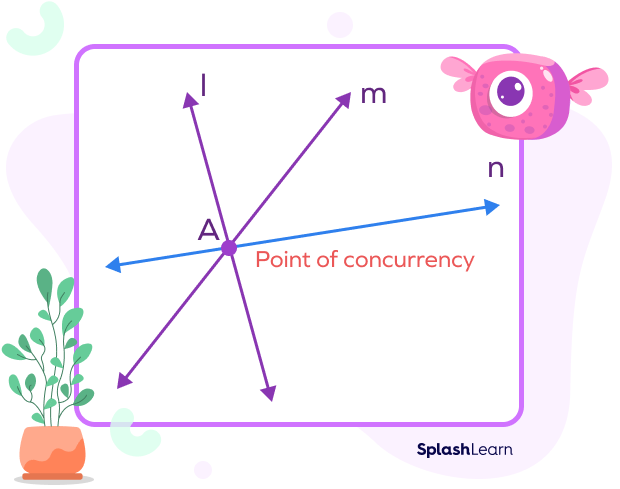
Lines l, m, and n intersect each other at point A. That means A is the point of concurrency. Lines l, m, and n are concurrent lines.
Recommended Games
Point of concurrency Definition in Geometry
In geometry, the point of concurrency refers to the single point where three or more lines, rays, or line segments intersect or come together simultaneously.
Recommended Worksheets
Concurrency Points in Triangles
In a triangle, special types of lines can be drawn, such as altitudes, medians, angle bisectors, or perpendicular bisectors.
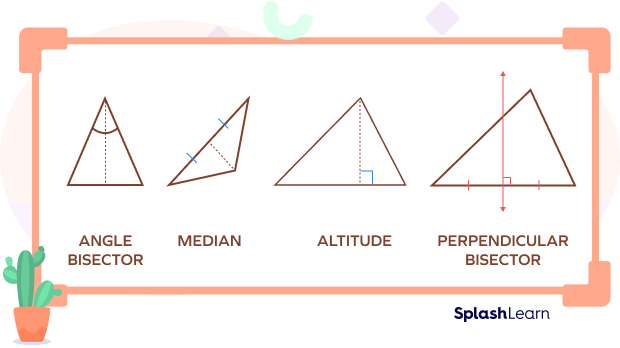
- Altitudes: These are the perpendicular lines drawn from the vertices of the triangle to the opposite side. A triangle has three altitudes whose point of concurrency is called orthocenter.
- Medians: These line segments are drawn from the vertices of the triangle to the midpoint of the opposite side. A triangle has three medians whose point of concurrency is known as the centroid of a triangle.
- Angle bisectors: These lines bisect the angles of the triangle. A triangle has three angle-bisectors (one for each angle) whose point of concurrency is incenter.
- Perpendicular bisectors: These are the lines that bisect the sides of the triangle at a right angle. A triangle has three perpendicular bisectors whose point of concurrency is called the circumcenter.
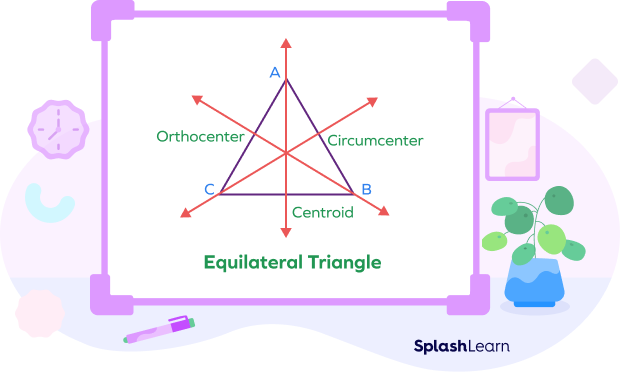
Only an equilateral triangle has the centroid, circumcenter, incenter, and orthocenter at the same point!
How to Find Points Of Concurrency
- The point at which three or more lines intersect is the point of concurrency.
- In a triangle, for each type of line segment (altitudes, medians, angle bisectors, or perpendicular bisectors), the point of concurrency has a special name. Let’s find out.
Different Points of Concurrency in a Triangle
The different concurrent points in the triangle are referred to as different centers according to the lines meeting at that point.
There are four different concurrency points in a triangle:
- Centroid: The point of intersection of medians
- Circumcenter: The point of intersection of perpendicular bisectors
- Incenter: The point of intersection of angle bisectors
- Orthocenter: The point of intersection of altitudes
Let’s discuss each point in detail.
Centroid: Point of Concurrency of Medians
It is a point in the plane figure that can be found away from the average of all the points.
The centroid of a triangle is a point at which the medians of a triangle coincide. In other words, we can say that when three medians of a triangle intersect at a common point, this creates the centroid. And the point of intersection is known as the point of concurrency of medians.
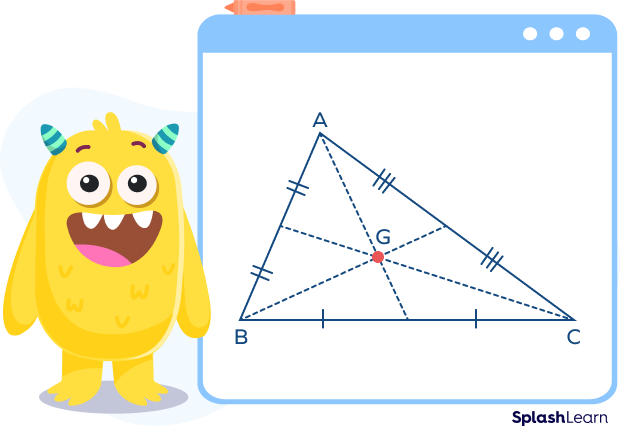
- In the above figure point G is called the centroid of the triangle ABC.
- The centroid of a triangle intersects all three medians of a triangle in the ratio 2:1.
- It always lies within the triangle.
Circumcenter: Point of Concurrency of Perpendicular Bisectors
The point of concurrency of all the perpendicular bisectors of all sides of a triangle is known as the circumcenter.
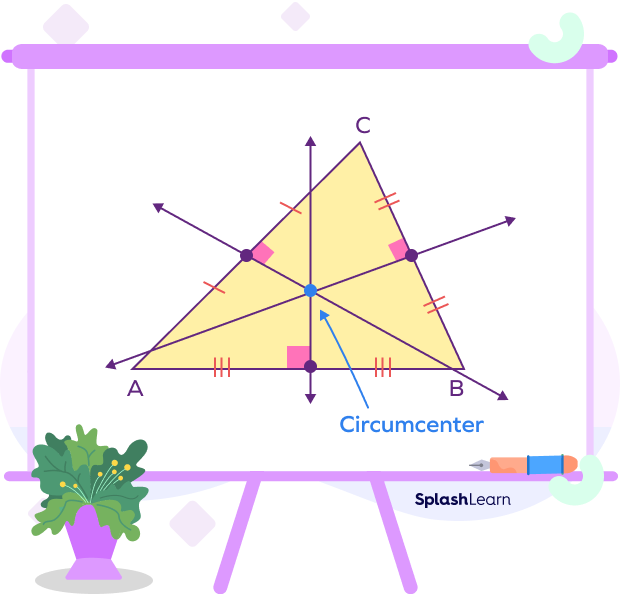
- The circumcenter is the point that is equidistant from all the vertices of the triangle.
- With a circumcenter as its center, a circle known as a circumcircle can be drawn by touching the vertices of the triangle.
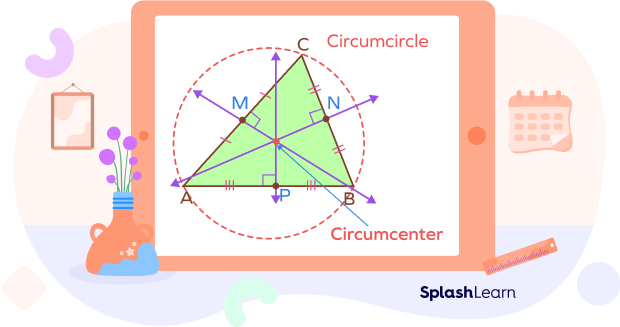
- The circumcenter of an obtuse-angled triangle is outside the triangle.
- For a right-angled triangle, the circumcenter lies at the hypotenuse.
Incenter: Point of Concurrency of Angle Bisectors
The intersection of the angle bisectors of all the interior angles of the triangle is known as the incenter.
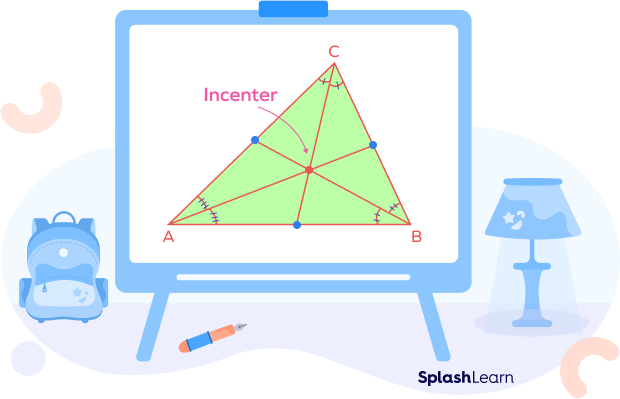
- With the incenter as the center, a circle drawn by touching all sides internally is known as an incircle.
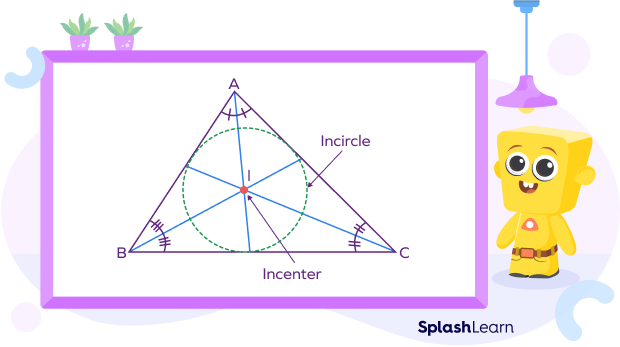
- The incenter is the point that is equidistant from the sides of the triangle.
- The incenter always lies within the triangle.
Orthocenter: Point of Concurrency of Altitudes
The point of intersection of the three altitudes is known as the orthocenter.
- It may lie outside of the triangle.
- For an obtuse-angled triangle, the orthocenter lies outside the triangle.
- For any right triangle, the orthocenter is at the vertex of the right angle.
Facts about Points of Concurrency
- A triangle’s centroid will always fall between the triangle’s orthocenter and circumcenter.
- The distance from the centroid to the circumcenter is always half the distance between the centroid and orthocenter.
- For every right triangle, the circumcenter is always the midpoint of the hypotenuse.
- All four points of concurrency (centroid, circumcenter, incenter, and orthocenter) can be concurrent in itself.
Conclusion
In this article, we have covered points of concurrency, different points of concurrency in the triangle, and important facts to know about the point of concurrency. Let us now look at some solved examples and frequently asked questions to understand the concept better.
Solved Examples on Point of Concurrency
- In the figure given below, what is point P called?
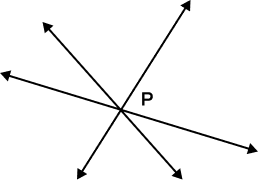
Solution:
In the given figure, all three lines intersect at point P.
The point P is the point of intersection of three lines.
Hence, P is called the point of concurrency. Three lines are called concurrent lines.
- In the figure given below, if I represents the incenter of the triangle, then find the measure of angle ∠ABN.
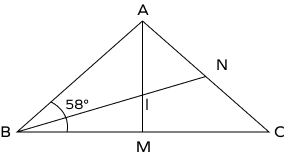
Solution:
We know that the incenter of a triangle is formed by the angle bisectors of a triangle.
In the given figure, BN is an angle bisector of angle ∠ABC.
Hence, ∠ABN=∠ABC2=5802=290.
- An equilateral triangle ABC as shown in the figure has each side length of 12 feet.
(i) Name the point P (ii) Find ∠ABP (iii) Name the line AD, BE, and CF. (iv) Find the length of AE.
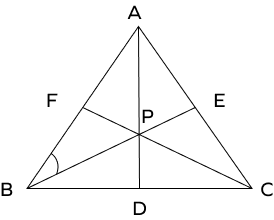
Solution:
(i) In the figure, point P is the point of concurrency of all three medians, altitudes, perpendicular bisectors, and angle bisectors. In an equilateral triangle, the centroid, circumcenter, orthocenter, incenter are represented by the same point.
(ii) The line segment BE is the angle bisector of angle ∠ABC.
In an equilateral triangle, each interior angle measures 600.
Hence, ∠ABP =∠ABC2 = 6002 = 300.
(iii) The lines AD, BE, and CF are concurrent lines. In equilateral triangles medians, altitudes, perpendicular bisectors, and angle bisectors all coincide. Hence the line AD, BE, and CF can be medians or altitudes or perpendicular bisectors, or angle bisectors.
(iv) Length of AE = AC2 = 122 = 6 feet.
Practice Problems on Point of Concurrency
Point of Concurrency
The centroid of a triangle divides the median in the ratio______.
The centroid of a triangle divides the median in the ratio of 2:1.
The point of concurrency of the angle bisectors of all the interior angles of the triangle is known as the______.
The point of concurrency of the angle bisectors of all the interior angles of the triangle is known as the incenter.
What is the name of the circle passing through all the vertices of a triangle?
The circle passing through all the vertices of a triangle is known as the circumcircle.
Where does the incenter of any triangle lie?
The incenter of any triangle always lies inside the triangle.
Point of concurrency of _____ is known as an orthocenter of the triangle.
The point of concurrency of altitudes is known as an orthocenter of the triangle.
Frequently Asked Questions about Point of Concurrency
What are the different points of concurrency?
The four major points of concurrency are centroid, circumcenter, incenter, and orthocenter.
How many points of concurrency coincide in an equilateral triangle?
In an equilateral triangle, four points of concurrency (centroid, circumcenter, incenter, and orthocenter) coincide.
Which triangle’s circumcenter lies at the hypotenuse?
A right-angled triangle’s circumcenter lies at the hypotenuse.
Which type of triangle has the orthocenter lying outside it?
An obtuse-angled triangle has an orthocenter that lies outside the triangle.



























