What Is Polynomial in Standard Form?
The standard form of a polynomial or a polynomial in the standard form refers to a polynomial whose terms are written in the descending order of the degree of the variables (highest to lowest).
| Example of standard form of a polynomial | Non-example of standard form of a polynomial |
|---|---|
| $2x^{2} + 5x\;-\;1$ | $5x\;-\;1 + 2x^{2}$ |
In the standard form, the highest degree term is placed at the beginning of the polynomial followed by other terms in the decreasing order of degree. Terms are in the decreasing exponential value.
Recommended Games
Meaning of Polynomial in Standard Form
The terms of the polynomial in standard form are organized from highest degree to lowest degree, which helps in simplifying and performing various operations on polynomials.
A polynomial is said to be in its standard form if it is written in such a way that the term with the highest degree is placed at the beginning, followed by the term having the next highest degree, and so on. In other words, the degree of terms decreases as you go from left to right.
Example: $x^{7} + 5x^{6}\;-\;2x^{5} + 5x^{4} + x^{3}\;-\;3x^{2} + 9x + 2$
Recommended Worksheets
Polynomial in Standard Form Definition
Standard form of a polynomial is a way of writing a polynomial where the terms are arranged in descending order of degree. A polynomial in standard form is a polynomial written such that its exponents are in descending order.
The standard form of a polynomial with degree n is given by
$a_{n}x^{n} + a_{n-1}x^{n-1} +$ . . .$+ a_{1}x + a_{0}$
(Note: The first term of a polynomial in standard form, the term containing the highest degree, is called the leading term.)
Standard Form of Polynomial – Degree
When the polynomial is written in the standard form, the degree of the polynomial is simply the degree of the first term.
| Polynomial in the standard form | Degree |
|---|---|
| $3x^{3}\;-\;2x + 1$ | 3 |
| $x^{2}\;y^{3}\;-\;2xy + x$ | 5 |
The degree of a polynomial with a single variable can be defined as the highest exponent of the variable present in the variable. In the polynomial constituting multiple variables, the degree is calculated by finding the sum of the exponents of variables in each term and then comparing to find the highest degree.

How to Write a Polynomial in Standard Form
Let’s understand the steps to convert a polynomial to standard form.
Step 1: Add or subtract the like terms (if any) to identify the total number of terms present in the polynomial. Note down the degree of each term.
Step 2: Write the term with the highest degree in the beginning.
Step 3: Arrange the terms in descending order of the degree. Do not forget to take along the signs attached to each term. Place the mathematical operators carefully.
Step 4: The constant or 0-degree term will come in the end.
Addition and Subtraction of Standard Form of Polynomial
Writing polynomials in standard form helps us to identify the like terms in the given polynomials, which makes the addition or subtraction of polynomials much easier.
Two or more terms are called like terms if they have the same variable (or variables) with the same exponent. The important rule when adding or subtracting polynomial expressions is, we can only add or subtract like terms.
Example: $\;-\;4x^{3}\;y$ and $6x^{3}\;y$ are like terms.
Steps for the Addition of Polynomials
Step 1: Write the polynomials in standard form.
Step 2: Write both the polynomials vertically to align the like terms (in case of no extra term). The polynomials can also be added horizontally, where like terms must be grouped for ease of calculation.
Step 3: Perform the addition according to the signs.
| Vertical addition | Horizontal addition |
|---|---|
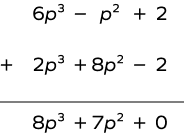 | $(6p^{3} \;-\; p^{2} + 2) + (2p^{3} + 8p^{2} \;-\; 2)$ $= 6p^{3} + 2p^{3} + 8p^{2}\;-\; p^{2} \;-\; 2 + 2$ $= 8p^{3} + 7p^{2}$ |
Steps for the Subtraction of Polynomials
Step 1: Write the polynomial in standard form.
Step 2: Write the polynomials vertically (one below the other) such that terms are aligned. You can also write them horizontally and group the like terms.
Step 3: To subtract, reverse the sign of each term in the second polynomial and add the two polynomials. Follow the sign convention while adding.
| Vertical Subtraction | Horizontal subtraction |
|---|---|
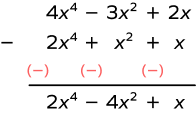 | $4x^{4} \;-\; 3x^{2} + 2x \;-\; (2x^{4} + x^{2} + x)$ $= 4x^{4} \;-\; 3x^{2} + 2x \;-\; 2x^{4} \;-\; x^{2} \;-\; x$ $= 4x^{4} \;-\; 2x^{4} \;-\; 3x^{2} \;-\; x^{2} + 2x \;-\; x$ $=2x^{4} \;-\; 4x^{2} + x$ |
Facts about Polynomials in Standard Form
- The standard form of every polynomial is unique and specific for that polynomial.
- The degree of the polynomial written in the standard form is the degree of the first term (leading term).
- The first term in the standard form of polynomial is called the leading term and its coefficient is called the leading coefficient.
- To simplify a polynomial in the standard form, combine like terms for addition/subtraction, and rearrange the terms in descending order of degree.
Conclusion
In this article, we learned about the standard form of a polynomial. Let’s solve a few examples and practice problems for better understanding and clarity.
Solved Examples on Polynomials in Standard Form
1. Convert the polynomial to standard form: $\;-\;3x^{2} + x^{4}\;-\; 5x + 5x^{3}+ 1$.
Solution: There are 5 terms.
Degree of $3x^{2} = 2$
Degree of $x^{4} = 4$
Degree of $5x = 1$
Degree of $5x^{3} = 3$
Degree of $1 = 0$
A polynomial in standard form is written by arranging terms in the descending order of the degree.
Polynomial in the standard form: $x^{4} + 5x^{3}\;-\; 3x^{2} \;-\;5x +1 = 0$.
2. What is the degree of a polynomial $5x^{3} + xy^{4} \;-\; 3xy^{2} \;-\; 4$? Write it in the standard form.
Solution:
The degree of the polynomial will be calculated for each term as follows:
| Term | $xy^{4}$ | $3xy^{2}$ | $5x^{3}$ | 4 |
| Degree | $1 + 4 = 5$ | $1 + 2 = 3$ | 3 | 0 |
In the standard form, we can write the given polynomial as
$xy^{4} + 5x^{3}\;-\; 3xy^{2} \;-\; 4$
The term xy4 has the highest sum of exponents. Thus, the degree of the polynomial is 5.
3. Add the following polynomials: $p(x) = 3x^{2} + 2x^{3} \;-\; 5$ and $q(x) = 12x^{2} + 3x^{3} \;- \;1$.
Solution:
Rewrite the polynomials in the standard form.
$p(x) = 2x^{3} + 3x^{2} \;-\; 5$
$q(x) = 3x^{3} +12x^{2} \;-\; 1$
$p(x) + q(x) = (2x^{3} + 3x^{2} \;-\; 5) + (3x^{3} + 12x^{2}\;-\; 1)$
$p(x) + q(x) = 5x^{3} + 15x^{2} \;-\; 6$
Practice Problems on Polynomials in Standard Form
Polynomial in Standard Form - Definition, Solved Examples, Facts, FAQs
Which terms in polynomials do not contain variables?
Constant term does not contain variables.
Which polynomial is in the standard form?
$\;-\;15x^{5} + 12x^{3}$ is written using the descending order of the exponents.
What is the degree of the polynomial: $\;-\;18x^{5} + 3x^{3} + 2x^{2}$?
Highest power of a variable is 5.
The degree of the polynomial in the standard form is the
The degree of the polynomial in the standard form is the degree of the leading term.
Which polynomials are in standard form?
The highest degree term must be placed first, followed by the lower degree terms.
Frequently Asked Questions on Polynomials in Standard Form
Can variables in polynomials have fractional or negative exponents?
No. Exponents of the variables in polynomials cannot be fractional or negative. Coefficients of variables can be fractions.
Can polynomials have an infinite number of terms?
A polynomial cannot have an infinite number of terms.
How to write the standard form of a polynomial having two variables?
Find the degree of each term by adding exponents of the variables. Arrange the terms by the descending order of the degree.
What is a homogeneous polynomial?
When each term of the polynomial (each monomial) has the same degree, it is a homogeneous polynomial.




































