What is Descending Order?
Ordering simply means the arrangement of objects based on certain rules. Descending order of numbers refers to arranging numbers in decreasing order, from the largest to the smallest.

Descending Order: Definition
The arrangement of information (like numbers, quantities, lengths, etc.) from the largest value to the smallest value is known as descending order.
Let’s look at some examples:

We can arrange these numbers in decreasing order of their value.

Descending can also be thought of as climbing down the stairs of numbers starting from the highest value.

Moving down the slide is also referred to as descending. Isn’t this an easy way to remember the meaning of descending order?

The following image shows how to arrange objects in decreasing order of their height, from the biggest to the smallest.
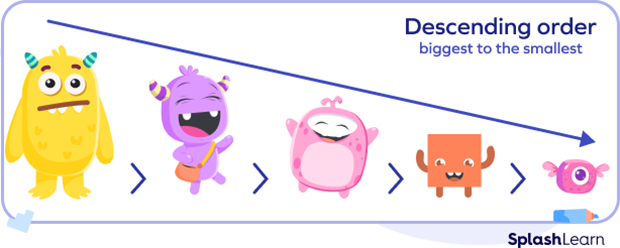
Fun Facts!
- The numbers on a number line are always arranged in increasing or ascending order (see the direction of the arrow).
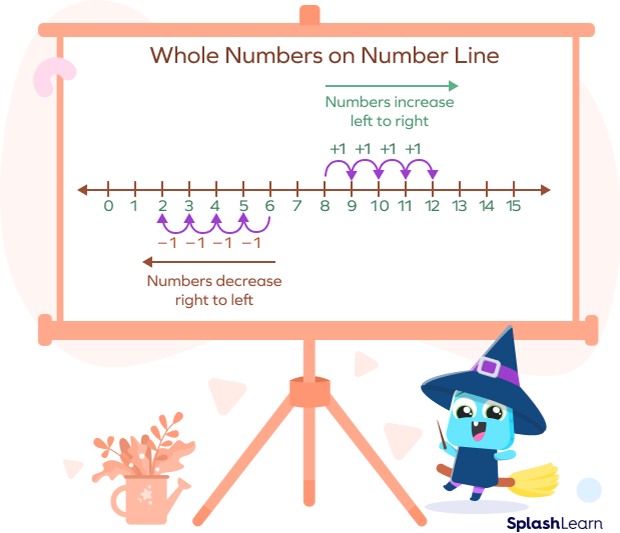
- Backward counting is counting in descending order.
Recommended Games
Symbol for Descending Order
Descending order always goes from the largest value to the smallest value. The greater-than symbol “$\gt$” is used to write numbers in descending order. The pointed end faces the smaller number, and the open end faces the bigger number.
Example 1: Arrange 3, 5, 7, 2, 6, and 8 in decreasing order.
When you arrange these numbers in descending order, the symbol is placed in the following way: $8 \gt 7 \gt 6 \gt 5 \gt 3 \gt 2$.
Example 2: Arrange in decreasing order: $\;-\; 5, \;-\;9, \;-\;10, \;-\;2, \;-\;3, \;-\;7$
The numbers can be written in the decreasing order as
$\;-\;2 \gt \;-\;3 \gt \;-\;5 \gt \;-\;7 \gt \;-\;9 \gt \;-\;10$

Recommended Worksheets
Alphabets in Descending Order
The descending order in the alphabet will go from Z to A.
As a result, the letters can be arranged in decreasing order using the following notation:

Example: Arrange the following words in descending order of their first letter.
ALGEBRA, GEOMETRY, TRIGONOMETRY, MATHEMATICS
Descending order of the first letter: T, M, G, A
Descending order: TRIGONOMETRY, MATHEMATICS, GEOMETRY, ALGEBRA
Descending Order of Fractions
Like Fractions
Like fractions are fractions that share the same denominator. To compare like fractions or to arrange like fractions in descending order, we simply arrange their numerators in descending order.
Example: $\frac{1}{4}, \frac{5}{4}, \frac{3}{4}$, and $\frac{7}{4}$ are like fractions, as shown in the image below.
They can be arranged in descending order as $\frac{7}{4} \gt \frac{5}{4} \gt \frac{3}{4} \gt \frac{1}{4}$, as their numerators are written in descending order as $7 \gt 5 \gt 3 \gt 1$.
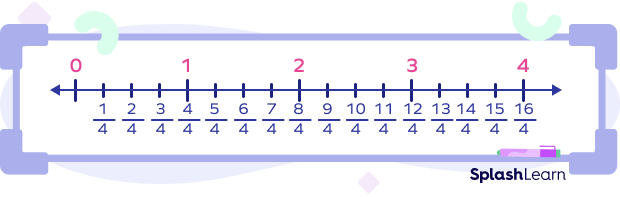
Unlike Fractions
Unlike fractions are fractions that don’t share the same denominator and instead have different denominators. To organize unlike fractions in descending order, you have to convert them to like fractions and then compare their numerators.
Once the denominator of all fractions becomes the same, the fraction with the largest numerator is considered the highest, and the fraction with the smallest numerator is the lowest.
For example, $\frac{3}{4}, \frac{5}{2}$, and $\frac{6}{7}$ are unlike fractions.
Firstly, you convert them into like fractions by taking the LCM of their denominators.
LCM of 4, 2, and 7 is 28.
So, after making the denominators the same, these fractions become $\frac{21}{28},\; \frac{70}{28}$, and $\frac{24}{28}$ respectively.
By comparing their numerators, they can now be arranged in descending order as
$\frac{70}{28} \gt \frac{24}{28} \gt \frac{21}{28}$
or $\frac{5}{2} \gt \frac{6}{7} \gt \frac{3}{4}$
Descending Order of Decimals
To arrange the decimals in descending order, you have to look at the position of digits from left to right (from the highest place value to the lowest) as per the place value of decimal numbers. So, compare the whole number part first. If it matches, we move to the decimal part.

Example 1) $3.45 \gt 2.71$ since $3 \gt 2$.
Example 2) $4.12 \gt 4.03$ since $1 \gt 0$.
Example 3) 1.50, 0.7, 0.2, 0.45, 0.95 can be arranged in descending order as,
$1.50 \gt 0.95 \gt 0.7 \gt 0.45 \gt 0.2$.
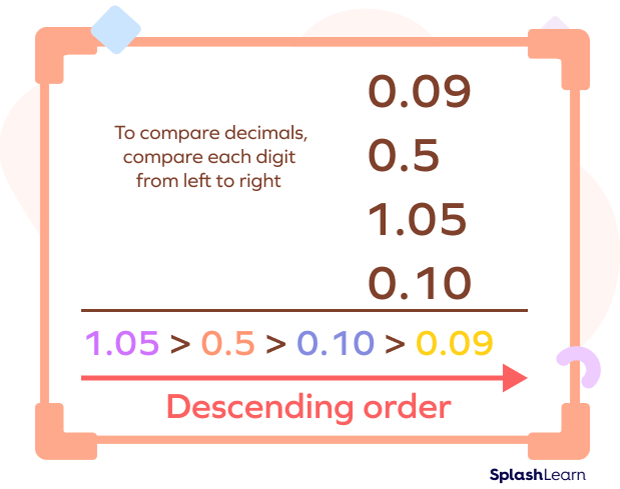
Facts about Descending Order
The opposite of descending order is the ascending order. Ascending order or decreasing order is the arrangement of things (numbers, quantities) from the lowest value to the highest value. Thus, it is the exact opposite process of descending order.
Conclusion
Descending order is, simply put, an arrangement of data from highest to lowest value. This data can comprise numbers, integers, fractions, decimals, money, etc. Knowing descending order is essential as it helps you sort things in order of greatest to smallest based on their numeric values, figures, and importance.
Solved Examples on Descending Order
1. Sort the following numbers in descending order:
97, 101, 45, 83, 59, 32, 111, 90, 09, 14
Solution:
To sort in descending order, we place the numbers from largest to smallest as shown below:
111, 101, 97, 90, 83, 59, 45, 32, 14, 09.
2. Four friends, Jack, Rick, Lilly, and Ellen, saved some money—$\$110$, $\$450$, $\$80$, and $\$216$, respectively—in their piggy banks. Which friend has the most amount of money saved? Place these amounts in descending order.
Solution:
Rick has the most amount of money saved, i.e., $\$450$.
The amount of money from the highest to lowest order is:
$\$450$, $\$216$, $\$110$, $\$80$.
3. List the following dates in descending order:
January 3, 2008, December 26, 2019, May 1, 2008, August 13, 2022, July 4, 2000.
Solution:
To arrange the dates in descending order, we first check the years, then the months, and then the days.
Based on this, we list the dates in descending order as follows:
August 13, 2022, December 26, 2019, May 1, 2008, January 3, 2008, July 4, 2000.
4. Arrange the given fractions in descending order:
$\frac{2}{5}, \frac{4}{6}, \frac{7}{9}, \frac{1}{2}, \frac{5}{6}$, 1.
Solution:
Since the fractions are unlike, first, we find the LCM of their denominators.
LCM (5, 6, 9, 2, 1) = 90.
Then, we convert the unlike fractions into like fractions:
$\frac{36}{90}, \frac{60}{90}, \frac{70}{90}, \frac{45}{90}, \frac{75}{90}, \frac{90}{90}$
Now, we arrange the like fractions in descending order based on their numerators:
$\frac{90}{90} \gt \frac{75}{90} \gt \frac{70}{90} \gt \frac{60}{90} \gt \frac{45}{90}\gt \frac{36}{90}$.
Therefore, the final order becomes as follows: $1, \frac{5}{6}, \frac{7}{9}, \frac{4}{6}, \frac{1}{2}, \frac{2}{5}$.
5. Sort these decimals in descending order:
10.13, 56.78, 32.19, 56.76, 31.11, 101.5
Solution: The decimal numbers can be sorted in descending order using their place values as follows:
$101.5 \gt 56.78 \gt 56.76 \gt 32.19 \gt 10.13$.
6. List the following dates in descending order:
12/20/2015, 09/13/2008, 12/25/2022, 05/05/2031Solution: We check the years and arrange the dates in descending order in the following manner: 05/05/2031, 12/25/2022, 12/20/2015, 09/13/2008.
Practice Problems on Descending Order
Descending Order - Definition with Examples
Arrange the given numbers in descending order: $-66, \;-121, \;-95, \;-23, \;-79, \;-52$
As we go from right to left on a number line, the numbers decrease. Upon comparing the values of numbers from highest to lowest, we get $-23 \gt -52 \gt -66 \gt -79 \gt -95 \gt -121$.
Arrange the given fractions in descending order: $\frac{3}{6}, \frac{4}{6}, \frac{7}{6}, \frac{2}{6}, \frac{5}{6}$
The given fractions are like fractions since they have the same denominator, 6. Upon comparing their numerators, we will get option d) as the answer.
Arrange the following numbers in descending order: 50.3, 50.13, 50.05, 50.55, 50.8
We examine the digits starting from the first digits on the right side of the decimal and find option b) as the answer.
Arrange the money in descending order: $\$250, \$58, \$175, \$313$
We compare the monetary values and arrange them in descending order to get the correct answer, i.e., option d).
Frequently Asked Questions on Descending Order
What is another name for descending order?
Descending order is also called decreasing or declining order.
Why is descending order important?
Descending order is important because it helps classify data from the most important to the least important item or from the highest value to the lowest value. For example, it can help you compare prices of items by arranging them from their highest to lowest price.
What are the rules of descending order?
- Always start with the largest number.
- Always ensure that the numbers are in order from largest to smallest.
- Always end with the smallest number.
What is the difference between ascending and descending order?
Ascending order is the one in which the numbers are organized from the lower value to the higher value. It is the reverse of descending order, in which numbers are organized from higher to lower values.




































