Radius of a Circle – Definition, Formula, Facts, Examples, FAQs

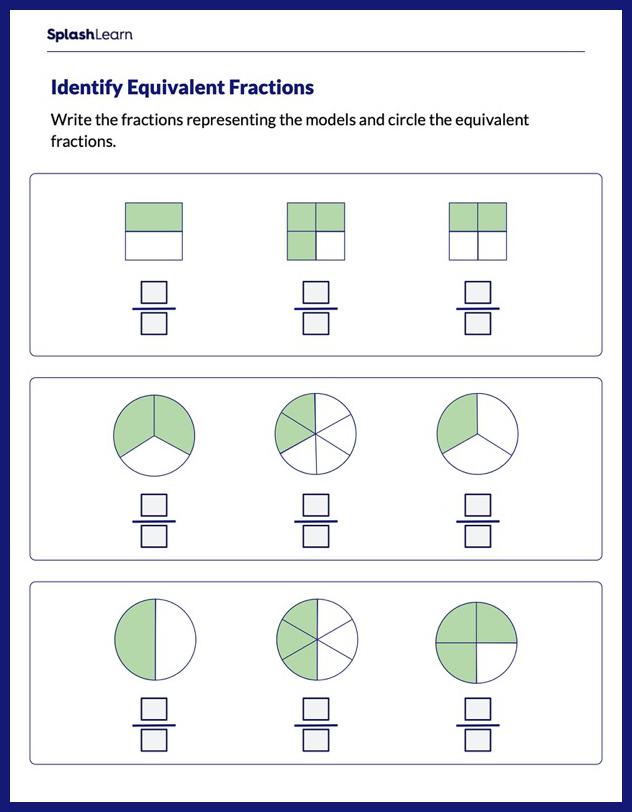
What Is the Radius of a Circle?

The radius of a circle represents the distance between the center and the boundary of the circle (circumference). The radius is generally denoted by “R” or “r.”

The word “radius” is the singular form, while “radii” is the plural form. 

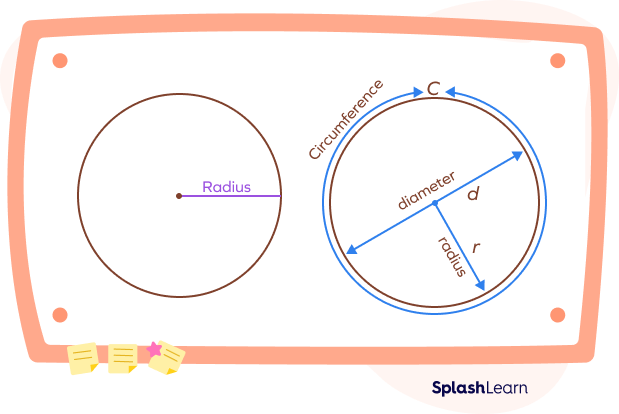
Note that 3D shapes such as spheres, cylinders, cones, shapes with circular bases also have a radius.

Radius of a Circle: Definition

The measure of distance between the center of a circle and any point on the boundary of the circle is called its radius. 

Radius of a Circle: Formulas

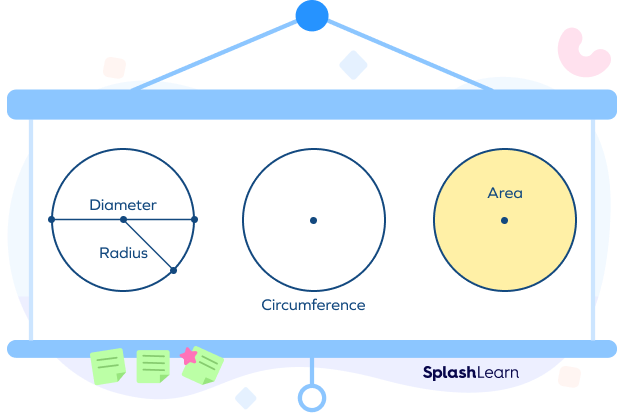
We can express radius in terms of diameter, circumference, or area of a circle. Before we go into that, let’s quickly look into what these terms represent.  

Radius Formula from Diameter

Diameter is the length of a line segment passing through the center of the circle and connecting any two points on the circumference (boundary).  Half of the diameter is the radius.

Diameter $= 2 \times Radius$

Radius $= \frac{Diameter}{2}$

r $= \frac{d}{2}$

Radius Formula from Circumference

Circumference is the total distance of the boundary of the circle given by 2r.

Circumference $= C = 2\pi r$

$r = \frac{C}{2\pi}$

Radius Formula from Area

The space or region enclosed within the circumference of the circle is its area.

Area of a circle $= \pi r^{2}$

Radius = $\sqrt{\frac{Area}{\pi}}$

Equation of a Circle with Radius r

The equation of a circle having radius r and center at origin (0, 0) is given by

$x^{2} + y^{2} = r^{2}$ 

Equation of a circle having radius r and with center (h, k) is given by

$(x\;-\;h)^{2} + (y\;-\;k)^{2} = r^{2}$

Facts about Radius of a Circle

Conclusion

A circle is a very common shape found numerous times in our day-to-day life. Beginning from glasses and sunlight, to ending the day with the moon and clock, there are multiple circles. Thus, knowing the formula for its measurement is necessary. The radius of the circle is the distance from the center to the circumference. It is related to the diameter and area of the circle as well. 

Solved Examples on Radius of Circle

1. A wire measures 10 units in length. Find the radius of a circle formed by bending the wire and joining its two ends? (Use $\pi = 3.14$).

Solution: 

A circle is made by bending the wire of length 10 units. Thus, the circumference of the circle is 10 units. 

C $= 2\pi r$

$10 = 2r\pi $

Radius $= r = \frac{10}{2\pi}$

Radius $= r = \frac{10}{2\pi}$

Radius $= r = 1.6$ units

2. What is the radius of the given circle? 

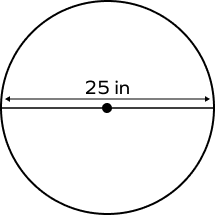
Solution: 

The given line segment is the diameter of the circle.

Diameter = 25 in

Radius $= \frac{Diameter}{2}$

Radius $= \frac{25}{2}$

Radius = 12.5 in

3. A circular garden spans a region of 50.24 square feet. Find the radius.

Solution: The area of a circle is given by

Area $= \pi r^{2}$

To calculate the radius, rearrange the equation in terms of radius. 

Radius  $= \sqrt{\frac{Area}{\pi}}$

Radius $= \sqrt{\frac{50.24}{3.14}}$

Radius $= \sqrt{\frac{50.24}{3.14}}$

Radius $= \sqrt{16}$

Radius = 4 feet

5. What is the radius of a circle with its center at origin, if (2, 4) is a point on the circumference of a circle?

Solution: 

The equation for the radius of the circle with radius r and center (0, 0) is $x^{2} + y^{2} = r^{2}$.

The (2, 4) point lies on the circle, so it satisfies the equation of the circle.

$2^{2} + 4^{2} = r^{2}$

$r^{2} = 4 + 16$

$r^{2} = 20$ 

$r = \sqrt{20}$

r = 4.5 units

Practice Problems on Radius of Circle

Frequently Asked Questions about Radius