Reciprocal of a Fraction – Definition, Steps, Examples, FAQs

What Is the Reciprocal of a Fraction?

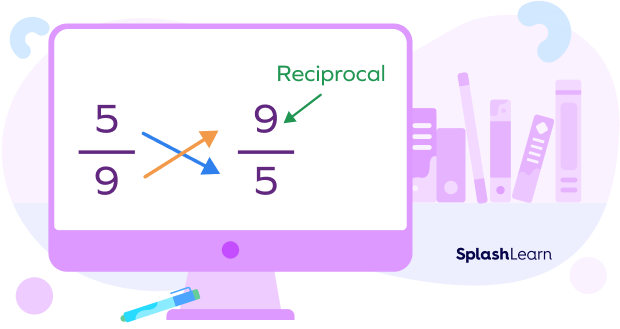
The reciprocal of a fraction is obtained by interchanging the numerator and the denominator. It represents the multiplicative inverse of the given fraction. 

A reciprocal of any non-zero number is simply written as 1 divided by that number.

The reciprocal of a fraction is a value which, when multiplied with the given fraction, results in 1.

Examples of Reciprocal of Fractions:

• The reciprocal of $\frac{1}{2}$ is $\frac{2}{1}$ or simply 2.
• The reciprocal of $\frac{3}{4}$ is $\frac{4}{3}$.

Reciprocal of a Fraction Definition

The reciprocal of a fraction is a multiplicative inverse of the original fraction. It is a new fraction that is obtained by interchanging the numerator and the denominator of the original fraction.

How to Find the Reciprocal of a Fraction

Finding reciprocal of fractions is simple. We only need to interchange or swap the numerator and denominator in order to determine the reciprocal of a fraction. 

In general, reciprocal of a fraction $\frac{a}{b}$ is written as$\frac{b}{a}$. (a, b are whole numbers, $a \neq 0$, $b \neq 0$)

For example, the reciprocal of $\frac{5}{11}$ is $\frac{11}{5}$.

Note: You can also find the reciprocal of a fraction by dividing 1 by the fraction.

Reciprocal of 0

The reciprocal of 0 is not defined. There is no value or number which, when multiplied with 0, results in 1. Thus, 10 is undefined.

Reciprocal of a Fraction Visualization

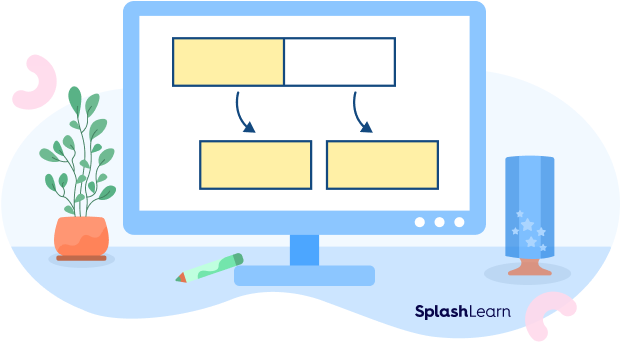
We know that the reciprocal of $\frac{1}{2}$ is 2. 

How many halves make 1 whole?

Two halves make 1 whole.

Two $\frac{1}{2}$ parts make 1 whole.

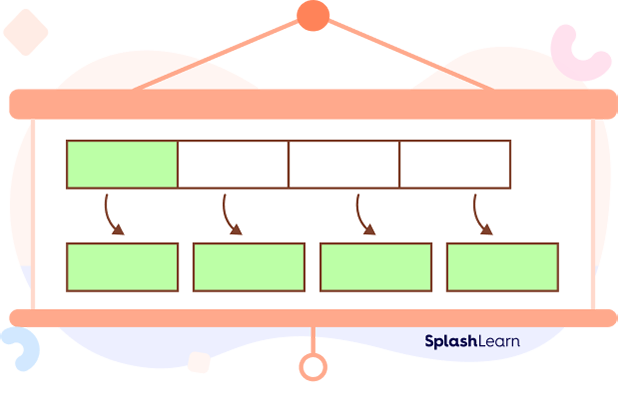
Similarly, the reciprocal of $\frac{1}{4}$ is 4.

How many quarters $(\frac{1}{4})$ make 1 whole?

Four $\frac{1}{4}$ parts can fit in 1 whole.

Reciprocal of a Mixed Fraction

To find the reciprocal of a mixed fraction, we first need to convert it to an improper fraction. An improper fraction has a numerator that is greater than or equal to the denominator. After getting the improper fraction, we can take its reciprocal by interchanging the numerator and denominator.

Example: Consider a mixed fraction $4\frac{5}{7}$. 

To convert it to an improper fraction, we multiply the whole number (4) by the denominator (7) and add the numerator (5). This value is the numerator. Denominator stays the same.

$4\frac{5}{7} = \frac{(7 × 4) + 5}{7} = \frac{33}{7}$ 

Therefore, the improper fraction for the mixed fraction $4\frac{5}{7}$ is $\frac{33}{7}$.

Now, the reciprocal of $\frac{33}{7}$ is found by swapping the numerator and denominator.

Thus, the reciprocal of $\frac{33}{7}$ is \frac{7}{33}$.

Reciprocal of a Negative Fraction

If a fraction has a negative sign, its reciprocal also has a negative sign. In this case, simply take the reciprocal of the positive fraction and assign the negative sign to it. 

The reciprocal of a negative fraction $-\;\frac{a}{b}$ is written as $-\;\frac{b}{a}$.  (a, b are whole numbers numbers, $b  ≠  0$)

Example: The reciprocal of $\frac{-\;8}{11}$ is $\frac{-\;11}{8}$ or simply $-\;\frac{11}{8}$. 

Reciprocal of a Fraction with Exponents

The form of fractions with exponents is $\bigg(\frac{a}{b}\bigg)^{p}$, where p is any rational number; a and b are any whole numbers $\left(b  \neq 0\right)$, we must first use the laws of exponents to separate the numerator and denominator. 

An expression $\bigg(\frac{a}{b}\bigg)^{p}$ can be written as

$\bigg(\frac{a}{b}\bigg)^{p} = \frac{a^{p}}{b^{p}}$.

Now, swap the numerator and denominator to find the reciprocal. 

Therefore, the reciprocal of apbp is $\frac{b^{p}}{a^{p}}$.

Example: Find the reciprocal of $\bigg(\frac{2}{3}\bigg)^{3}$.

We can write $\bigg(\frac{2}{3}\bigg)^{3} = \frac{2^{3}}{3^{3}}$.

Hence, the reciprocal of $\bigg(\frac{2}{3}\bigg)^{3} = \frac{3^{3}}{2^{3}} = \bigg(\frac{3}{2}\bigg)^{3}$.

Facts about the Reciprocal of a Fraction

Conclusion

In this article, we learned about the reciprocal of a fraction, its definition, examples of reciprocal fractions, the reciprocal of mixed fractions, the reciprocal of fractions with exponents, the methods of finding reciprocal of fractions, and interesting facts. Let’s move ahead and solve a few examples and practice problems based on all these concepts.

Solved Examples on Reciprocal of a Fraction

1. Find the reciprocal of $\frac{5}{13}$.

Solution:

The reciprocal of a fraction is obtained by interchanging its numerator and denominator.

Hence, the reciprocal of $\frac{5}{13}$ is $\frac{13}{5}$.

2. What is the reciprocal of the sum of $\frac{5}{6}$ and $\frac{7}{15}$?

Solution: 

Sum of the given fraction $= \frac{5}{6} + \frac{7}{15} = \frac{25 + 14}{30} = \frac{39}{30} = \frac{13}{10}$

Hence, the reciprocal of sum $= \frac{10}{13}$.

3. If a is the reciprocal of $\frac{12}{13}$, then find the value of $a + 5$.

Solution: 

$a =$ Reciprocal of $\frac{12}{13} = \frac{13}{12}$

$a + 5 = \frac{13}{12} + 5 = \frac{13 + 60}{12} = \frac{73}{12}$

4. Find the reciprocal of $5\frac{2}{15}$.

Solution: 

To find the reciprocal of a mixed number, we first need to convert it to an improper fraction.

$5\frac{2}{15} = \frac{(15 × 5) + 2}{15} = \frac{77}{15}$

Reciprocal of $\frac{77}{15} = \frac{15}{77}$

Hence, the reciprocal of $5\frac{2}{15} = \frac{15}{77}$.

5. Find the reciprocal of $2\frac{4}{13}$?

Solution: 

We can write the given mixed fraction as an improper fraction.

$2\frac{4}{13} = \frac{(13 × 2) + 4}{13} = \frac{30}{13}$

Reciprocal of $2\frac{4}{13} = \frac{13}{30}$

6. John can mow a lawn in 5 hours. What is the reciprocal of the fraction representing John’s hourly mowing rate?

Solution: 

John can mow a lawn in 5 hours. 

John’s hourly mowing rate is $\frac{1}{5}$ of a lawn per hour because he can mow one lawn in 5 hours. 

Hence, the reciprocal of $\frac{1}{5}$ is $\frac{5}{1}$, or simply 5. 

Therefore, John’s reciprocal hourly mowing rate is 5 lawns per hour.

7. Find the reciprocal of $\bigg(\frac{5}{3}\bigg)^{-2}$?

Solution: 

 $\bigg(\frac{5}{3}\bigg)^{-2} = \bigg(\frac{3}{5}\bigg)^{2} = \bigg(\frac{9}{25}\bigg)$

Reciprocal of $\frac{9}{25} = \frac{25}{9}$

Practice Problems on the Reciprocal of a Fraction

Frequently Asked Questions about the Reciprocal of a Fraction