Repeating Decimals – Definition, Types, Examples, Facts, FAQs

What Are Repeating Decimals?

Repeating decimals are decimals in which a digit or a group of digits after the decimal point repeats indefinitely and at regular intervals such that the decimal representation becomes periodic. 

Repeating decimals are also known as “recurring decimals.”

Examples of repeating decimals: 0.3333…, 1.454545…, 0.626262…, etc.

Definition of Repeating Decimals

Repeating decimals or recurring decimals are the non-terminating decimals in which a digit or a group of digits are repeated at equal intervals after the decimal point.

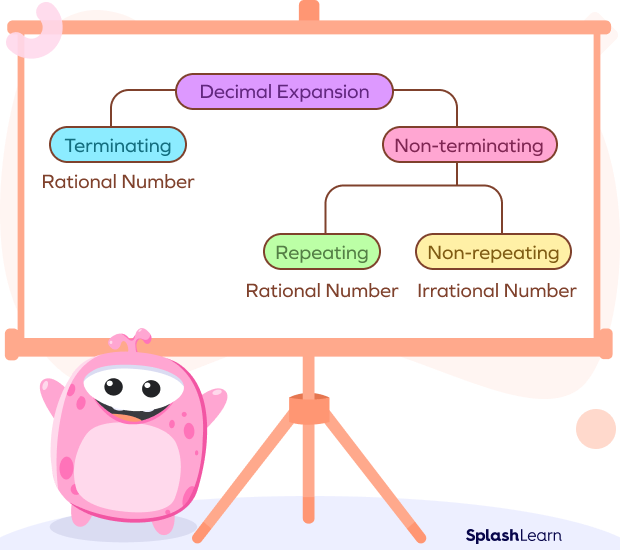
Types of Decimals

Decimals can be classified into two categories: terminating decimals and non-terminating decimals.

1. What are terminating decimals? 

Terminating decimals are decimals in which there are a finite number of digits after the decimal point. The digits after the decimal point terminate after a finite number of digits. 

2. What are non-terminating decimals? 

Non-terminating decimals are the decimals in which there are an infinite number of digits after the decimal point.

The non-terminating decimals are further classified as

a) Repeating decimals: Digits or a group of digits repeat themselves

b) Non-repeating decimals: Digits do not follow any repeating pattern

Representation of Recurring Decimals

We generally write repeating decimals using an ellipsis (a set of dots, i.e., “…”). To express that a digit or a group of digits is repeating, we can also write a dot or a bar on the top of the recurring part. 

Repeating Decimal	Notation
0.555…(5 repeats forever.)	0.5
1.2525…(The digits “25” repeat forever.)	1.25
5.987987987…(The digits “987” repeat forever.)	5.987
0.999…(9 repeats forever.)	0.9

Period of a Repeating Decimal Number

The recurring part (the recurring digit or the group of recurring digits) in a non-terminating and repeating decimal is called the period of the decimal.

Example: What is the period of the decimal expansion of $\frac{1}{7}$?

$\frac{1}{7} = 0.\overline{142857}$

Period $= 142857$

Periodicity of a Repeating Decimal

The number of digits that repeat in a recurring decimal is called the periodicity (or the length of the period) of the repeating decimal.

Example: The periodicity of $0.\overline{142857}$ is 6.

Repeating decimal	Period (Which digits are repeating?)	Periodicity (How many digits are repeating?)
1.2	2	1
0.132	132	3
586.45	45	2

Repeating Decimals as Rational Numbers

All repeating decimals are rational numbers. All rational numbers can be written in the decimal form that has the same mathematical value, with the help of the long division method. 

The decimal expansion of a rational number can be of two types only:

1. Terminating decimal expansion
2. Non-terminating but repeating decimal expansion

Rational Numbers with Repeating Decimal Expansion

We divide the numerator of the rational number by its denominator using the long division method to find the decimal expansion. The quotient obtained represents the decimal representation of that rational number. 

Let’s consider an example.

Example: What is the decimal expansion of the rational number $\frac{4}{9}$?

Divide 4 by 9.

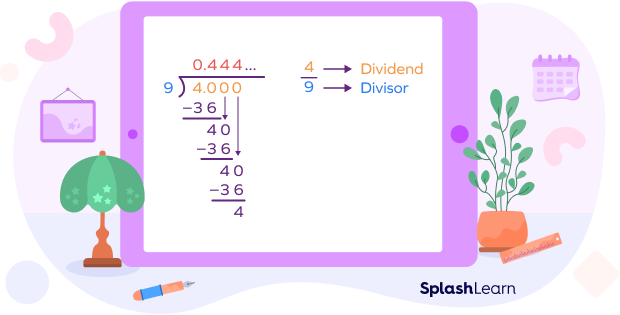
$\frac{4}{9} = 0.444..=0.\overline{4}$

Thus, the rational number $\frac{4}{9}$ has a non-terminating and repeating decimal expansion. 

How to Convert Recurring Decimals to Fractions

Repeating or recurring decimals have a repetitive pattern of digits after the decimal point. Let’s understand the steps to convert a repeating decimal as a fraction.

Step 1: Identify the repeating digits in the given decimal number. 

Step 2: Equate the decimal number to any variable. Make sure that only repeating digits come after the decimal point. 

Step 3: Multiply both sides of the equation by a power of ten equal to the number of repeating digits. 

Step 4: Subtract the equation obtained in step 3 from the equation obtained in step 2. 

Step 5: Simplify to get the answer. 

Example 1: Write 0.3333… as a fraction.

Let $x = 0.3333$… …(i)

Repeating digit $= 3$

Number of repeating digits $= 1$

$10x = 3.3333$… …(ii)

Subtracting (ii) from (i), we get 

$10x\;-\;x = 3.333…\;-\;0.3333…$

$9x = 3$

$x = \frac{3}{9}$

$x = \frac{1}{3}$

Example 2: Convert 0.5232323… into a fraction.

The repeating digits in the given decimal number are 23. 

Let $x = 0.5232323$….(i)

Notice that we need to shift the non-repeating digit 5 to the left of the decimal point. Multiply (i) by 10.

$10x = 5.232323$….(ii)

There are two repeating digits, so we multiply the above equation by 100. We will get,

$1000x = 523.232323$…(iii)

Subtract (ii) from (iii).

$990x = 518$

$x = \frac{518}{990}$

$x = \frac{259}{495}$

Example 3: Convert 7.324242.. into a fraction.

Let $x = 7.3242424$…

Let’s keep only repeating digits after the decimal point.

$10x = 73.2424$… …(i)

Multiply both the sides by the power of 10 equal to the number of repeating digits. Thus, we multiply by $10^2 = 100$.

$1000x = 7324.2424$… …(ii)

Subtracting (ii) from (i), we get

$1000x \;-\; 10x = 7324.2424…\;-\;73.2424$..

$\Rightarrow 990x = 7251$

$\Rightarrow x = \frac{7251}{990}$

$\Rightarrow x = \frac{2417}{330}$

Properties of Repeating Decimals

• All repeating decimals are rational numbers. They can be expressed in the form of $\frac{p}{q}$, where $q \neq 0,\; p$ and q are integers. 

• A real number is rational if and only if its decimal expansion is repeating or terminating. 

• Repeating decimals have an infinite number of digits.

• Repeating decimals are non-terminating decimals that show a certain repetitive pattern of digits after the decimal point. 

• If a digit or a group of digits after the decimal point in a non-terminating decimal are not repeating, the decimal expansion represents an irrational number.

Solved Examples on Repeating Decimals

1. Convert the repeating decimal 1.8888… into a fraction.

Solution: 

Let $x = 1.8888$… — (1)

Multiplying both the sides by 10, we get

$10x = 18.8888$… — (2)

Subtracting (1) from (2), we get

$10x \;-\; x = 18.888$…$-1.888$…

$9x = \frac{1}{7}$

$x = \frac{17}{9}$

2. What fraction is equivalent to the repeating decimal number 0.434343…?

Solution: 

Let $x = 0.434343$… — (1)

Multiplying both the sides by 100, we get

$100x = 43.434343$…. — (2)

Subtracting (1) from (2), we get

$100x \;-\; x = 43.434343…\;-\;0.434343….$

$99x = 43$

$x = \frac{43}{99}$

3. Convert 0.567567567… into a fraction.

Solution: 

Let $x = 0.567567567$… — (1)

Multiplying both the sides by 1000

$1000x = 567.567567$… — (2)

Subtracting (1) from (2), we get

$1000x\;-\;x = 567.567567567$…$-0.567567567$…

$999x = 567$

$x= \frac{567}{999} = \frac{189}{333} = \frac{63}{111} = \frac{21}{37}$

4. Which fraction is equivalent to 2.34444…?

Solution: 

Let $x = 2.34444$… 

Multiplying both the sides by 10

$10x = 23.4444$… — (1)

Multiplying both sides by 10 

$100x = 234.4444$… — (2)

Subtracting (1) from (2), we get

$100x\;-\;10x = 234.444$…$-23.444$…

$90x = 211$

$x = \frac{211}{90}$

5. What fraction is equivalent to the repeating decimal number 24.579579…? 

Solution: 

Let $x = 24.579579$… — (1)

Multiplying both the sides by 1000

$1000x = 24579.579579$… — (2)

Subtracting (1) from (2), we get

$1000x\;-\;x = 24579.579579$…$-24.579579$…

$999x = 24,555$

$x = \frac{24555}{999} = \frac{8185}{333}$

Practice Problems on Repeating Decimals

Frequently Asked Questions on Repeating Decimals