What Are Significant Figures?
Significant figures (or significant digits) are the number of digits in a given value or a measurement, necessary to decide the accuracy and precision of measurement.
They are important in scientific or technical measurements.
“Significant” means important. They refer to the reliable digits in the given number, which are sufficient to convey accurate information. They also help us round off measurement values or the outcome of a calculation.
Significant Figures Definition
Significant figures (or significant digits) are the number of digits important to determine the accuracy and precision of measurement, such as length, mass, or volume.
Significant digits in math convey the value of a number with accuracy. They are considered substantial figures that contribute to the precision of a number.

What Are the Rules for Significant Figures?
Certain rules help us determine the number of significant figures. These rules are as follows:
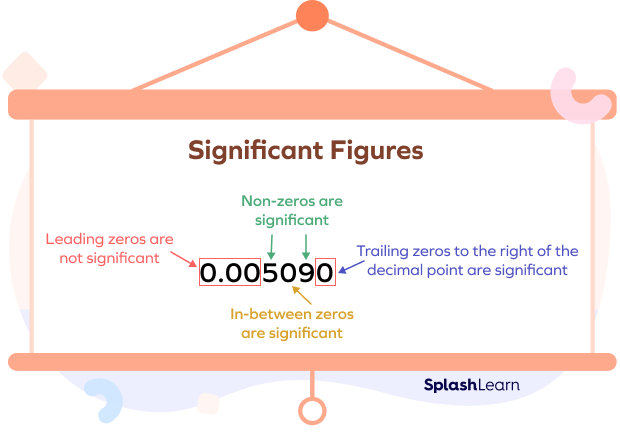
(1) All non-zero digits are significant.
How many significant figures in 20? Two!
652.1 miles $- 4$ significant figures.
3.4 inches $- 2$ significant figures.
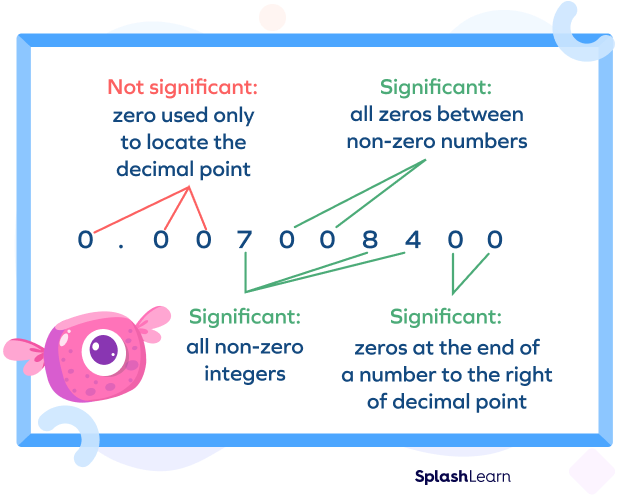
(2) All zeros in between non-zero digits are significant.
23.0041 $- 6$ significant digits.
4005 feet $- 4$ significant digits.
(3) Zeros on the right of a decimal point and before (or to the left of) the first non-zero digit are not significant. They only represent the position of the decimal point.
$0.003$ $-$ $1$ significant digit.
$0.0034$ $-$ $2$ significant digits
(4) Zeros on the right of a decimal point are significant, provided there is no non-zero digit after them.
$7.00$ $-$ $3$ significant digits.
(5) Zeros on the right of the last non-zero digit after a decimal point are significant. So, final zeros or trailing zeros in the decimal part are significant.
$0.6500$ $-$ $4$ significant digits
$12.300$ $-$ $5$ significant digits
(6) In a measurement value, zeros that occur on the right of the last non-zero digit are significant.
2650 inches $- 4$ significant digits
Let’s take a look at a few examples for better understanding.
Significant figures examples:
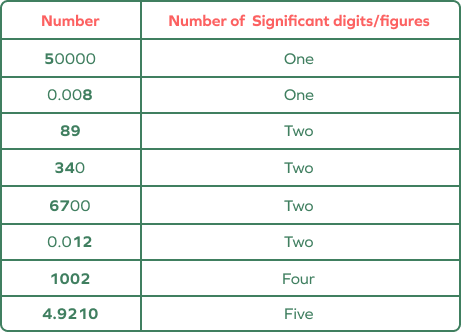
In summary:
How to Round Off Significant Figures
To round off significant figures, we have to omit one or more digits from the right side of the number until we reach the number of significant digits that we want to round it off to.
First, we have to look at the digit on the right end of the number (to the right of the digit we want to round it off to).
- If the digit is lower than 5, the number is rounded off to the lower number.
- If the digit is greater than or equal to 5, the number is rounded up to the higher number.
If there is more than one digit on the left, the number will be rounded off as a whole and not digit by digit.
Confused? Let’s look at an example!
Example: How many significant figures are there in 0.04582? Four! The four significant digits are 4, 5, 8, and 2.
Let’s round off this number to three significant digits.
Check the last digit, which is 2.
We will round it to 0.0458 since the last digit, 2, is less than 5.
If we want to round it off further to 2 significant digits, then it will be rounded up to 0.046 because the last digit, 8, is greater than 5.
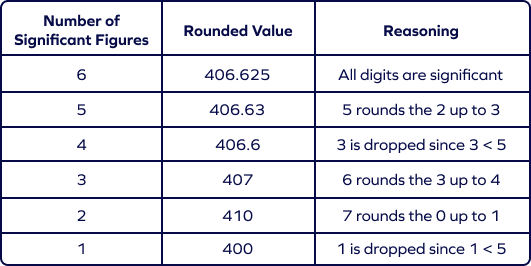
Here’s an example of a decimal rounded from 6 significant digits to 1 significant digit:
Multiplication and Division with Significant Figures
When multiplying and dividing significant figures, we follow the given steps.
- Identify significant digits of each number.
- Find the least number of significant digits in any of the numbers.
- Multiply or divide the numbers in the problem as you would normally.
- Once you get the product or quotient, round off the number so it does not have more significant digits than the number with the least significant digits.
The LEAST number of significant figures in the given numbers determines the number of significant figures in the answer.
Example: $1.4 \times 2 = 2.8$
1.4: 2 significant digits and 2: 1 significant digit
Least number of significant digits $= 1$
So, we round 2.6 to 3 since the last digit $6 \gt 5$.
Addition and Subtraction with Significant Figures
- For each number, check the number of significant figures to the right of the decimal point (in the decimal part).
- Identify the LEAST number of significant digits.
- Add or subtract the numbers in the usual manner.
- When you get the final sum or difference, round off the number so that it does not have more significant digits on the right of the decimal point than the least number you found earlier.
Example: Add 3.240 inches and 8.12 inches.
Here, 3.240: 3 significant figures in the decimal part
8.12: 2 significant figures in the decimal part
Adding two decimals, we get
$3.240 + 8.12 = 11.360$, which has 3 significant digits in the decimal part.
So, we round it off to two significant figures to get 11.36.
Fun Facts!
Here are some fun facts about significant figures:
- Significant digits are also called “sig figs.”
- In earlier times, significant digits were used to refer to the non-zero digits on the left of the zeros on the right end of a number. For example, 4500 would have two significant digits.
- In modern times, significant digits are used for measurements and accuracy. Rounding errors would often affect the accuracy of mathematical and scientific calculations. For this reason, there was a need to develop rules for rounding off numbers and measurements.
Conclusion
Once you’ve learned the rules, you can easily count the significant figures in a number. The rules for zeros, decimal points, and rounding off are the most important. Keep practicing, and you’ll be able to add, subtract, divide and multiply without a sweat!
Solved Examples
1. How many significant digits are there in the number 0.002?
Solution: There is one significant figure in 0.002. Leading zeros are not significant.
2. How many significant digits are there in the number 67.30?
Solution: There are four significant figures in 67.30. Final or trailing zeros are significant.
3. Add these numbers by applying the significant figures rules: 42, 7.8, 6.50, 12.
Solution: $42 + 7.8 + 6.50 + 12 = 68.3$
For the given numbers, the least number of significant digits on the right of the decimal point is 1. So, the sum 68.3 will stay as 68.3 since it has one significant number after the decimal point.
4. Round off the number 43.8 to two significant digits.
Solution: Looking at the last digit, 8, we can see it is more than 5.
Given that the number has to be rounded off to two significant digits, it will be rounded off to 44.
5. Multiply the numbers 11.6, 8.30, and 22.001.
Solution: Out of the given numbers, the least number of significant numbers is 3. Multiplying the numbers: $11.6 \times 8.30 \times 22.001 = 2118.25268$
To round it off to 3 significant numbers, we have to look at the number right of 3 significant numbers, which is 8.
Since it is greater than 5, the number will be rounded off to 212.
Practice Problems
Significant Figures
Determine the number of significant figures in the number 23.02.
There are four significant digits in this number. Remember, zeros after a decimal point and before a significant number are not significant.
Round off the number 53.46 to three significant digits.
The last digit is greater than 5, so we round off the number to 53.5.
Subtract these numbers and round off the difference, applying the rules for significant numbers: 50.60 and 20.3.
$50.60$ $–$ $20.3 = 30.3$. Out of the given numbers, the least number of significant digits after the decimal point is 1. So, the difference will remain at 30.3.
Divide the numbers 13.7 and 3.2, applying the rules for significant numbers.
Dividing the numbers we get: $\frac{13.7}{3.2} = 4.28125$
In the given numbers, the least number of significant numbers is 2.
So, 4.28 has to be rounded off down to 2 significant numbers, which will make it 4.3.
How many significant figures are there in 9.000?
There are 4 significant digits in the number 9.000. Zeros after a decimal point are significant if there is no non-zero number after them.
Frequently Asked Questions
Why are significant digits important?
The more significant digits a number has, the higher degree of precision it carries. For example, 36.65 gives us a more precise indication than 36.
How do you round off significant digits when the digit on the right is exactly 5?
When the digit is exactly 5, the number is rounded either up or down.
Can a number without a decimal point have significant digits?
Yes, in a whole number like 1465, all the digits are significant.
Is a non-zero digit always significant, even if it is after the decimal point?
Yes, a non-zero digit is always significant, even if it is after the decimal point.
How are significant digits helpful in real life?
Significant figures are helpful in real life because they allow for more accurate results in calculations, especially in sciences, applied mathematics, or technical fields. The final number after calculations can represent the measurement more closely.
What is an ”exact number”?
The numbers that have no uncertainty are called exact numbers. They have defined values. Example: Exactly 12 inches make one foot.
















