What Are Skew Lines in Geometry?
Skew lines in geometry are non-coplanar lines that are neither parallel nor intersecting. Skew lines can exist only in three-dimensional or higher-dimensional space.
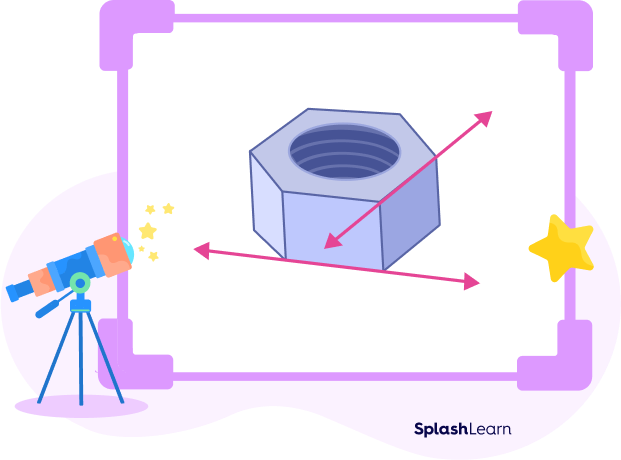
- What are parallel lines and intersecting lines?
Parallel lines are a pair of straight lines that are in the same plane and never intersect, no matter how far they are extended. Intersecting lines are lines that cross each other at a specific point and lie in the same plane then they are known as intersecting lines.
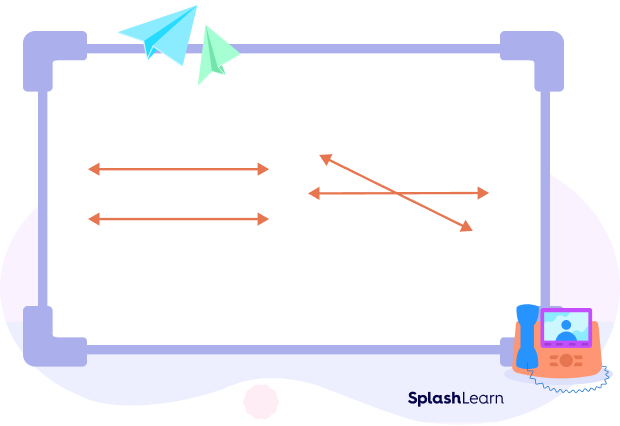
- What are coplanar lines?
Coplanar lines are lines that lie in the same plane.
Recommended Games
Skew Lines: Definition
Skew lines are a pair of non-coplanar lines that do not intersect and are not parallel.
Skew lines are lines that are
- non-coplanar
- non-parallel
- non-intersecting
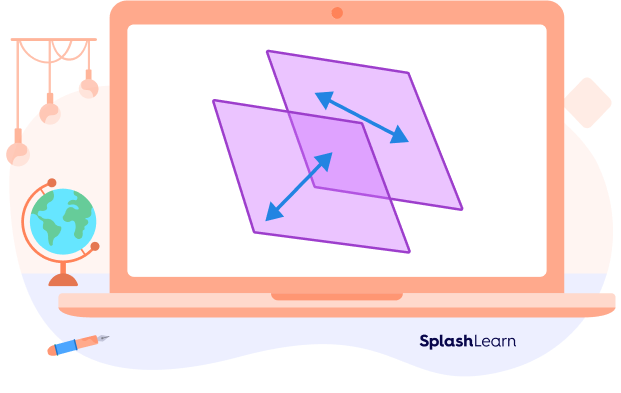
Properties of Skew Lines
- They are not parallel.
- They do not intersect.
- They lie on different planes (non coplanar).
- Skew lines cannot exist in a 2D plane.
- Skew lines can only exist in 3 dimensions or higher.
Real-life Examples of Skew Lines
- Take a look at two lines drawn on the overpasses shown below. They never cross each other and are not parallel to each other. Also, they do not lie on the same plane. These lines represent skew lines.

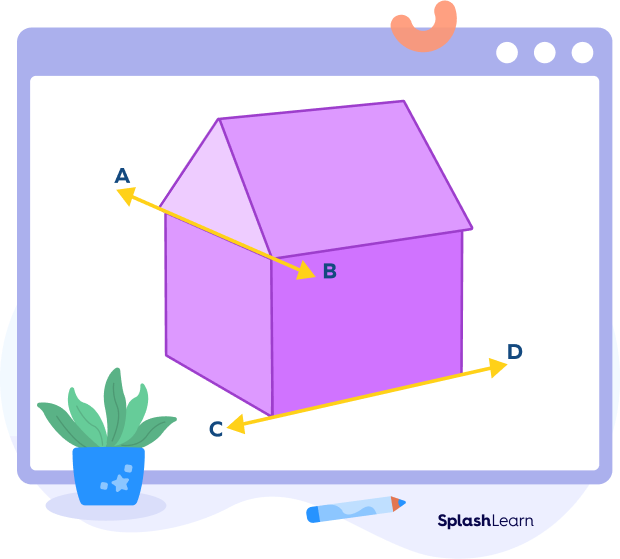
- You can observe that the baseline CD of the house and the line AB on the top are neither parallel nor intersecting. Also, they lie in different planes. They represent skew lines.
- Similarly, the lines shown on a signboard are neither parallel nor intersecting. They lie in different planes.

Skew Lines vs. Parallel Lines
The two kinds of lines that never cross each other are skew lines and parallel lines. While two skew lines can never be on the same plane, two parallel lines can exist on a plane.
| Skew Lines | Parallel Lines |
|---|---|
| Skew lines cannot be on the same plane. They are not coplanar. | Parallel lines lie on the same plane. They are always coplanar. |
 |  |
How to Find Skew Lines
To find a pair of skew lines on solids, we can follow the following steps.
Step 1: Select any line. Say a line on the floor of your room.
Step 2: Choose another line such that it does not share a plane with the first line, and is not parallel to the first line. You can choose a line drawn on the wall of your room.
In other words, we can say that the lines should be:
i) non-intersecting ii) non-parallel, and iii) non-coplanar.
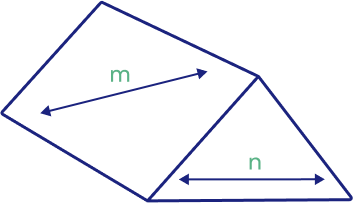
Example:

In the above figure, lines m and n lie on two different faces of a cuboid. Thus, they are not coplanar.They are not parallel. They do not intersect with each other.
Lines m and n are non-intersecting, non-parallel, and non-coplanar.
Hence, they are skew lines.
Skew Lines in 3D Objects
We can identify skew lines on edges or lines on the faces of three-dimensional geometric shapes.
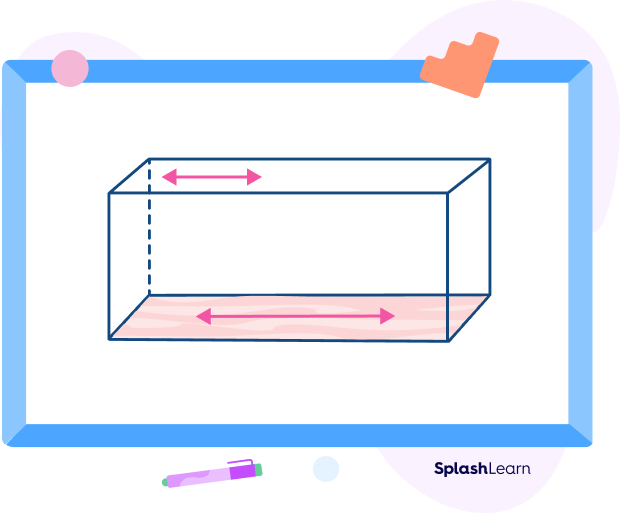
In the given figure, the line drawn on the base and the line on the top face are pairs of skew lines as they are not parallel; they do not intersect; and they do not lie on the same plane.
Similarly, check out skew lines on a square box or a cube.
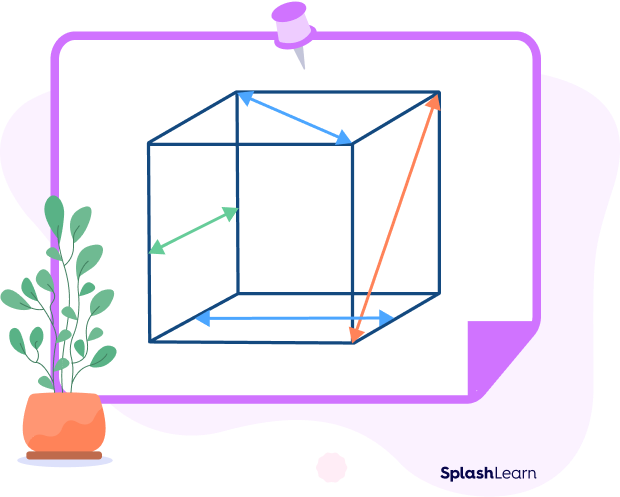
Skew Lines on a Cube
It is simple to find skew lines in three-dimensional figures such as cubes, cuboids, etc. Let’s identify the skew lines on a cube.
To find a pair of skew lines in a cube follow the given steps.
- Step 1: Identify a pair of lines that do not intersect one another.
- Step 2: Check if these pairs of lines are also non-parallel to each other.
- Step 3: Check if these pairs of non-intersecting and non-parallel lines are also non-coplanar to each other.
Facts about Skew Lines
- Two straight lines in the same plane must either intersect or parallel to each other.
- The skew lines exist only in three-dimensional or higher-dimensional space.
- Skew lines are neither parallel nor intersecting, further it does not lie in the same plane.
Conclusion
Skew lines are the lines that are non-coplanar, non-intersecting, and non-parallel. We discussed properties, how to identify skew lines on 3D shapes with real life examples.
Let’s solve a few examples for better comprehension.
Solved Examples on Skew Lines
- Which of the following shapes may have skew lines?
- Rectangle
- Hexagons
- Octagon
- Cuboids
- Cube
Solution:
The skew lines exist only in three-dimensional or higher-dimensional space.
Rectangle, hexagon, octagon are polygons, which are 2D geometric shapes.
In the given list of shapes, only cuboid and cube are three-dimensional shapes.
Hence, skew lines can be found on them.
- In the figure given below, identify two pairs of skew lines.
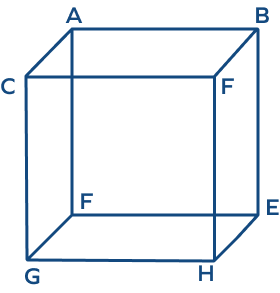
Solution:
In the given figure, there are many skew lines possible.
The edges AB, DH are skew.
Also, the edges CD, EH are non-intersecting and non-parallel. Also, they do not lie in the same plane.
Hence, we can write any two pairs of skew lines as:
AB, DH
CD, EH
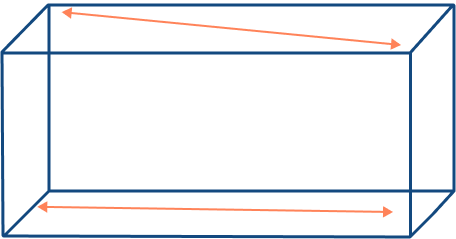
- Draw a pair of skew lines in a cuboid.
Solution:
A pair of skew lines are drawn on a cuboid, one at the bottom face and another at the top face of the cuboid.
Practice Problems on Skew Lines
Skew Lines - Definition, Facts, Examples, FAQs, Practice Problems
Skew lines are
The skew lines are a pair of lines that are non-parallel, non-intersecting, and non-coplanar.
Which of the following lines are equidistant?
Parallel lines are lines in the same plane that are equidistant from each other and never meet.
Skew lines are defined as lines in space that are
Skew lines are defined as lines in space that are non-parallel, non-intersecting, and non-coplanar.
Which of the following figures have edges that may represent skew lines?
The skew lines exist only in three-dimensional or higher-dimensional space. Hence out of the given options skew lines are possible only on the cube.
The minute hand and hour hand of a clock form _______ lines.
The two hands of a clock, the minute hand and hour hand are connected in the center of a clock. This indicates that they are forming intersecting lines.
Frequently Asked Questions about Skew Lines
Are skew lines parallel to each other?
No, skew lines are not parallel to each other.
Is there any similarity between skew lines and parallel lines?
Both parallel and skew lines never cross each other. However, skew lines lie in different planes and parallel lines lie in the same plane.
How many skew lines are there in a cube?
Since a cube is a three-dimensional figure, hence a cube can have multiple skew lines. As long as they do not intersect, are not parallel to one another, and are non-coplanar, skew lines in a cube can be found on any two faces.
How to find skew lines in any 3D figure?
To find skew lines in any 3D figure follow the following steps
Step 1: Identify pairs of lines that do not intersect one another.
Step 2: Check if these pairs of lines are also non-parallel to each other.
Step 3: Check if these pairs of non-intersecting and non-parallel lines are also non-coplanar to each other.
Can skew lines intersect?
No, skew lines never intersect.


























