What Is a 60-Degree angle?
A 60-degree angle is an angle that represents one-sixth of a complete angle (a circle). It is an acute angle since the angle measure is less than 90 degrees (a right angle). A 60-degree angle is expressed as $\frac{\pi}{3}$ in radians.
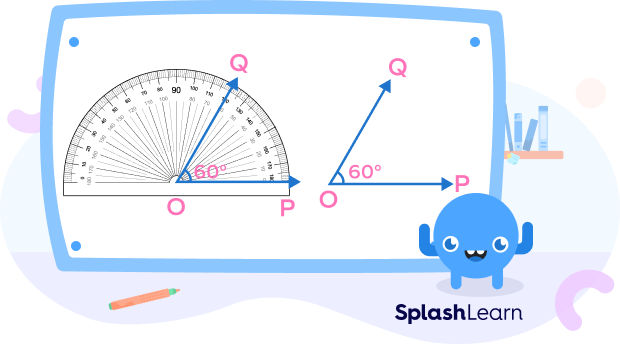
What does a 60-degree angle look like? Let’s see!
- What is an angle?
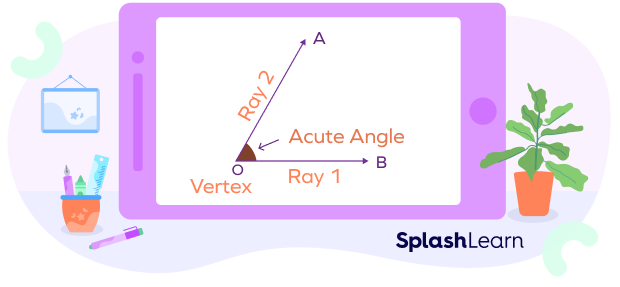
Angle is a geometric figure formed by two rays sharing a common endpoint called vertex. The two rays are called the arms or sides of the angle.
An angle is measured in degrees (represented by symbol °) or radians (abbreviated as rad). There are various types of angles like acute angle, obtuse angle, right angle, etc., based on the angle measure.
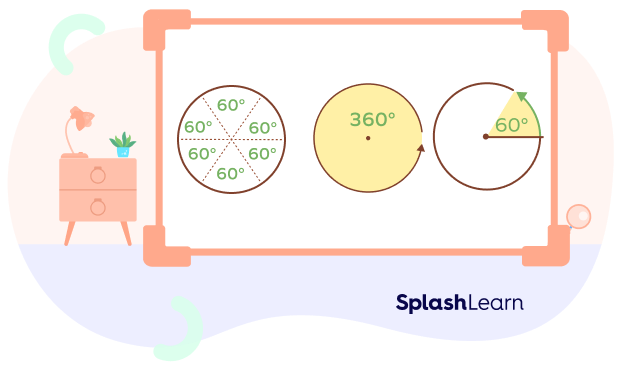
If we divide a circle in 6 equal parts, the angle made at the center by each sector is 60o. Thus, it represents one-sixth of 360o angle, a complete circle. Take a look at the given diagram to observe a 60-degree angle in a circle.
Recommended Games
Meaning of 60-Degree angle
When two rays come together at a vertex, they create an angle. When we rotate the initial ray by 60 degrees, it results in the formation of a 60-degree angle. This angle measures the amount of rotation or deviation from the initial direction.
Recommended Worksheets
How to Construct a 60-Degree Angle
Constructing an angle is the most basic and important skill in geometry. The 60-degree angle can very easily be constructed by using a protractor. It is also the easiest angle to draw using a ruler and compass (without using a protractor).
- How to Construct a 60-degree angle Using a Protractor
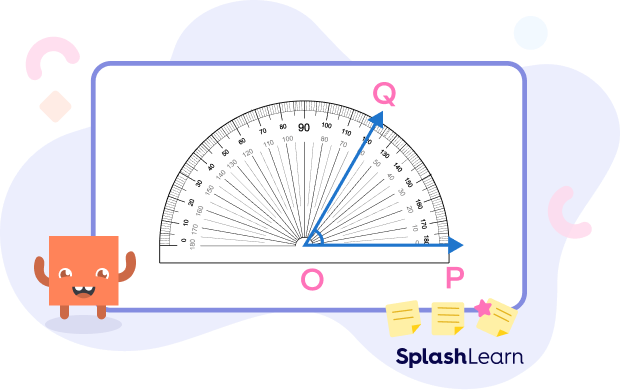
Let us construct a 60-degree angle with the help of a protractor.
Step 1: Draw a line segment OP of a suitable length. Align the center of the protractor with the point O such that the baseline of the protractor aligns with the line segment OP.
Step 2: Look for 60 degrees reading on the inner scale. Mark a dot and name it Q.
Step 3: Join O and Q.
Thus, m∠POQ = 60o
- How to Construct a 60-Degree Angle Using a Ruler and Compass
Let us construct a 60-degree angle with the help of a ruler and a compass.
Step 1: Using a ruler draw a line segment QR of any convenient length.
Step 2: Take the compass and open it up to a convenient radius. Place its pointer at Q and with the pencil-head make an arc which meets the line QR at say, Y.
Step 3: Keeping the width unchanged, place the tip of the compass on the point Y and draw another arc which passes through P and cut the arc drawn in the previous step at some point (say X).
Step 4: Connect the points Q and X with a straight line and extend it to form a ray QP.
Hence, the required ∠PQR = ∠XQY = 60o.
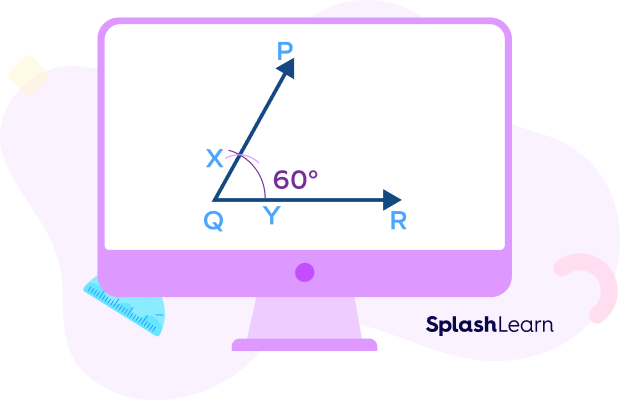
Equilateral Triangle: 60-Degree Angle Triangle
All sides of an equilateral triangle are equal and angles are congruent. The measure of each angle of an equilateral triangle is 60°. Therefore, it is also called a “60-degree angle triangle.
60-Degree Angles Around Us
There are many real-life examples of a 60-degree angle.
- When the analog clock reads 02:00, the angle formed between the minute hand and the hour hand is also a 60-degree angle.
- If a round cake or a pizza is cut in 6 equal pieces, then 1 piece represents a 60-degree angle at the center.

Facts about a 60-Degree Angle
- In geometry, an angle that measures 60 degrees is an acute angle.
- The angle of 30 degrees can be constructed by bisecting the angle of 60 degrees.
- In an equilateral triangle, all the angles of the triangle are equal to 60 degrees.
- A negative 60-degree angle is the angle of 60 degrees measured in the counterclockwise direction, below the x-axis.
Conclusion
In this article, we learned about a 60-degree angle, the definition and meaning, and its construction using a protractor and a compass. We also discussed some real-life examples of this acute angle. Let’s solve some examples and practice MCQs for better understanding.
Solved Examples on a 60-Degree Angle
Example 1: What is the measurement of one-third of a 180o angle?
Solution:
One-third of 180o angle $= \frac{180^{\circ}}{3} = 60^{\circ}$
One-third of a 180o angle is a 60o angle.
Example 2: How many 60-degree angles make a complete angle?
Solution:
Observe the given image. An angle of 60 degrees is an angle that represents one-sixth of a complete angle. Complete angle is a 360-degree angle. So, a total of six 60-degree angles are present in one complete angle.
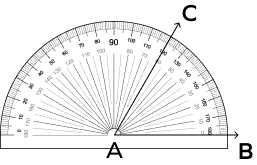
Example 3: Construct an angle of 60 degrees using a protractor.
Solution:
- Draw a line segment of any measure. Now, place the center of the protractor on point A such that the line segment AB is aligned with the baseline of the protractor.
- Now, look for the 60° marking in the inner scale of the protractor and mark a point C with a dot. Join A and C.
- m∠CAB = 60o
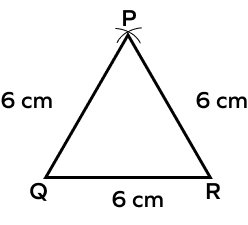
Example 4: Construct an equilateral triangle without constructing a 60-degree angle.
Solution:
An equilateral triangle has all sides congruent and all angles are 60o. Let’s construct an equilateral triangle with each side 6 cm in length.
1) Draw a line segment QR with length 6 cm.
2) Taking 6 cm as radius and Q as a center, draw an arc with the help of a compass.
3) Taking 6 cm as radius and R as a center, draw another arc that intersects the previous arc at the point P.
4) Join PQ and PR.
△PQR is an equilateral triangle.
Practice Problems on a 60-Degree Angle
60-Degree Angle - Meaning, Construction, Examples, Facts, FAQs
A 60-degree angle is an _____angle.
A 60-degree angle is an acute angle, which means it is less than 90 degrees.
An acute-angled triangle has one 60-degree angle. What is the sum of the measures of the other two angles?
The sum of all angles in a triangle $= 180^{\circ}$
The sum of the measures of the other two angles $= 180^{\circ} \;-\; 60^{\circ} = 120^{\circ}$
The time on an analog clock when the hour and minute hand make a 60-degree angle is ________.
Complete angle of clock is of $360^{\circ}$. Each division on a clock represents a $30^{\circ}$ angle.
Thus, when it is 10 am, the hour and minute hand are separated by two divisions.
Angle $= 30^{\circ} + 30^{\circ} = 60^{\circ}$

Measure of an acute angle is ________ the measure of a right angle.
Acute angle is an angle which is less than a right angle (90 degree angle).
Which of the following is NOT an acute angle?
Acute angles are the angles less than 90 degrees.60,45 and 30 degrees are the angles less than 90 degrees, while 90 degree is a right angle.
Frequently Asked Questions about a 60-Degree Angle
Why is a 60-degree angle expressed as $\frac{pi}{3}$ in radians?
As we know from the formula of radians to degrees,
Angle in Degrees = Angle in Radians $\times \frac{180^{\circ}}{\pi}$
$\frac{\pi}{3}$ in Degrees $= \frac{\pi}{3} \times 180^{\circ}$
$\frac{\pi}{3}$ in Degrees $= \frac{180^{\circ}}{3}$
$\frac{\pi}{3}$ in Degrees $= 60^{\circ}$
Can a triangle have only one acute angle?
A triangle can never have only one acute angle. If a triangle has 1 acute angle, the other angles will either be right angles or obtuse angles which is not possible as the sum of interior angles of a triangle is always 180°. So, every triangle needs to have at least 2 acute angles.
What is meant by angle in standard position?
An angle is in standard position if its vertex is located at the origin, and its initial side extends along the positive x-axis. Look at the image given below
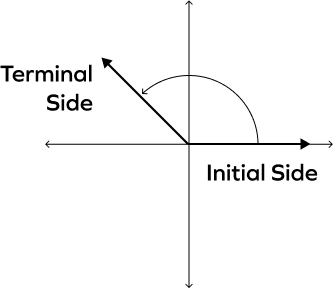
- When an angle is measured counterclockwise from the initial side to the terminal side, it is considered a positive angle.
- Conversely, if an angle is measured in a clockwise direction, it is classified as a negative angle.
- An angle in standard position between 0 degrees and 90 degrees is situated in Quadrant I, where all coordinates are positive.
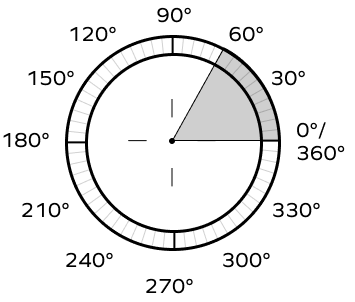
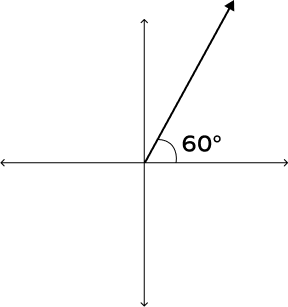
What does a 60 degrees angle in standard position look like?
An angle is said to be in the standard position if its vertex is located at the origin, and its initial side extends along the positive x-axis. In the picture given below, we can see what a 60-degree angle in a standard position looks like.
Is 60 degrees a right angle?
No, an angle that measures 90 degrees is called right angle. A 60-degree angle is an acute angle.






























