Circle Theorems: Definition, Formulas, Steps, Examples, FAQs

What Are Circle Theorems in Geometry?

The circle theorems in geometry are statements that prove significant results about circles. These theorems provide important information or facts about various parts of a circle. 

We can use circle theorems and previous knowledge of properties of a circle to calculate missing angles. The circle angle theorems give us the rules for finding the measurements of angles in a circle.

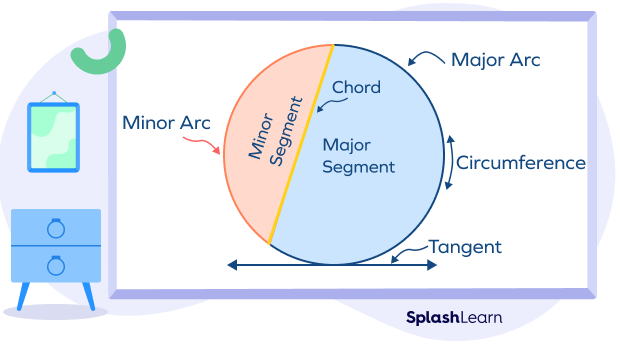
A circle is a locus of points that are equidistant from a fixed point called center. Different theorems are based on the various parts of a circle, such as radius, central angles, tangents, sectors, the chords, etc. These theorems help us to solve many problems in geometry easily.

Before we discuss the theorems, let’s revise the parts of the circle using a diagram.

Important Terms Related to Circle Theorems

Here are a few important terms that are commonly used in the statements of circle theorems.

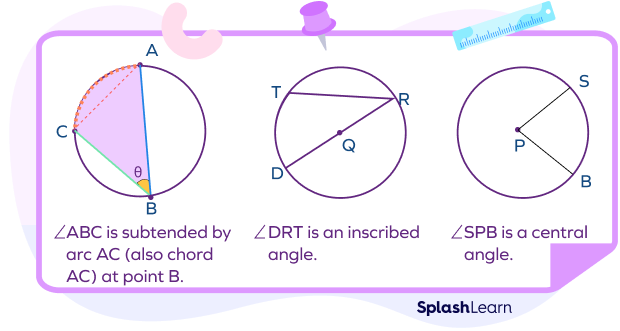
Subtended angle: The angle made by something (arc, chord, etc) from a given viewpoint. An angle within a circle created by two chords meeting at a point on the circumference. In a circle, there are various angles that can be formed joining the endpoints of arcs and those angles are termed subtended angles.

Inscribed Angle: An angle made from points lying on the circle’s circumference. It can also be defined as the angle subtended at a point on the circle by two given points on the circle. Thus, it is formed by two chords that have a common endpoint on the circle. 

Central Angle: An angle whose vertex is the center O of a circle and whose legs (sides) are radii intersecting the circle in two distinct points.

Circle Theorems

We will discuss the following circle theorems in detail.

1. Alternate segment theorem
2. The angle at the center theorem
3. Angles in the same segment theorem
4. Angle in a semicircle theorem
5. Chord of a circle theorem
6. Cyclic quadrilateral theorem
7. Tangent of a circle theorem-1
8. Tangent of a circle theorem-2

Circle Theorem 1: Alternate Segment Theorem

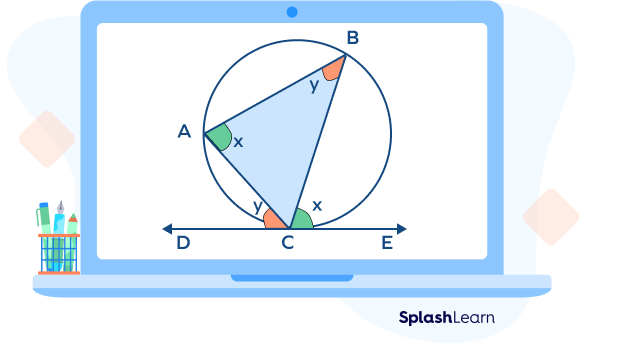
Here, according to the alternate segment theorem, 

• ∠x = ∠BCE = ∠BAC

Here, ∠BCE is the angle made by the tangent and the chord BC at the point of contact.

∠BAC is the angle made by the same chord BC in the alternate segment BAC.

• Similarly, ∠y = ∠ABC = ∠ACD

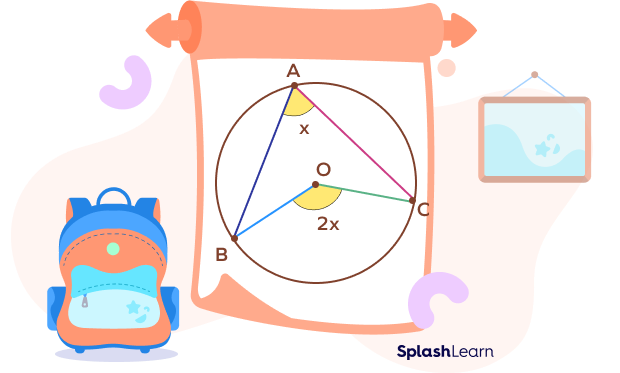
Circle Theorem 2: Central Angle Theorem (The Angle at the Center Theorem)

Here, the angle BAC is known as the inscribed angle, an angle made from points lying on the circle’s circumference.

The angle BOC is the central angle, an angle whose vertex is the center O of a circle and whose legs (sides) are radii intersecting the circle in two distinct points B and C.

Thus, the theorem states that an inscribed angle ∠BAC = x° is half of the measure of the central angle ∠BOC = 2x°.

∠BOC = 2 ∠BAC.

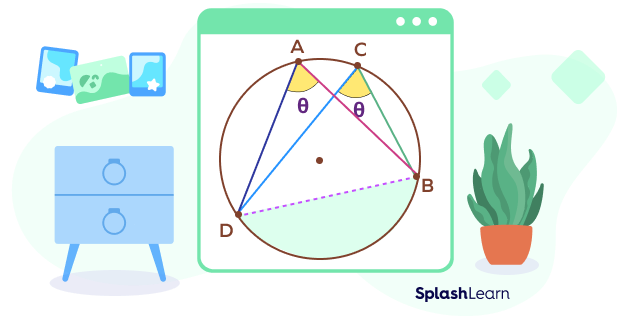
Circle Theorem 3: Angles in the Same Segment Theorem

Here, according to the angles in the same segment theorem: ∠BAD = ∠BCD

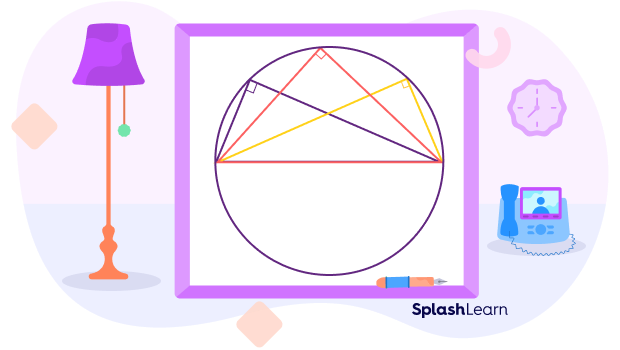
Circle Theorem 4: Angle in a Semicircle Theorem

In other words, an angle subtended by a circle’s diameter is always a right angle.

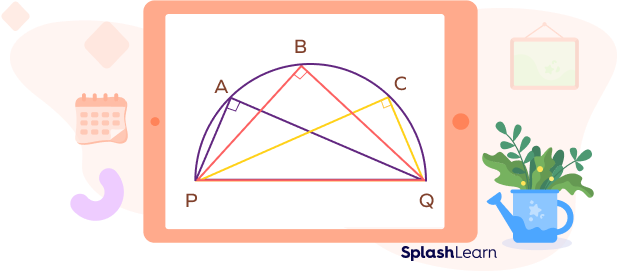
Here, according to the angle in a semicircle theorem: ∠A = ∠B = ∠C = 90⁰

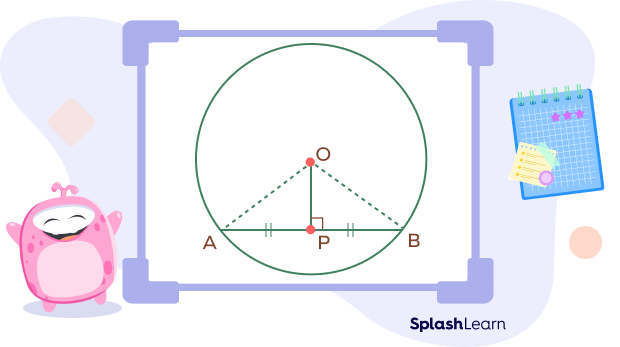
Circle Theorem 5: Chord of a Circle Theorem

Here, according to the chord of a circle theorem, we have 

∠OPA = ∠OPB = 90⁰

AP = PB

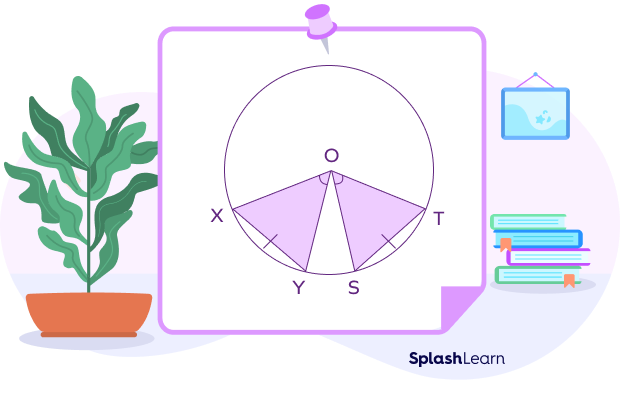
Circle Theorem 6: Angles Subtended by Equal Chords Theorem

The converse is also true. If two angles subtended at the center by two chords are equal, then the chords are of equal length.

In the given diagram, the chords XY and ST are equal. Thus, the angles subtended by them are also equal.

∠AOB = ∠POQ

Circle Theorem 7: Cyclic Quadrilateral Theorem

A cyclic quadrilateral is a quadrilateral where all four vertices lie on a circle.

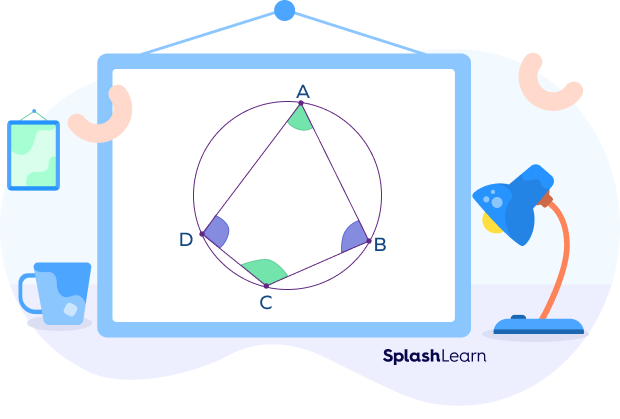
Here, ABCD is a cyclic quadrilateral. According to the cyclic quadrilateral theorem: 

∠A + ∠C = 180⁰ and ∠B + ∠D = 180⁰

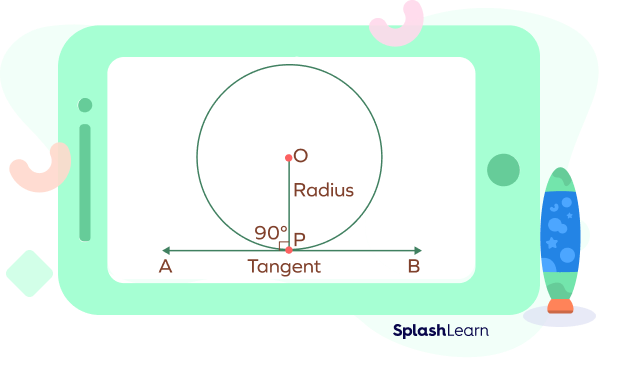
Circle Theorem 8: Tangent of a Circle Theorem-1

In the given diagram, the radius OP is perpendicular to the tangent AB. 

OP ⊥ AB.

∠OPA = ∠OPB = 90⁰.

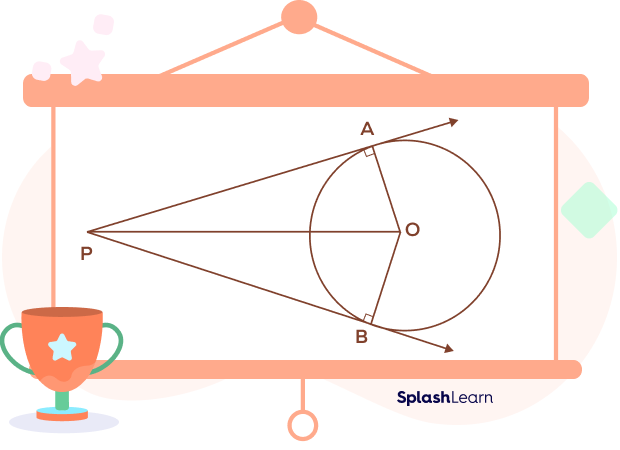
Circle Theorem 9: Two Tangents Theorem

If two tangent lines PA and PB are drawn from an external point, then

• Two tangents have the same length. (PA = PB)
• The two tangents subtend equal angles at the center of the circle. (∠POA = ∠POB)
• The line that connects the exterior point to the center will divide the angle between the tangents into two equal angles. (∠OPA = ∠OPB)

Circle Theorems Formulas

Theorems	Shapes	Formula
Alternate Segment Theorem		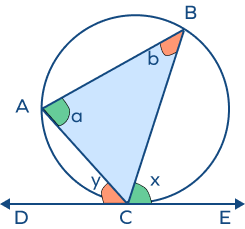∠x = ∠y  and ∠a = ∠b
The central angle subtended by two points on a circle is always twice the inscribed angle subtended by those points.		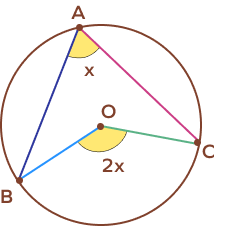∠BOC = 2∠BAC
Angles in the same segment are congruent.		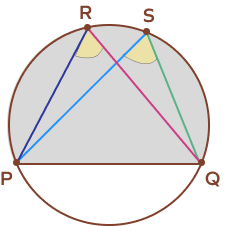∠PRQ = ∠PSQ
Angles in a semicircle are right angles.		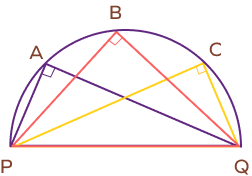∠A = ∠B = ∠C = 900
Chord of a circle theorem		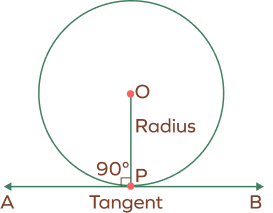AP = PB ∠OPA = ∠OPB = 900
Angles subtended by equal chords		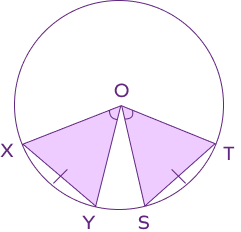∠XOY = ∠SOT
Cyclic quadrilateral theorem		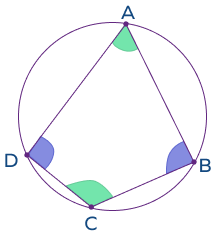∠A + ∠C = 1800 and ∠B + ∠D = 1800
Tangent of a circle theorem-1		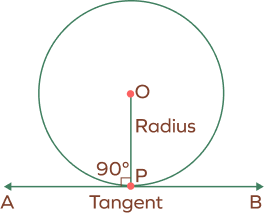∠OPA = ∠OPB = 900
Tangent of a circle theorem-2		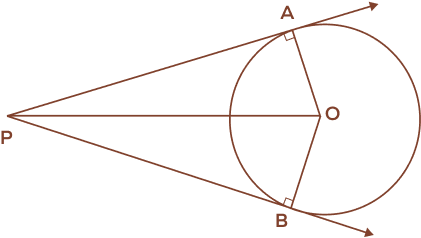PA = PB∠POA = ∠POB∠OPA = ∠OPB

Facts about Circle Theorems

Conclusion

In this article, we delved into the essential circle theorems that provide valuable insights into angles, arcs, and their relationships within a circle. Understanding these theorems is crucial for various geometric applications. Now, let’s reinforce our knowledge by tackling examples and practicing MCQs for better comprehension.

Solved Examples on Circle Theorems

1. In the circle given below, triangle ABC is inscribed in the circle and the tangent DE meets the circle at the point B. Find the measure of angle “x” and “y.”

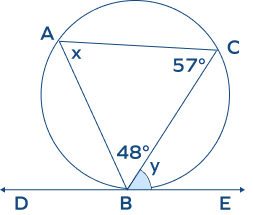
Solution: 

We know that the sum of interior angles of a triangle is equal to 180. 

∠BAC + ∠ACB + ∠ABC = 180⁰

x + 57⁰ +  48⁰ = 180⁰

x = 180⁰ – 105⁰

x = 75⁰

Now, according to the alternate segment theorem, the angle formed between the tangent and the chord through the point of contact of the tangent is equal to the angle formed by the same chord in the alternate segment.

x = y = 75⁰

Hence, the measure of ∠x and ∠y is 75⁰.

2. In the figure given below, find the value of x using the circle theorems.

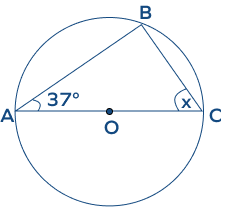
Solution:

In the given figure, ∠ABC is an angle in a semicircle. 

Angle in a semicircle is always a right angle. 

Thus, m∠ABC = 90⁰

We know that the sum of interior angles of a triangle is equal to 180⁰. 

m∠BAC + m∠ACB + m∠ABC = 180⁰

x + 37⁰ + 90⁰ = 180⁰

x + 127⁰ = 180⁰

x = 180⁰ − 127⁰ = 53⁰

Hence, the value of x is 53⁰.

3. In the figure given below, find the value of x using the circle theorems.

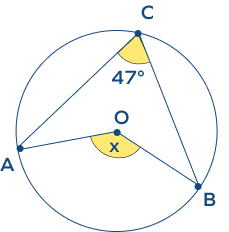
Solution: 

According to “the angle at the center theorem,” the central angle subtended by two points on a circle is always twice the inscribed angle subtended by those points.

∠AOB = 2∠ACB.

x = 2 × 47⁰ = 94⁰

The value of x is 94⁰.

4. In the given figure, the point O is a center of a circle, the radius of a circle is 17 inches and OP = 8 inches. Find the length of the chord AB.

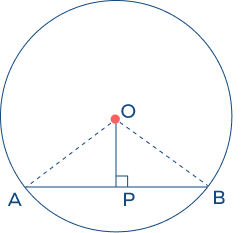
Solution:

In the given figure, 

OA = OB = 17 inches 

OP = 8 inches

OP⊥ AB

Using pythagoras theorem in triangle OPB, we get

OP² + PB² = OB²

8² + PB² = 17²

PB² = 17² − 8² = 225

Therefore, PB = $\sqrt{225}$ = 15 inches

According to the chord of a circle theorem, the perpendicular drawn from the center of the circle bisects the chord.

Thus, AP = PB

∴ AB = AP + PB = 15 inches + 15 inches = 30 inches.

Hence, the length of the chord AB is 30 inches.

5. Find the value of “x” and “y” using the cyclic quadrilateral theorem.

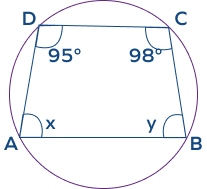
Solution:

In the given figure, ABCD is cyclic quadrilateral. 

We know that the sum of opposite angles in a cyclic quadrilateral is equal to 180⁰.

So, x + 98⁰ = 180⁰

 x = 180⁰ − 98⁰ = 82⁰

Similarly,

y + 95⁰ = 180⁰

 x = 180⁰ − 95⁰ = 85⁰

The values of x and y are 82 and 85 respectively.

6. Find the value of “x” in the figure given below.

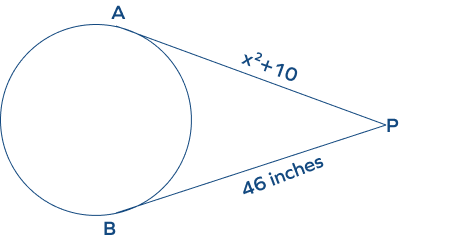
Solution:

Two tangent lines PA and PB are drawn from an external point “P” as shown in the figure, then two tangents have the same length.

Thus, PA = PB.

x² + 10 = 46

x² = 46 − 10

x² = 36

x = 6

Hence, the value of “x” is 6.

Practice Problems on Circle Theorems

Frequently Asked Questions on Circle Theorems