What Is Comparing Ratios in Math?
Comparing ratios means to determine whether one ratio is less than, greater than, or equal to the other ratio. To compare ratios is to evaluate how two or more ratios relate to one another.
A ratio compares two quantities of the same kind. It tells us how much of one quantity is contained in another. It is a comparison of two numbers or amounts a and b, written in the form a : b.
For example, if the ratio of water to milk in a recipe is 1 : 2, it means that the quantity of milk will be exactly twice (double) as compared to the quantity of water.
Example: There are 6 cookies and 4 cupcakes in the given image.
The ratio of cookies to cupcakes in the given image can be expressed in three different ways:
- 6 to 7
- 6 : 7
- $\frac{6}{7}$

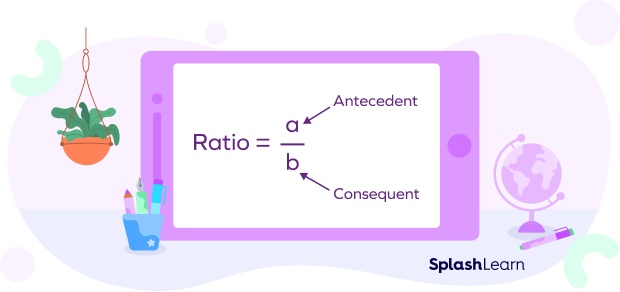
Ratio is the quantitative relationship between two quantities or numbers. In the ratio a : b, the first quantity is called an antecedent and the second quantity is called consequent.
Recommended Games
How to Compare Ratio in Math
Comparing ratios follows a very similar procedure as comparing fractions. Let’s understand the steps.
Step 1: Make sure that the second terms of both ratios are the same.
If the second term is the same, compare the antecedents (numerators).
If it is not the same, find the least common multiple (LCM) of the two consequents. Find the new ratios with the LCM as the common denominator.
Step 2: Compare ratios.
Compare the antecedents (numerators) of the new ratios.
Let’s take an example to understand this better.
Example: Compare the ratios 1 : 5 and 7 : 4. Which one is greater?
1 : 5 and 7 : 4 can be written as $\frac{1}{5}$ and $\frac{7}{4}$ respectively.
LCM(5 and 4) = 20
Now, dividing the LCM by the 2nd term of each ratio, we get 20 ÷ 5 = 4, and 20 ÷ 4 = 5.
Thus, we need to multiply $\frac{1}{5}$ by 4 and $\frac{7}{4}$ by 5 to get the new ratios.
$\frac{1}{5} = \frac{1 \times 4}{5 \times 4} = \frac{4}{20}$ and $\frac{7}{4} = \frac{7 \times 5}{4 \times 5} = \frac{35}{20}$
Numerators of the new ratios are 4 and 35.
$\frac{4}{20} \lt \frac{35}{20}$
Thus, $\frac{1}{5} \lt \frac{7}{4}$
The ratio 7 : 4 is greater than the ratio 1 : 5.
Recommended Worksheets
Methods of Comparing Ratios
Ratio comparison can be done using different methods.
1. LCM method of comparing ratios
2. Comparing ratios by cross multiplication method
3. Converting ratios to decimal numbers
4. Converting ratios to percentages
LCM Method of Comparing Ratios
As discussed earlier, this method is used when the denominators (consequent terms) of the ratios are not the same. If the denominators are the same, simply compare the numerators. If the denominators are different, find the LCM of the denominators. Express the given fractions with the LCM as the common denominator and compare.
Example: Let’s compare the ratios 2 : 3 and 4 : 5 using the LCM method:
Write the ratios in fraction form: $\frac{2}{3}$ and $\frac{4}{5}$.
Find the LCM of the denominators 3 and 5.
LCM(3, 5) = 15.
Rewrite the fractions with the common denominator:
$\frac{2}{3} = \frac{10}{15}$ (multiplied numerator and denominator by 5)
$\frac{4}{5} = \frac{12}{15}$ (multiplied numerator and denominator by 3)
$\frac{10}{15} \lt \frac{12}{15}$
So, the ratio 4 : 5 is larger than the ratio 2 : 3.
Comparing Ratios by Cross Multiplication Method
The cross multiplication method is another way to compare ratios. It involves multiplying the numerator of one ratio by the denominator of the other ratio, and then comparing the results (products).
- If two ratios are equal, then the product after cross multiplication is also equal.
$\frac{a}{b} = \frac{c}{d}$ if $a \times d = b \times c$
Example: $\frac{1}{2} = \frac{2}{4}$ since $4 \times 1 = 2 \times 2$
- $\frac{a}{b} \lt \frac{c}{d}$ if $\frac{a}{d} \lt \frac{b}{c}$.
Example: $\frac{1}{2} \lt \frac{3}{4}$ since $4 \lt 6$
- $\frac{a}{b} \gt \frac{c}{d}$ if $a \times d \gt b \times c$.
Example: $\frac{1}{10} \gt \frac{1}{100}$ since $100 \gt 10$
Comparing Ratios Using Ratio Tables
One way to compare ratios is by using tables. This method proves to be more helpful when comparing more than two ratios. Let’s understand this with the help of an example.
Tabular form allows you to organize the ratios and see the data side by side.
Example 1: Compare the ratios 2 : 3 and 4 : 5 using a table.
Write the given ratios and their equivalent ratios using tables.
| Ratio 2 : 3 | ||||
|---|---|---|---|---|
| 2 | 4 | 6 | 8 | 10 |
| 3 | 6 | 9 | 12 | 15 |
| Ratio 4 : 5 | ||||
|---|---|---|---|---|
| 4 | 8 | 12 | 16 | 20 |
| 5 | 10 | 15 | 20 | 25 |
Identify the equivalent ratio for which the denominators are the same.
$\frac{10}{15} \lt \frac{12}{15}$
Thus, 2 : 3 < 4 : 5
Example 2: Find the unit rate or the unit ratio.
A table showing the number of steps walked by three friends is given below. Who walks the fastest among them?
| Name | Number of steps | Minutes |
|---|---|---|
| Daniel | 900 | 9 |
| Mona | 650 | 5 |
| Kate | 1095 | 15 |
Here, the unit ratio or the unit rate can be defined as the number of steps taken per minute.
To find that, we will divide the number of steps by the number of minutes. Let’s calculate it for each person.
| Name | Number of steps | Minutes | Unit ratio |
|---|---|---|---|
| Daniel | 900 | 9 | 100 : 1 |
| Mona | 650 | 5 | 130 : 1 |
| Kate | 1095 | 15 | 73 : 1 |
Daniel walks 100 steps per minute.
Mona walks 130 steps per minute.
Kate walks 73 steps per minute.
Thus, Mona walks the fastest.
Converting Ratios to Decimal Numbers
We can compare ratios by converting them into decimal numbers. Divide the numerator by the denominator. Find the decimal numbers. Round the decimals if required and compare.
Example: Compare 8 : 5 and 3 : 2.
8 : 5 $= \frac{8}{5} =$ 1.6
3 : 2 $= \frac{3}{2} =$ 1.5
Since 1.5 < 1.6, we can say that 3 : 2 < 8 : 5.
Converting Ratios to Percentages
Here, we convert the ratios into percentages. This is the simplest way to compare ratios. Multiply the given ratio by 100 to find the equivalent value in percentage.
Example: Compare 9 : 10 and 7 : 5.
$\frac{9}{10} \times 100 = 90\%$
$\frac{7}{5} \times 100 = 140\%$
Thus, $\frac{9}{10} \lt \frac{7}{5}$
Facts about Comparing Ratios
- A ratio is a comparison of two quantities of the same kind by using the method of division.
- Ratio is used as a way of explaining the scale factor (how things are enlarged or reduced in size).
- A unit ratio is a ratio of the form a : 1 (a ratio with a second term equal to 1). Every ratio can be converted to a unit ratio.
- Comparing ratios can also be used in art and design. For example, the golden ratio (1.618) is often used in design and architecture to create visually pleasing artwork.
- Comparing ratios can be useful in cooking and baking. For example, a recipe may call for a ratio of flour to sugar, and comparing different recipes can help you determine which one has the right ratio for your tastes.
- To compare quantities using ratios, the quantities must be expressed in the same unit.
- A ratio has no unit since the units get canceled out.
- The order is very important in a ratio. For instance, the ratio a : b and the ratio b : a are very different.
- The ratio of the circumference of a circle to its diameter is always the same, regardless of the size of the circle. This constant ratio is known as pi (π).
- If the first term is greater than the second term, the ratio is greater than 1. Moreover, if the ratio is lower than 1, the second number will be greater than the first.
Conclusion
In this article, we have studied about comparison of ratios and methods of comparison of ratios. Let’s solve some examples on ratio comparisons to understand the concept better.
Solved Examples on Comparing Ratios
1. Compare the ratios 3 : 5 and 2 : 7 using the LCM method.
Solution:
To compare the ratios, we need to find a common denominator. The LCM of 5 and 7 is 35. We can rewrite the ratios as follows:
$\frac{3}{5} = \frac{3\times 7}{5 \times7} = \frac{21}{35}$
$\frac{2}{7} = \frac{2 \times 5}{7 \times 5} = \frac{10}{35}$
$\frac{3}{5} = \frac{21}{35} \lt \frac{2}{7} = \frac{10}{35}$
Therefore, the ratio 3 : 5 is larger than the ratio 2 : 7.
2. Compare the ratios 4 : 5 and 6 : 7 using the cross-multiplication method.
Solution:
4 : $5 = \frac{4}{5}$
6 : $7 = \frac{6}{7}$
Multiply the numerator of the first ratio by the denominator of the second ratio. Similarly, find the product of the numerator of the second ratio and the denominator of the first ratio. If the first product is larger, then the first ratio is larger. If the second product is larger, then the second ratio is larger.
$\frac{4}{5}$ ? \frac{6}{7}$
$4 \times 7 = 28$
$6 \times 5 = 30$
Since 28 < 30, the ratio 4 : 5 is less than the ratio 6 : 7.
3. Compare the ratios 2 : 3 and 8 : 11 by converting them into percentages.
Solution:
Let’s convert the ratios to percentages.
$\frac{2}{3} \times 100 = 66.67\%$
$\frac{8}{11} \times 100 = 72.72\%$
$72.72\% \gt 66.66\%$
Therefore, 8:11 > 2:3.
4. The information about the number of math problems solved by three students is given below. Who has solved the maximum number of problems in one minute?
| Name of student | Number of math problems | Time (in minutes) |
|---|---|---|
| Alex | 64 | 8 |
| Holden | 55 | 5 |
| Jim | 39 | 3 |
Solution:
Let’s find the unit rate to find the number of problems solved by each student in one minute.
| Name of student | Number of math problems | Time (in minutes) | Unit ratio |
|---|---|---|---|
| Alex | 64 | 8 | 8 : 1 |
| Holden | 55 | 5 | 11 : 1 |
| Jim | 39 | 3 | 13 : 1 |
Alex solves 8 problems in one minute.
Holden solves 11 problems in one minute.
Jim solves 13 problems in one minute.
Thus, Jim has the fastest rate in solving math problems.
Practice Problems on Comparing Ratios
Comparing Ratios: Definition, Methods, Facts, Examples, FAQs
7 : 12 ____ 35 : 60
35 : 60 is the equivalent ratio of 7 : 12
Thus, 7 : 12 = 35 : 60
What is the LCM method used for when comparing ratios?
The LCM (least common multiple) method of comparing ratios involves finding the least common multiple of the denominators of the ratios, and then comparing the corresponding numerators.
If $\frac{a}{b} = \frac{c}{d}$, then
If ab=cd, then ad = bc.
Find the missing number: $\frac{3}{5} = \frac{?}{10}$
$\frac{3 \times 2}{5 \times 2} = \frac{6}{10}$
Alternatively, we can also use cross-multiplication.
$\frac{3}{5} = \frac{?}{10}$
$30 = 5 \times ?$
$? = 6$
Thus, the missing number is 6.
The ratio 35 : 84 in simplest form is
$\frac{35 \div 7}{84 \div 7} = \frac{5}{12}$
Frequently Asked Questions on Comparing Ratios
How to determine which ratio is greater?
To determine which ratio is greater, you can use different methods such as the LCM method, the cross-multiplication method, or you can convert them into decimals or percentages. By using these methods, you can compare the two ratios and determine which one is larger.
How can we find the ratio of two numbers?
To find the ratio of two numbers, you can divide one number by the other. The resulting quotient will give you the ratio of the two numbers. For example, if you want to find the ratio of 6 and 3, you would divide 6 by 3, which gives you 2. Therefore, the ratio of 6 to 3 is 2:1 or $\frac{2}{1}$.
Can ratios be compared if the quantities have different units?
No, ratios cannot be compared if the quantities have different units. The quantities being compared must have the same units in order to be compared.
What is the purpose of comparing ratios?
Comparing ratios allows you to see how two or more quantities relate to each other in relation to another. It tells you how much of one quantity is contained in the other quantity.































