What Are Concave Polygons?
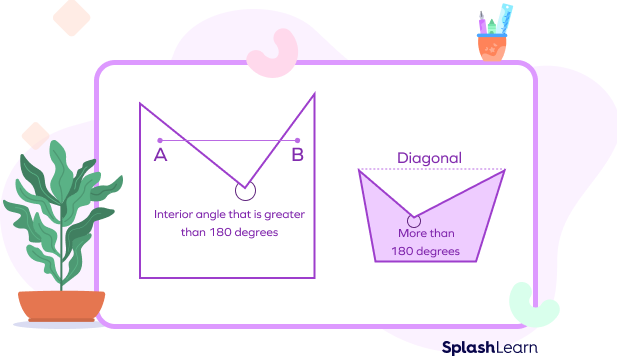
A concave polygon is a polygon in which at least one interior angle is a reflex angle (angle greater than 180° but less than 360°).
A concave polygon has at least 4 sides. It means that a triangle is always a convex polygon. The diagonals in a concave polygon may lie partly or fully outside the polygon.
Since the interior angles are not equal, all concave polygons are “irregular polygons.” If you connect any two points inside or on the polygon by a straight line, and it goes outside the polygon, then the polygon is concave.
In geometry, a polygon can be defined as a flat or plane, two-dimensional closed shape, bounded with straight sides. It does not have curved edges. There are two types of polygons based on the measure of interior angles.
- Convex Polygons
- Concave Polygons
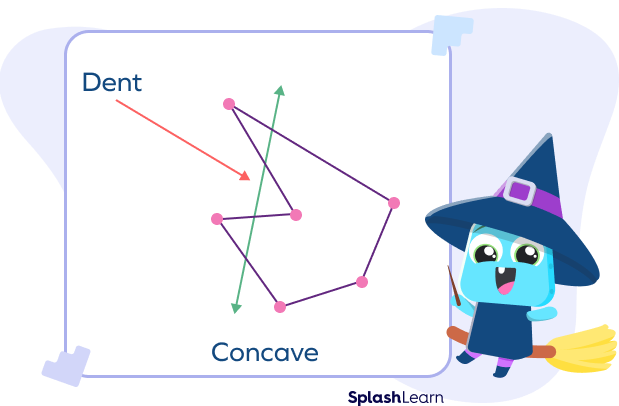
The term “concave” refers to a shape having an outline or surface that curves inwards. Concave polygons have dents. Take a look at a few examples of concave polygons.

Recommended Games
Concave Polygon: Definition
If the measure of at least one interior angle of a polygon is greater than 180 degrees, the polygon is said to be a concave polygon.
Properties of Concave Polygon
- There is at least one angle in a concave polygon which is a reflex angle (greater than 180° and less than 360°).
- One or more diagonals in a concave polygon are partly or fully outside.
- There is at least one vertex in a concave polygon that seems to be pushed inwards to give that distinct “cave” shape or dented shape to the polygon.
- If we draw a line segment across a concave polygon, it touches more than 2 sides.
- Concave polygons are irregular polygons.
Concave Polygon vs. Convex Polygon
| Convex Polygons | Concave Polygons |
|---|---|
| All interior angles are less than 180°. | It has at least one interior angle greater than 180° (reflex). |
| The minimum number of sides of a convex polygon is 3. | The minimum number of sides of a concave polygon is 4. |
| When we draw a line inside a convex shape from any one side, it touches only 2 sides. | When we draw a line inside a concave shape from one side, it touches more than 2 sides. |
| The diagonals in a convex polygon do not lie outside the polygon. | One or more diagonals in a concave polygon are partly or fully outside it. |
Angles in a Concave Polygon
Let’s discuss formulas for the sum of interior angles and the sum of exterior angles in a concave polygon.
- Sum of Exterior Angles of a Concave Polygon
Like any other polygon, the sum of the exterior angles of a concave polygon is 360°. This means the exterior angles always add up to 360° for all concave polygons.
- Sum of Interior Angles of a Concave Polygon
To find the sum of interior angles of a concave polygon, we use the same formula that is applied for any other polygon.
Sum of interior angles = (n – 2) × 180°, where “n” is the number of sides of a polygon.
Concave Polygon Formulas
Let’s understand how to find the area and perimeter of a concave polygon.
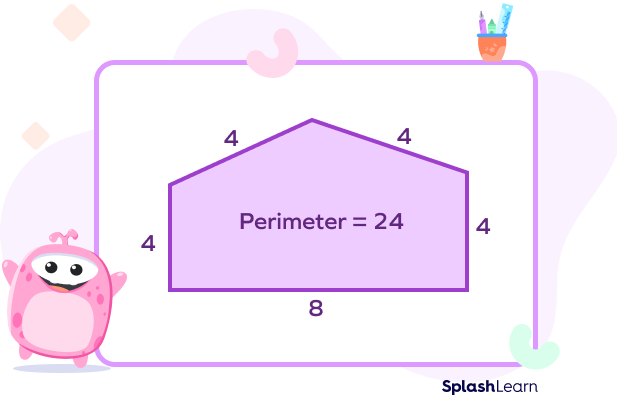
- Perimeter of a Concave Polygon
Perimeter of a concave polygon is simply the total length of its outer boundary. To find the perimeter of a concave polygon, simply add the length of all its sides.
Example: The perimeter of the given polygon is 4 + 4 + 4 + 4 + 8 = 24 units
- Area of a Concave Polygon
Concave polygons are irregular polygons. Thus, to find the area of a concave polygon, we simply break it into the shapes whose area can be calculated with a formula.
Example: The area of the given polygon is simply the sum of the area of the four triangles.

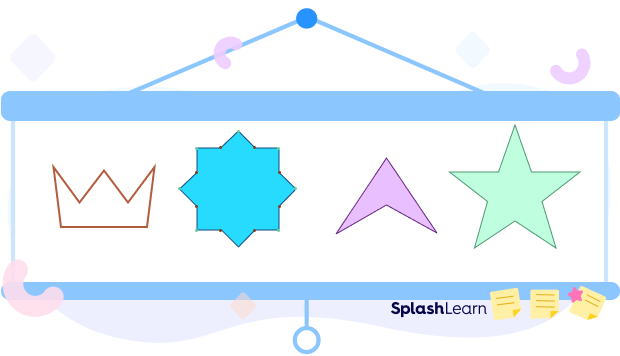
Concave Polygons in Real Life
Concave polygons have a peculiar shape in which at least one of the vertices is pointed inwards. We can notice concave polygons in our day-to-day life. Let’s take a look at convex and concave shapes around us.
- Concave polygon shapes:
Solved Examples on Concave Polygons
1. If the number of sides of a concave polygon is 5, then what will be the sum of its interior angles?
Solution:
Number of sides = n = 5
Sum of interior angles = (n – 2) × 180°
=(5 – 2) × 180°
=3 × 180°
= 540°
2. Which of the following are concave polygons?

Solution:
Concave polygons have a dent or a vertex turned inwards. At least one interior angle measures greater than 180 degrees.
Concave Polygons: B, E, F
Convex Polygons: A, C, D
3. Find the value of the interior angle ∠E.
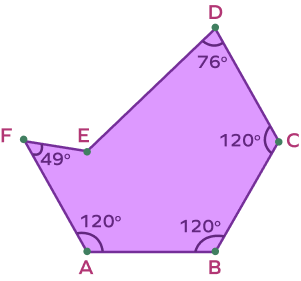
Solution:
n=6
Sum of interior angles = (n-2) × 180°
= (6-2) × 180°
= 4 × 180°
= 720°
In hexagon ABCDEF,
m∠A + m∠B + m∠C + m∠D + m∠E + m∠F = 720°
m∠E + 49° + 120° + 120° + 120° + 76° = 720°
m∠E + 485° = 720°
m∠E = 720°-485°
m∠E =235°
4. Find the perimeter of the given convex polygon.
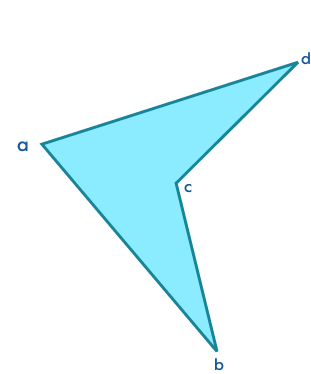
Solution:
Perimeter is the total length of the outer boundary.
Thus, perimeter of the given polygon = (a + b + c + d) units
5. Fill in the blanks with the correct word.
(a) In a _____ polygon, at least one angle is greater than 180°.
(b) A polygon with all interior angles less than 180° is a ____ polygon.
(c) The sum of the exterior angles of a concave polygon is _____.
Solution:
(a) In a concave polygon, at least one angle is greater than 180°.
(b) A polygon with all interior angles less than 180° is a convex polygon.
(c) The sum of the exterior angles of a concave polygon is 360o.
Practice Problems on Concave Polygons
Concave Polygon - Definition, Types, Properties, Examples, FAQs
Which of the following is NOT a concave polygon?
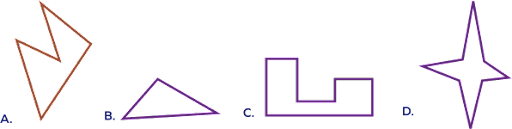
A triangle is always a convex polygon. The sum of angles in a triangle is 180 degrees. So, a triangle can never be a concave polygon.
Which of the following is a property of a concave polygon?
A, B and C are not the properties of a concave polygon. One or more diagonals lie outside the polygon. The sum of interior angles of a concave polygon is $(n \;-\; 2) \times 180^{\circ}$
The minimum number of sides of a concave polygon is _______.
The minimum number of sides of a concave polygon is 4.
Which of the following shapes represent a concave polygon?
A star is a concave shape.
One or more diagonals of a concave polygon lie _______ the polygon.
Some diagonals of a concave polygon lie outside the polygon.
Regular polygons can never be _____.
Regular polygons can never be concave. All the concave polygons are irregular polygons.
Frequently Asked Questions about Concave Polygons
How can we find the perimeter of a concave polygon?
The perimeter of a concave polygon is calculated in the same way as the perimeter of convex polygons. All the sides of the polygon are added to find the perimeter.
How can we find the area of a concave polygon?
Concave polygons are irregular in shape. A concave polygon can be divided into triangles or other smaller polygons. Then, the area of these shapes can be calculated with the appropriate formulas and these areas can be added together to get the area of the concave polygon.
Why is an arrow a concave polygon?
An arrow is a concave polygon because it fulfills all the conditions of a concave polygon. It has interior angles that measure more than 180° and one diagonal in an arrow lies outside the shape.
What is the difference between a regular polygon and a concave polygon?
A regular polygon is a polygon that is equilateral and equiangular whereas a concave polygon is a polygon in which at least one angle is more than 180°.
Is a triangle a concave polygon?
No, a triangle is not a concave polygon as there are no diagonals in a triangle. Also, the sum of angles of a triangle is 180°.
Is a star a concave polygon?
A star is a concave polygon.


















