Construct an Angle Bisector – Definition, Examples, FAQs

What Is Meant by Constructing Angle Bisectors?

Constructing an angle bisector simply means constructing a line that divides a given angle into two equal parts. In other words, it refers to constructing or drawing a line that bisects a given angle.

An angle is formed when two rays meet at a point called a vertex. An angle bisector is a line that divides an angle into two equal halves. 

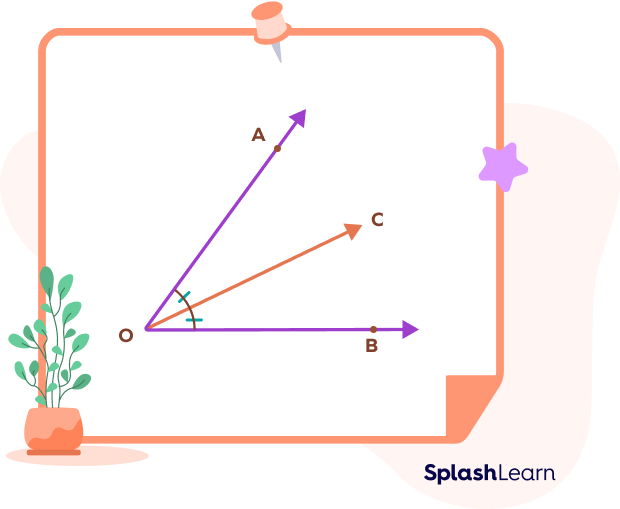
In the figure given above, OC is an angle bisector of $\angle AOB$.

It means $\angle AOC = \angle BOC = 12 \angle AOB$

Suppose an angle bisector is constructed for an angle of 80 degree, it divides the angle into two equal angles of 40 degrees each. We can construct angle bisectors for all types of angles, such as acute angles, obtuse angles, or right angles.

Which Tools Are Necessary to Construct an Angle Bisector?

You might need to grab the following tools to draw an angle bisector.

• A ruler 
• A pencil
• A compass
• A protractor 

How to Construct an Angle Bisector With a Compass

Let’s understand how to bisect an angle with a compass.

Suppose that we have to construct an angle bisector for the angle POQ shown below.

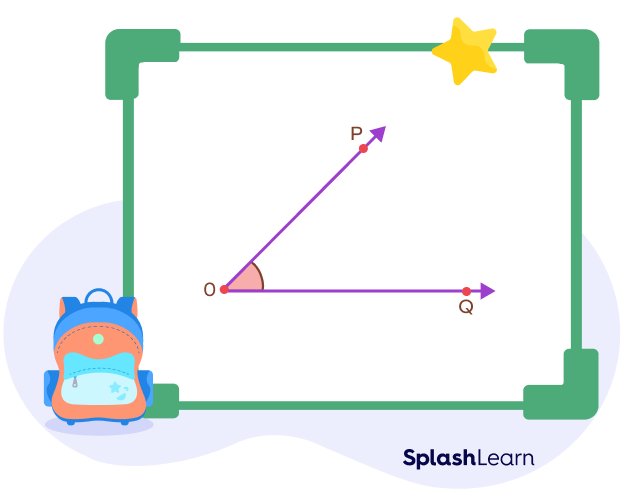
Step 1: Open the compass to any suitable distance. Keeping Y as the center, draw an arc such that it cuts the arms of the angle at points X and Y respectively.

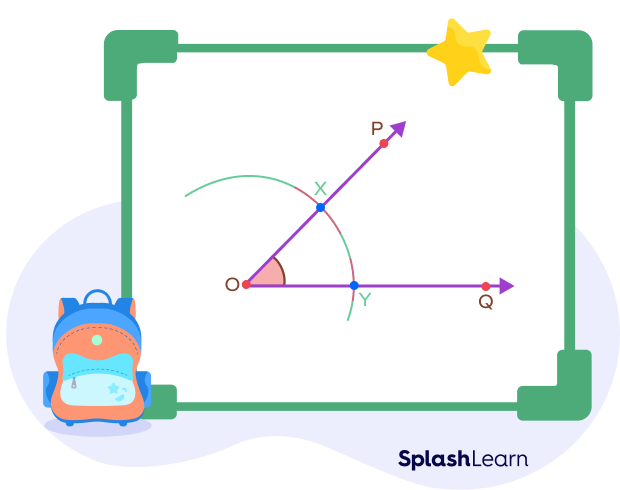
Note: $OX = OY$, since these are drawn keeping the same radii on the compass.

Step 2: Using the same distance on the compass, draw two arcs with X and Y as centers. Let these two arcs intersect at a point named Z.

Since we did not change the radius of the compass, we have $XZ = YZ = OX = OY$.

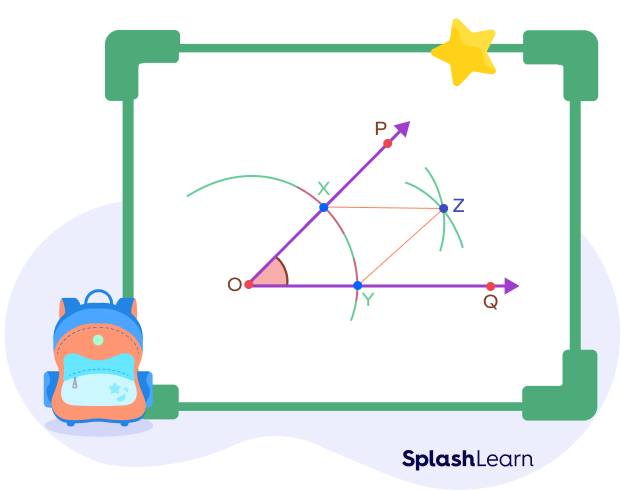
Step 3: Join the points O and Z. OZ is the required angle bisector of angle POQ.

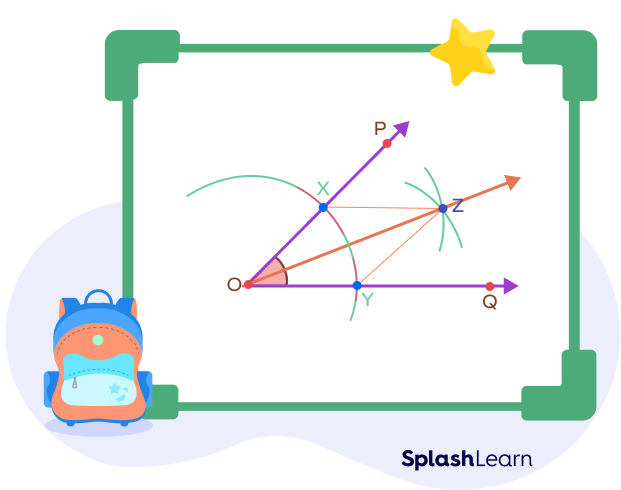
How to Prove That a Line Is an Angle Bisector

We will refer to the previous diagram. Let us prove that XZ is the angle bisector of the angle POQ (angle XOY).

In $\Delta OXZ$ and $\Delta OYZ$,

$XZ = YZ$ (arcs drawn with equal radii)

$OX = OY$ (arcs drawn with equal radii)

$OZ = OZ$ (common side)

By the SSS criterion, $\Delta OXZ$ and $\Delta OYZ$ are congruent. 

$\Delta XOZ = \Delta YOZ$ (Corresponding parts of congruent triangles)

Thus, ray OZ is the angle bisector of $\Delta XOY$ or $\Delta POQ$.

How to Construct an Angle Bisector with a Protractor

Step 1: Align the initial arm of the angle with the baseline of the protractor such that the vertex is on the center of the protractor.

Step 2: Note down the measure of the given angle. 

Divide it by 2.

Step 3: Mark this measurement on the protractor.

Step 4: Join the center of the protractor with the marked point.

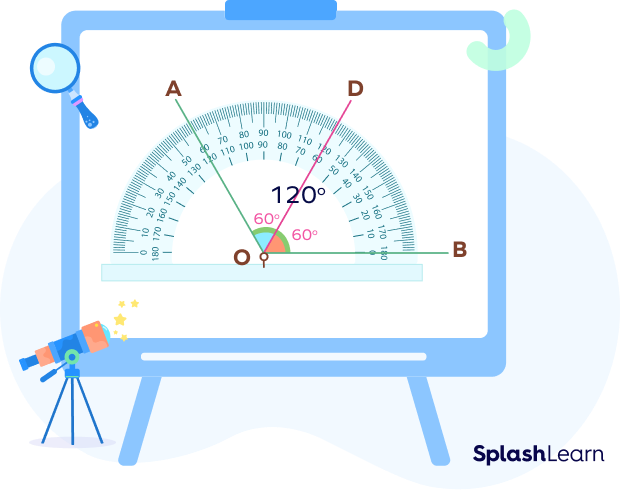
Properties of an Angle Bisector

• An angle bisector divides an angle into two equal angles.
• Any point on the angle bisector is at an equal distance from the arms or sides of the angle.
• The angle bisector in a triangle divides the opposite side in a ratio that is equal to the ratio of the other two sides.

Conclusion

In this article, we learned how to construct an angle bisector. We explored the method step by step with the help of examples. Let’s solve a few examples and practice problems to check our understanding of these concepts.

Solved Examples on Construction of Angle Bisectors

1. Identify the steps used to draw an angle bisector OC in the given diagram. Also, based on the construction of an angle bisector, which line segments and angles must be congruent? 

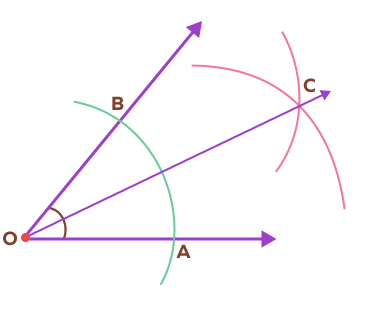
Solution:

Here, $\Delta AOB$ is given. 

Step 1: In the first step, an arc is drawn keeping O as center with a suitable radius in the compass. It cuts the arms of the angle at A and B.

Thus, $OA = OB$

Step 2: Next, without changing the radius of the compass, we draw two arcs keeping A and B as centers, which intersect each other at the point C. 

Thus, $AC = BC$.

Step 3: The line segment OC, joining O and C is the angle bisector.

$\Delta AOC = \Delta BOC = \frac{1}{2} \Delta AOB$

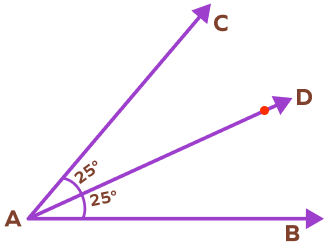
2. How can you draw the angle bisector of $50^{\circ}$ with a protractor?

Solution:

Draw a baseline AB. Put the center of the protractor on the point A.

Now, we will mark two points using the inner calibration of the protractor.

First, mark a point C representing the 50 degree angle.

Next, mark a point D representing the 25 degree angle since it is exactly half of 50 degrees.

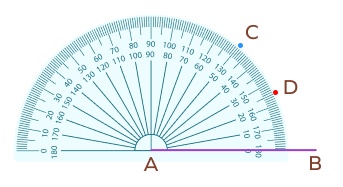
Remove the protractor. Join points A and C. Join the points A and D.

Here, AD is the angle bisector of $\angle BAC$.

$\angle BAD = \angle CAD = \frac{1}{2} \angle BAC = 25^{\circ}$

$\angle BAC = 50^\circ$

3. Find the value of x if OM is an angle bisector.

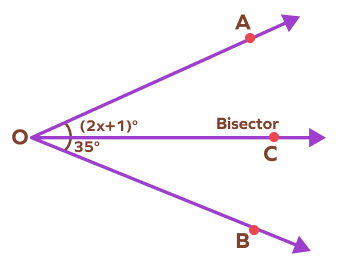
Solution: 

Since OM is an angle bisector, the angles BOC and AOC are equal.

$2x + 1 = 35$

$2x = 34$

$x = 17$

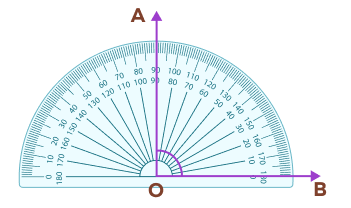
4. Draw a right angle using a protractor and bisect it using a compass.

Solution:

First, draw a right angle using a protractor. Draw a baseline OB. Using the inner calibration, mark the point showing 90 degrees. Join the origin and the marked point.

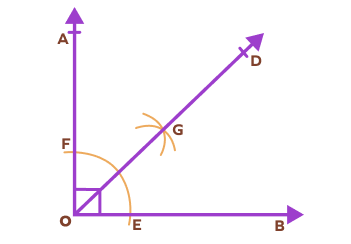
Keeping the center as O and with a suitable radius, draw an arc that meets OB at E and OA at F. Using the same radius in the compass, draw two arcs in the interior of the angle keeping E and F as centers that will intersect at point G. Join OG. OG is the angle bisector of a right angle. 

$\angle AOG = \angle BOG = \frac{1}{2} \angle AOB = 45^{\circ}$

Practice Problems on Construction of Angle Bisectors

Frequently Asked Questions on Construction of Angle Bisectors