Intercept Form – Definition, Equation, Formula, Examples, FAQs

What Is Intercept Form?

The intercept form of a line is a specific representation of the equation of a straight line using its x-intercept and y-intercept. The intercept form is often referred to as the two-intercept form because it involves the x-intercept and y-intercept of the line.

If we have the x-intercept (a, 0) and the y-intercept (0, b) of a line, we can write the equation in the two-intercept form as:

$\frac{x}{a} + \frac{y}{b} = 1$

In this equation:

• ‘a’ represents the x-intercept, which is the value of x when y = 0 (the point where the line intersects the X-axis).
• ‘b’ represents the y-intercept, which is the value of y when x = 0 (the point where the line intersects the Y-axis).

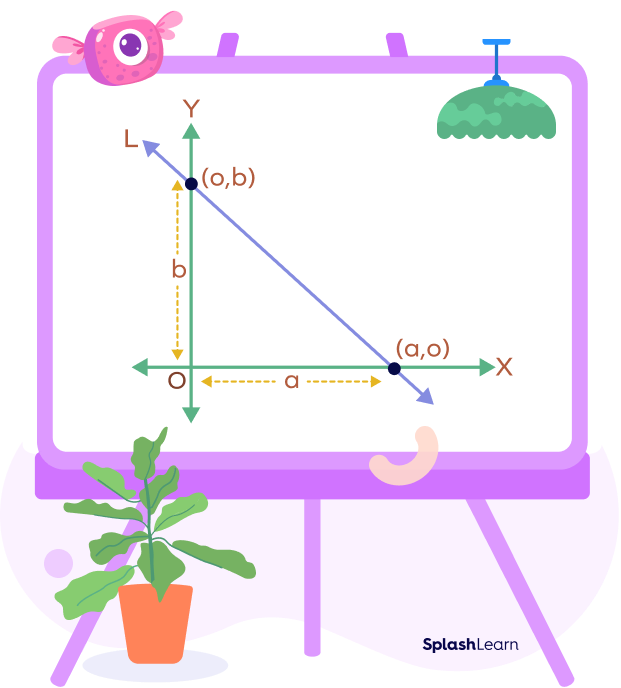
By observing the coefficients ‘a’ and ‘b’ in the intercept form equation, you can easily determine the x-intercept and y-intercept of the line. The x-intercept is (a, 0), and the Y-intercept is (0, b) which means the line cuts the X-axis at the point (a, 0), and it cuts the Y-axis at the point(0, b).

Intercept Form: Definition

The two-intercept form of the equation of a straight line that intersects the X-axis at (𝑎,0) and the Y-axis at (0,𝑏) is

$\frac{x}{a} + \frac{y}{b} = 1$

The intercept form allows us to visualize the position of the line and its relationship with the coordinate axes based on the signs of the intercepts.

Intercept Form Formula

In this formula,

• ‘a’ represents the x-intercept
• ‘b’ represents the y-intercept

The intercept form formula provides a straightforward and concise way to express the equation of a line using its intercepts. By substituting the appropriate values of ‘a’ and ‘b’, you can write the equation of a line in the intercept form.

How to Find Intercept Form

To find the intercept form of the equation of a line, you typically need information about the intercepts of the line, such as the x-intercept and y-intercept.

If you have the x-intercept (a, 0) and the y-intercept (0, b) of the line, you can follow these steps to determine the intercept form:

Step 1: Identify the x-intercept and y-intercept values. 

a = x-intercept, b = y-intercept

Step 2: Use the intercept values in the intercept form equation, which is given by

$\frac{x}{a} + \frac{y}{b} = 1$.

Step 3: Substitute ‘a’ for the x-intercept and ‘b’ for the y-intercept in the equation. This gives you the equation in the intercept form.

Example: x-intercept is 4 and the y-intercept is 2. Find the intercept form.

We can substitute these values into the intercept form equation:

$\frac{x}{4} + \frac{y}{2} = 1$

Simplifying further, you can multiply through by the common denominator to eliminate fractions:

$\frac{2x}{8} + \frac{4y}{8} = 1$

Thus, $2x + 4y = 8$

This is the intercept form equation of the line.

Graph of Intercept Form of Equation of a Line

The graph of the intercept form equation $\frac{x}{a} + \frac{y}{b} = 1$ is a straight line that intersects the X-axis at the x-intercept (a, 0) and the Y-axis at the y-intercept (0, b).

The two points are situated on the X-axis and Y-axis, respectively, and are separated by ‘a’ and ‘b’ units from the origin.

The line passes through the point (a, 0) on the X-axis because it has an intercept of ‘a’ units on the X-axis. It passes through the point (0, b) on the Y-axis and makes an intercept of ‘b’ units on the Y-axis.

Intercept form equation: $\frac{x}{a} + \frac{y}{b} = 1$

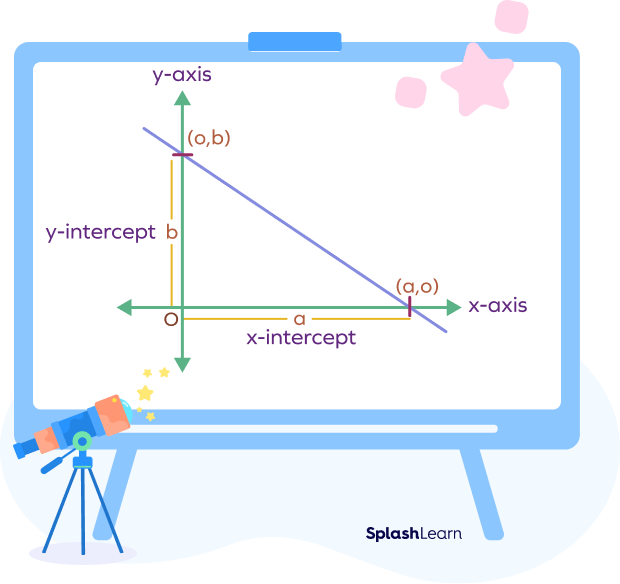
Derivation of Intercept Form of Equation

The intercept form can be obtained by rearranging and manipulating the equations, which are used in other forms of equations of a line, specifically the two-point form.

Here, we will derive the intercept form of the equation of a line from the two-point form of the equation.

The two-point form of the equation of a line relies on having two points on the line. By using the coordinates of the two given points (a, 0) and (0, b), we can determine the equation of the line passing through them. The equation for this line, which passes through (a, 0) and (0, b) respectively, is as follows:

$y − 0 = \frac{(b − 0)}{(0 − a)} \times (x − a)$

$y = \frac{b}{− a} (x − a)$

$− ay = b(x − a)$

$− ay = bx − ab$

$ab = bx + ay$

$bx + ay = ab$

$\frac{(bx + ay)}{ab} = 1$

$\frac{bx}{ab} + \frac{ay}{ab} = 1$

$\frac{x}{a} + \frac{y}{b} = 1$

Facts about Intercept Form

Conclusion

In this article, we learned about the intercept form of the equation of a line. The intercept form is a representation of the equation of a straight line using its two intercepts. Now, let’s solve some examples and practice problems to understand the concept better!

Solved Examples on Intercept Form

Example 1: Find the equation of a line with an x-intercept of 4 and a y-intercept of –3 in the intercept form.

Solution: 

The x-intercept is 4. 

a = 4

The y-intercept is − 3.

b = − 3

Using these points, we can set up the intercept form equation:  

$\frac{x}{a} + \frac{y}{b} = 1$

Substituting the x-intercept and y-intercept values, we get: 

$\frac{x}{4} + \frac{y}{(− 3)} = 1$ 

On simplifying further, we can write

$3x − 4y = 12$

Example 2:The equation of a line is $\frac{2x}{5} − \frac{3y}{7} = 1$. Find the x-intercept and y-intercept.

Solution:

To find the x-intercept, we set y = 0 and solve for x: 

$\frac{2x}{5} − \frac{3(0)}{7} = 1$

$\frac{2x}{5} = 1$

$2x = 5$

$x = \frac{5}{2}$

So, the x-intercept is $(\frac{5}{2},\; 0)$.

To find the y-intercept, we set x = 0 and solve for y:

$\frac{2(0)}{5} − \frac{3y}{7} = 1$ 

$\frac{− 3y}{7} = 1$ 

$− 3y = 7$

$y = \frac{− 7}{3}$

So, the y-intercept is $(0,\; \frac{−7}{3})$.

Therefore, the x-intercept is $(\frac{5}{2},\; 0)$ and the y-intercept is $(0,\; \frac{−7}{3})$.

Example 3: Find the equation of a line with the x-intercept at (5, 0) and passing through the point (2, 3) in the intercept form.

Solution:

To find the y-intercept, we can use the x-intercept. 

The x-intercept is (5, 0), which means a = 5.

To find the y-intercept, we use the point (2, 3). 

We substitute the coordinates (5, 0) into the equation and solve for b:

$\frac{2}{5} + \frac{3}{b} = 1$ 

$\frac{3}{b} = 1 − \frac{2}{5}$

$\frac{3}{b} = \frac{3}{5}$

$b = 5$

Therefore, the equation of the line in the intercept form is: 

$\frac{x}{5} + \frac{y}{5} = 1$ 

$x + y = 5$

Example 4: Write the equation of the line $y = − 2x + 6$ in the intercept form.

Solution: 

The equation of this line has been given in slope–intercept form 𝑦 = 𝑚𝑥 + 𝑏, where 𝑚 represents the slope of the line and 𝑏 represents the 𝑦-intercept. 

We know that the intercept form of the equation of a straight line is $\frac{x}{a} + \frac{y}{b} = 1$

Add 2𝑥 to each side of the equation $y = − 2x + 6$

$y + 2x = − 2x + 6 + 2x$

Thus, $2x + y = 6$

For any equation of a straight line to be in the intercept form, the constant term must be equal to 1. 

Divide both sides of the equation by 6.

$\frac{2x}{6} + \frac{y}{6} = 1$

 $\frac{x}{3} + \frac{y}{6} = 1$

Thus, the equation of the line $y = −2x + 6$ in the intercept form is $\frac{x}{3} + \frac{y}{6} = 1$

Practice Problems on Intercept Form

Frequently Asked Questions about Intercept Form