Inverse Function – Definition, Types, Examples, Facts, FAQs

What Is an Inverse Function?

The inverse function $f^{-1}$ undoes the action performed by the function f.  We read $f^{-1}$ as “f inverse.”

If $f^{-1}$ is an inverse of the function f, then f is an inverse function of $f^{-1}$. Thus, we can say that  f and $f^{-1}$ reverse each other.

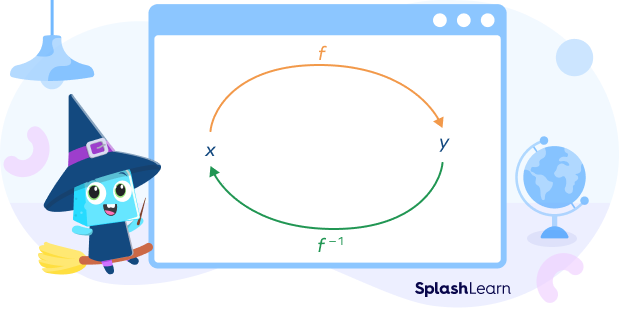
A function from set A to the set B, represented by $f:A \rightarrow B$ is a relation from the set A (a set of inputs) to the set B (a set of possible outputs) such that every element in A is related to exactly one element from the set B. 

Domain: The set of inputs/ the set of values for which the function is defined/ the set of values that we can plug into the function

Range: The set of outputs/ the set of resulting values 

The symbol for inverse function is $f^{-}1\; (f$ with the exponent of $\;﹣\;1)$. 

Inverse Function Definition in Math

A function $g = f^{-1}$ is said to be an inverse function of a function $y = f(x)$ if whenever $f(x) = y$, we have $g(y) = f^{-1}(y) = x$.  If f and g are inverse functions, then we have $f(x) = y$ if and only if $g(y) = x$.

Inverse Function Formula

If f maps x to $f(x)$, then $f^{-1}$ maps f(x) back to x. Thus, if you apply a function and then its inverse, you get the original value. Same applies if we reverse the order of the two functions. Thus, the inverse function formula can be given as

$f^{-1}(f(x)) = x$  …for all x in the domain of f

and

 $f(f^{-1}(y))=y$ …for all y in the domain of $f^{-1}$

If domain $=$ range, we can say that

$f^{-1}(f(x)) = f(f^{-1}(x)) = x$

$f^{-1}$ Meaning and Mapping Diagram

Consider a mapping diagram of a function f and its inverse $f^{-1}$ . 

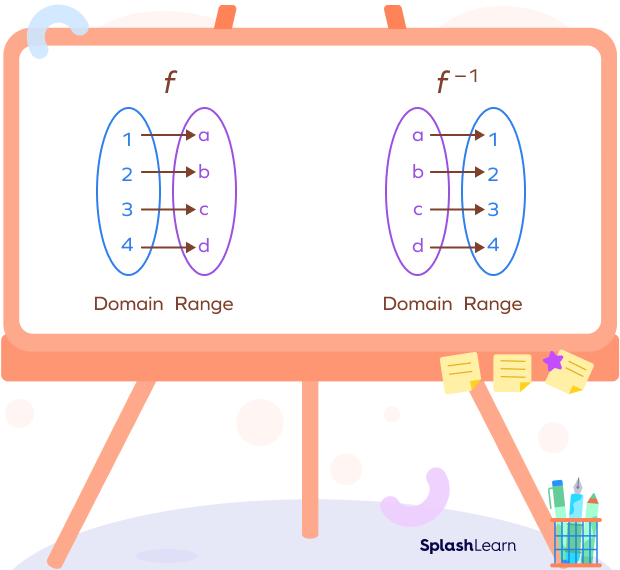
What do you notice?

The domain of f is the range of $f^{-1}$.

The domain of $f^{-1}$ is the range of f.

Action of the function  f	Action of the inverse function $f^{-1}$
f takes 1 to a.	$f^{-1}$ takes a to 1.
f takes 2 to b.	$f^{-1}$ takes b to 2.
f takes 3 to c.	$f^{-1}$  takes c to 3.
f takes 3 to d.	$f^{-1}$  takes d to 4.

How to Find the Inverse of a Function

Let’s understand the steps to find the inverse of a function with an example.

Let us consider a function $f(x) = ax + b$.

Step 1: For the given function, replace $f(x)$ by y. In other words, substitute $f(x) = y$.

Put $f(x) = y$ in $f(x) = ax + b$. 

The result is $y = ax + b$.

Step 2:  Replace x with y. Replace y with x. 

 In the function $y = ax + b$, we interchange x and y.

The result is $x = ay + b$.

Step 3: Solve the expression to write it in terms of y.

$x = ay + b \Rightarrow y = $\frac{x \;-\; b}{a}$

The result is $y = \frac{x \;-\; b}{a}$

Step 4: Replace $y = f^{-1}(x)$.

The result is $f^{-1}(x) = \frac{x \;-\; ba}$.

Thus, $f ^{-1}(x)= \frac{x \;-\; b}{a} is an inverse function of $y = f(x) = ax + b$.

Inverses of Some Common Functions

Some common inverse functions are given below:

Function	Inverse Function	Conditions
$ax + b$	$x \;-\; ba$	$a \neq 0$
$\frac{1}{x}$	$\frac{1}{y}$	x and y not equal to 0
$x^2$	$\sqrt{y}$	$x$ and $y ≥ 0$
$e^x$	ln(y)	$y > 0$
sin(x)	$sin^{-1}(y)$	$\frac{-\pi}{2}$ to $\frac{-\pi}{2}$
cos(x)	$cos^{-1}(y)$	0 to
tan(x)	$tan^{-1}(y)$	$\frac{\pi-}{2}$ to $\frac{-\pi}{2}$

Does Every Function Have an Inverse?

Not every function has an inverse. A function has an inverse if and only if it is one-to-one (or bijective). A function f has an inverse function if and only if, for every element y in its range, there is only one value of x in its domain for which $f(x) = y$. 

It means that for each output, there is precisely only one input. The function does not take the same value twice. In other words, a function f is one-to-one if, for every a and b in its domain, $f(a) = f(b)$ implies $a = b$.

Inverse Function Graph

The graphs of f and $f\;-\;1$are symmetric over the line $x = y$. The functions f and $f\;-\;1$ are mirror images of each other on a graph since the roles of these two variables are reversed. Thus, we can identify whether two functions are inverses of each other simply by checking if they are symmetric over $x = y$.

What Are the Types of Inverse Functions?

The different types of inverse functions include inverse trigonometric functions, inverse of rational functions, inverse hyperbolic functions, and inverse of logarithmic functions.

Inverse of Rational Functions

A rational function is an algebraic function such that both numerators and denominators are polynomials. It is a function of the form $f(x) = \frac{P(x)}{Q(x)}$ where $Q(x) \neq 0$. 

The steps to find the inverse of a rational function are:

Step 1: Substitute $f(x) = y$.

Step 2: Interchange x and y.

Step 3: Solve for y and express it in terms of x.

Step 4: Replace y with $f^{-1}(x)$. 

The final result we get is the inverse function. 

Example: Find the inverse of $f(x) = \frac{x + 1}{5 \;-\; 2x}. (x \neq \frac{5}{2}$ and $x \neq \frac{-1}{2})$.

Here, $y = \frac{x + 1}{5 \;-\; 2x}$ … $x\neq \frac{5}{2}$

Interchange x and y.

$x = \frac{y + 1}{5 \;-\; 2y}$

$5x\;-\;2xy = y + 1$

$5x\;-\;1 = 2xy + y$

$5x\;-\;1 = y(2x + 1)$

$y = \frac{5x \;-\; 1}{2x + 1}$

$f^{-1}(x) = \frac{5x \;-\; 1}{2x + 1}$ … $x \neq \frac{-1}{2}$

How to Find Inverse Functions Using Algebra

We can replace f(x) with y and solve the algebraic expression in terms of x. 

Consider an example.

Function: $f(x) = 5x \;-\; 9$

Replace the f(x) with y: $y = 5x \;-\; 9$

Add 9 to both sides: $y + 9 = 5x$

Divide both sides of the equation by 5: $\frac{y + 9}{5} = x$

Exchange the sides: $x = \frac{y + 9}{5}$

Solve the expression replacing x with $f^{-1}(y) = \frac{y + 9}{5}$

Facts about Inverse Function

Conclusion

In this article, we learnt about Inverse functions, their graphs, and steps for finding inverse functions. Let’s solve a few solved examples and practice problems.

Solved Examples On Inverse Function

1. What is the inverse of the function $f(x) = x + 1$?

Solution: 

Given function: $f(x) = x + 1$

Replace f(x) by y. 

$y = x + 1$

Interchange x and y.

 $x = y + 1$

Solve for y.

$y = x\;-\;1$

Replace y by $f^{-1}(x)$.

$f^{-1}(x) = x\;-\;1$

2. Find the inverse of $f(x) = x$?

Solution: 

Given function: $f(x) = x$

Replace f(x) by y.

$y = x$

Interchange x and y.

$x = y$

Solve for y.

$y = x$

Replace y by $f^{-1}(x)$.

$f^{-1}(x) = x$

The inverse of an identity function is the identity function itself.

3. What is the inverse of a function $g(x) = 5(x + 3)$?

Solution: 

$g(x) = 5(x + 3)$

$y = 5(x + 3)$

$x = 5(y + 3)$

$x = 5y + 15$

$y = \frac{x \;-\; 15}{5}$

$g\;-\;1(x) = \frac{x \;-\; 15}{5}$

4. If $g(x) = 8\;-\;\frac{x}{3}$, and  $f(x) = 24\;-\;3x$ , show that f and g are inverses.

Solution:

i) $g(x) = 8\;-\;\frac{x}{3}$

$f(g(x)) = f(8\;-\;\frac{x}{3})$

$f(g(x)) = 24\;-\;3(8\;-\;\frac{x}{3})$

$f(g(x))= 24\;-\;24 + x$

$f(g(x)) = x$

ii) $f(x) = 24\;-\;3x$

$g(f(x)) = g(24\;-\;3x)$

$g(f(x)) = 8\;-\;\frac{(24\;-\;3x)}{3}$

$g(f(x)) = 8\;-\;8 + x$

$g(f(x)) = x$

From (i) and (ii), we have $f(g(x)) = x = g(f(x))$

Thus, f and g are inverses.

Practice Problems On Inverse Function

Frequently Asked Questions On Inverse Function