- What Is Multiplication on a Number Line?
- How to Represent Multiplication on a Number Line
- Understanding the Properties of Multiplication on a Number Line
- Solved Examples on Multiplication on a Number Line
- Practice Problems on Multiplication on a Number Line
- Frequently Asked Questions about Multiplication on a Number Line
What Is Multiplication on a Number Line?
Multiplication on a number line refers to finding the product of two numbers with the help of a number line.
Multiplication is defined as repeated addition. It is a fundamental arithmetic operation in mathematics.
The concept of equal groups is closely connected to multiplication. In multiplication, you combine equal groups of objects to find the total quantity.
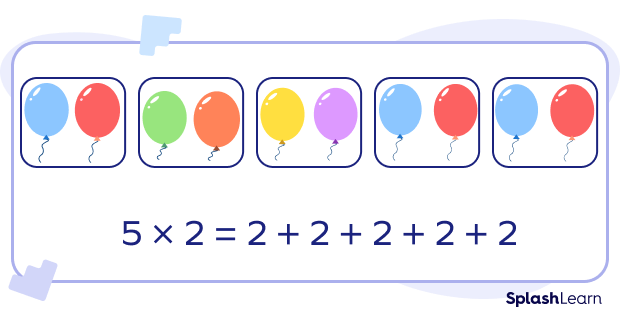
Example: 5 × 2 simply means “5 equal groups of 2.”
We can write as a repeated addition.
5 × 2= 2 + 2 + 2 + 2 + 2
Check out 5 groups of balloons, where each group has 2 balloons each.
Using a number line for a multiplication is the best way to visualize different multiplication facts. A number line is a straight line used to visually represent numbers in a particular range.
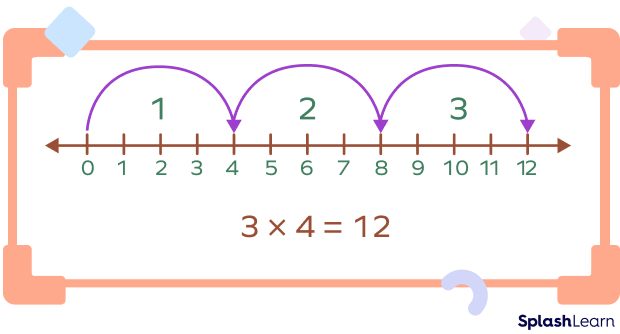
How to show multiplication on a number line? Let’s see. Suppose we want to multiply the number 3 by the number 4.
3 × 4 = 3 groups of 4 = 3 jumps of 4
Starting from zero, we take 3 jumps such that each jump has four steps. This is also known as “skip counting.”
In other words, form three groups of 4 equal intervals starting from 0. The last number that we land on is our answer.
Recommended Games
How to Do Multiplication on a Number Line
We consider two cases when multiplying numbers on a number line.
Case 1: Multiplying two positive numbers
Here, we form equal groups of intervals starting from 0 and to the right of 0 (on a positive number line).
Case 2: Multiplying a positive number and a negative number
Here, we form equal groups of intervals starting from 0 and to the left of 0 (on a negative number line).
Let’s note some important points.
| (+) × (+) = (+) | The product of two positive numbers is always positive. |
| (-) × (-) = (+) | The product of two negative numbers is always positive. |
| (-) × (+) = (-) | The product of a positive number and a negative number is negative. |
| Even-Odd Rule:If we multiply even number of negative numbers, the product is positive.If we multiply odd number of negative numbers, the product is positive. | |
When we multiply a number by (-1), we get its additive inverse. 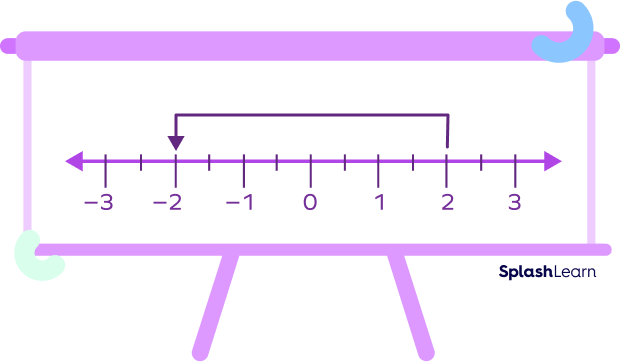 | |
Recommended Worksheets
How to Represent Multiplication on a Number Line
On a number line, the position of zero is exactly in the middle of the number line. To the right of the zero, there are positive numbers. To the left of the zero, there are negative numbers.
- Multiplication of Positive Numbers on a Number Line
Consider an example.
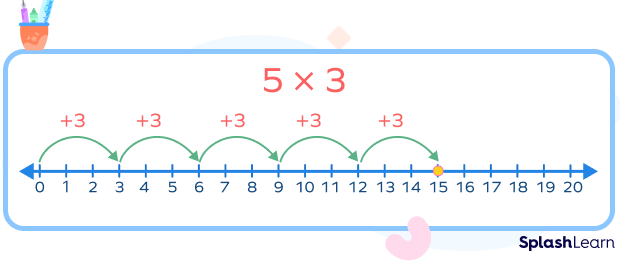
Example: 5 × 3
5 × 3 = 3 + 3 + 3 + 3 + 3
We take 5 jumps of 3 starting from 0 to the right.
- Multiplication of a Positive Number and a Negative Number on a Number Line
What happens when we multiply a negative number with a positive number on a number line? Let’s understand with the help of an example.
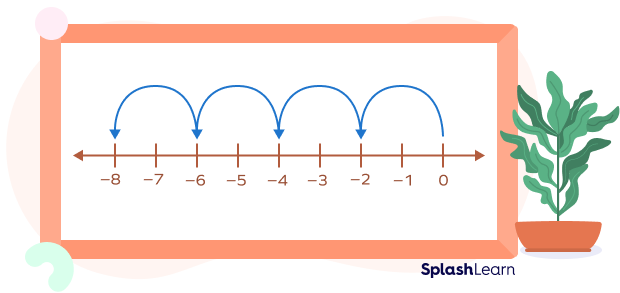
Example: 4 × (–2)
4 × (-2) = (-2) + (-2) + (-2) + (-2)
Take 4 jumps of 2 to the left of 0.
Understanding the Properties of Multiplication on a Number Line
Number line multiplication is also useful to understand different properties of multiplication, such as the commutative property, the associative property, and the distributive property.
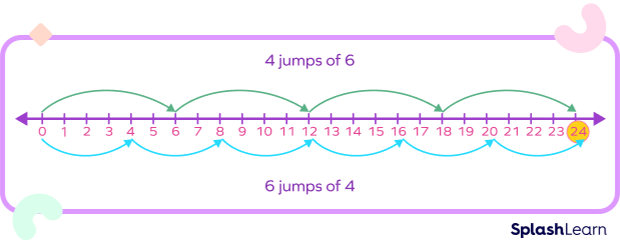
Consider an example. The commutative property of multiplication states that the order in which we multiply two numbers does not affect the result.
This property can be visualized on the number line by observing that the distance between two points on the number line is the same regardless of which point we start from.
Example: 6 × 4 = 4 × 6 = 24
Solved Examples on Multiplication on a Number Line
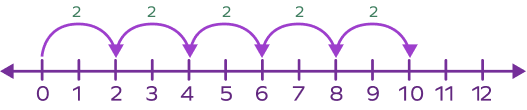
1. Multiply 2 and 3 on the number line.
Solution:
2 × 3 = 3 + 3 = 2 jumps of 3 starting from 0 (to the right)
Starting from zero, 2 groups of 3 equal intervals need to be formed on the number line.
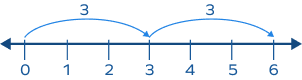
We landed on 6. The product is positive since both numbers are positive.
Thus, 2 × 3 = 6
2. What is the product of (–6) and 3 on the number line?
Solution:
(–6) × 3 = 6 jumps of 3 to the left of 0
We move to the left due to the negative sign associated with 6.
Starting from zero, 6 groups of 3 equal intervals need to be formed on the number line. Since one is a positive integer and the other is negative, the product will be negative.
We land on (–18).

3. Multiply 4 and (–5) on a number line.
Solution:
(4) × (–5) = (–5) + (–5) + (–5) + (–5) = 4 jumps of 5 to the left 0
We move to the left due to the negative sign associated with 5.
Starting from zero, 4 groups of 5 equal intervals need to be formed on the number line. Since one is a positive integer and the other is negative, the product will be negative. We land on –20.

4. Identify the multiplication operation that the given number line represents.

Solution:
We can see 3 groups or 3 jumps starting from 0.
Each group or interval has 5 equal parts.
Starting from zero, 3 groups of 5 equal intervals are formed.
Since both are positive integers, the product is to the right of 0.
The final number we landed on is 15.
Thus, the number line represents the multiplication 3 × 5 = 15.
5. Using the number line, multiply 4 and 6.
Solution:
Starting from zero, 4 groups of 6 equal intervals need to be formed on the number line. This way we will reach 24 forming 4 individual groups. Since both are positive integers, the product will be to the right of 0.

Practice Problems on Multiplication on a Number Line
Multiplication on a Number Line – Definition with Examples
Choose the multiplication fact shown on the number line.

There are 3 groups of 5.
So, the multiplication fact is 3 ✕ 5.
Which of the following number lines represent the multiplication of (-2) and 8?
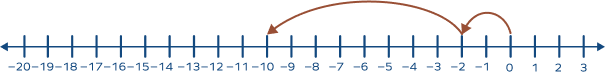
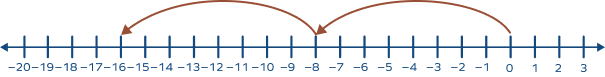
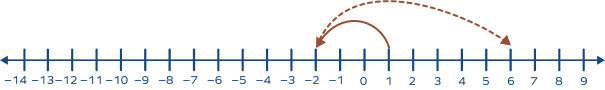

We need to find 2 groups of 8, starting from 0, to the left of 0.
This way we will reach – 16.
Which multiplication fact is shown by the following number line?
5 jumps of 2 = 5 ✕ 2
The multiplication fact shown by the number line given below is:

Starting from zero, 4 groups of 2 equal intervals need to be formed on the number line. This way we will reach – 8 forming 4 individual groups. Since both are positive integers, the product will be to the left of 0.
Find the multiplication fact shown on the number line given below.

4 ✕ 5 = 4 groups of 5 equal intervals on the right of 0
Frequently Asked Questions about Multiplication on a Number Line
How does the division on the number line work?
Division is known as repeated subtraction. Starting from the dividend, we take the jumps of the length equal to the divisor until we reach 0. The number of jumps we take represents the quotient.
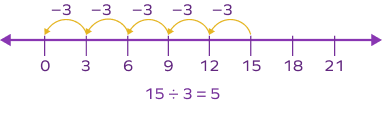
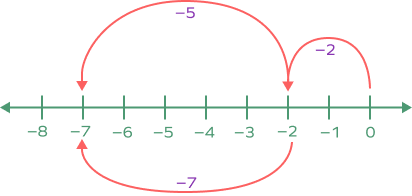
How do you add two negative integers on the number line?
Suppose we have to add (-a)+(-b). First mark the first number “-a” on the number line. Then, we move towards the left from the marked number by “b” units.
(-5)+(-2) = (-7)
How do you subtract two positive numbers on the number line?
To find a-b, we first mark the number a on the number line and then move b units to the left.
What is skip counting? How can you use the number line to skip count?
To skip count means to count by skipping through a particular number of places in the counting sequence. On a number line, we take jumps of equal size each time. Take note of the numbers.
What are manipulatives used for teaching multiplication to kids?
Manipulatives used for teaching multiplication to kids include items like counters, number lines, arrays, tiles, or blocks.




































