Number Bond: Introduction
Number bonds show the bond between two numbers and their sum.
It visually demonstrates the relationship between the parts (the numbers) and the whole (the sum).

Recommended Games
What Are Number Bonds?
A number bond is a pair of numbers that add up to give the sum as a specific number. Using number bonds, one can instantly tell the answer without the need for the actual calculation.
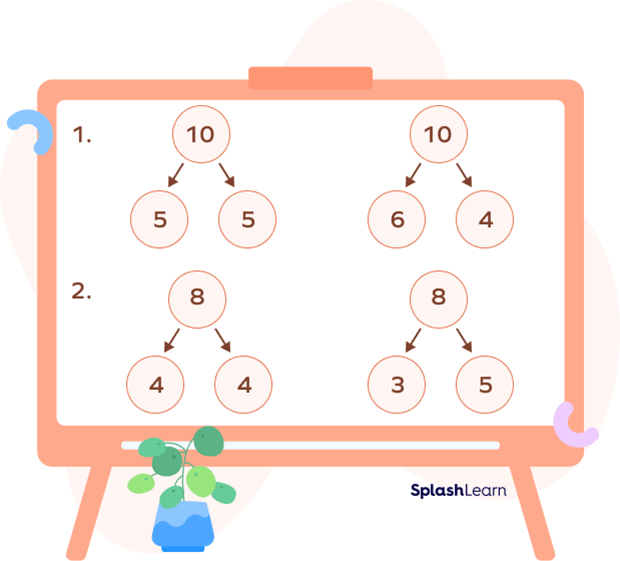
In the example above, when we see a number bond, we instantly know the answer without having to calculate it. They help us understand that a whole number is made up of parts and that these parts could be in different proportions.
Let’s understand this concept more clearly with the help of some number bond examples.
Recommended Worksheets
Number Bonds of 5
In this number bond, 5 is a whole number made up of combinations of different parts, as shown in the image below.

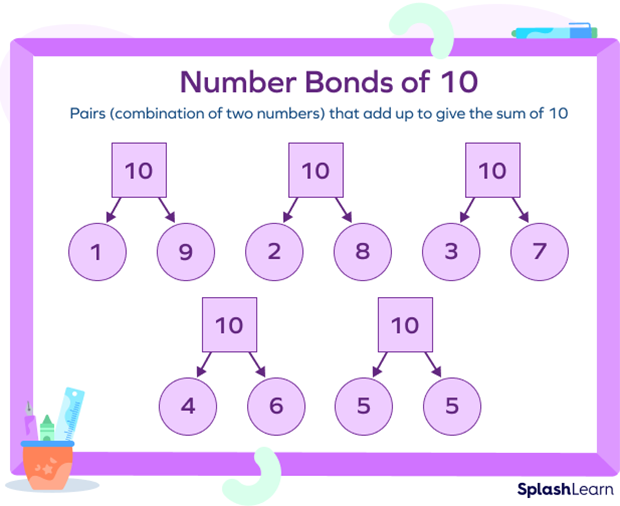
Number Bonds of 10
In this number bond, 10 is a whole number made up of combinations of different parts, as shown in the image below.
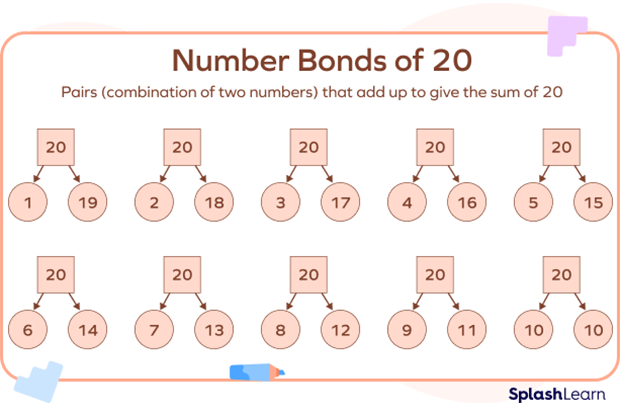
Number Bonds of 20
In this number bond, 20 is a whole number made up of combinations of different parts, as shown in the image below.
Number Bonds: Addition
Number bonds are very useful while learning addition in basic arithmetic.
For example:

In the example above, we break number 7 into two parts. The value of the first part is 2, and the value of the second part is 5.
While we are familiar with $5 + 5 = 10$, it becomes easier to find that $10 + 2 = 12$.
Number bonds are helpful when we need to add many different numbers. In such cases, grouping similar numbers helps make addition easy.
For example: $2 + 7 + 4 + 6 + 8 + 3 =$ ?
In this case, if we know the number bonds for 10, we can easily combine the numbers that give us 10 and make our calculations simpler and faster.
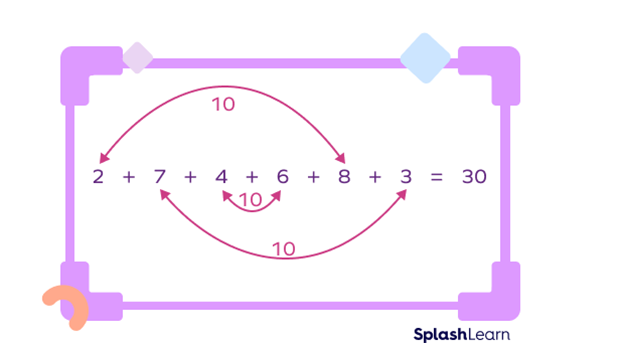
So here, we have $2 + 8 = 10, 7 + 3 = 10$, and $4 + 6 = 10$.
So, we get the sum as $10 + 10 + 10 = 30$.
Number Bonds: Subtraction
Number bonds are very useful while learning subtraction in basic arithmetic.
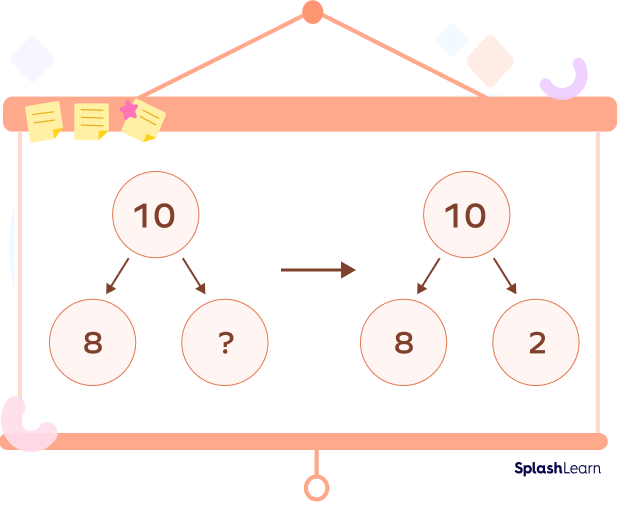
For example: $10 − \underline{} = 8$
Here, we know that 10 is the whole number, and 8 is one of the numbers from the pair of number bonds. The other number that combines with 8 to give us 10 is 2.
So, $10 − 2 = 8$.
Fun Fact!
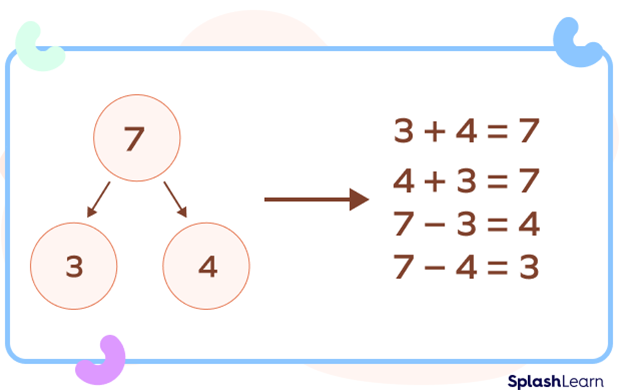
- If we know the 3 numbers of a number bond, we can make 2 addition and 2 subtraction sentences with those 3 numbers.
For example:
Number Bonds: Division
Number bonds are also very useful while learning division in basic arithmetic.
For example, if we have to determine $10/5 =$ ?
Here, 10 is a whole number. 5 is one part of a pair that makes up 10. To find the other part of the pair, we need to know multiplication, i.e., 5, when multiplied by 2, makes 10.
$5 \times 2 = 10$
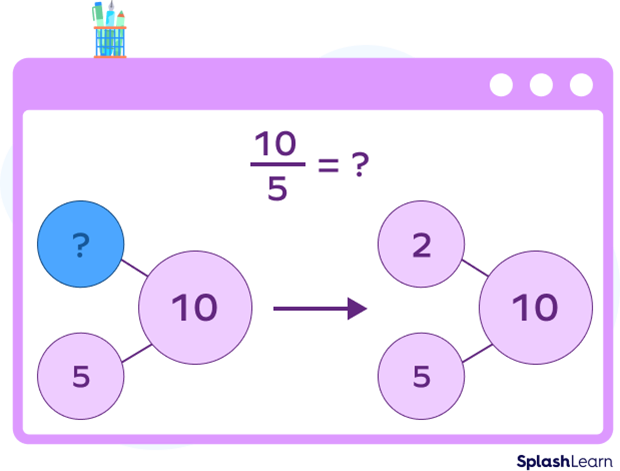
Since multiplication and division share an inverse relationship, 2 will be the other part of the pair.
So, $10/5 = 2$.
Benefits of Number Bonds
Understanding and learning the concept of number bonds has the following benefits:
- Makes it easier to use inverse operations
- Assists with basic mental arithmetic
- Simple to remember and highly effective
- Boost creativity and problem-solving skills
How Can You Teach Number Bonds to Children?
Now that you know the number bond definition and its benefits, let’s delve further into how you can teach kids this concept.
The best approach to teaching number bonds in first grade is the CPA (Concrete-Pictorial-Abstract) approach, which consists of the following three steps:
Concrete Step
In this step, you can ask the children to begin counting recognizable, interactive real-world objects. Then, ask them to represent actual objects with counters, followed by sorting the counters into two groups.
With this, children can discover the various ways of forming number bonds after dividing the counters into two groups.
For example, 6 can be made by the sum of the pairs of 4,2; 3,3; 5,1; 0,6, as shown in the image below:

Pictorial Step
In this step, once children have grasped the concept of number bonds through physical objects, you can teach them to write number bonds in workbooks or on whiteboards.
You can also teach them how to represent number bonds with the help of pictures and illustrations, as shown in the image below.

Abstract Step
Once the children have mastered the concrete and pictorial steps, you can teach them how to represent and solve abstract problems with the help of mathematical notations.
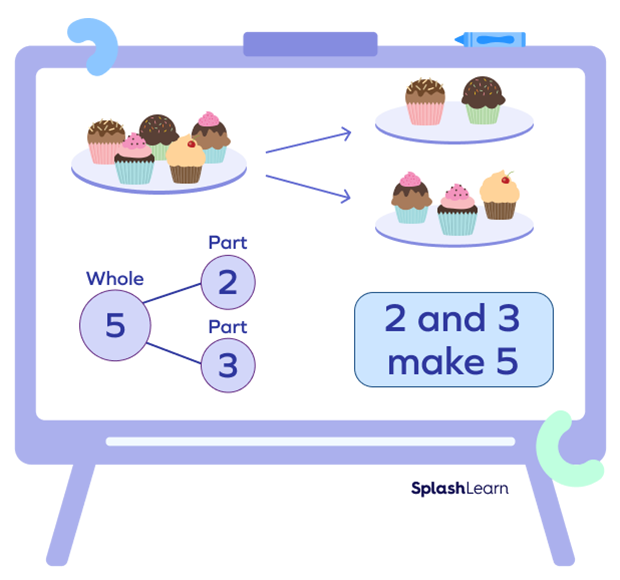
For example, a pictorial representation of 5, as shown below, will have the mathematical notation as $2 + 3 = 5$.
Conclusion
A number bond in math refers to a combination of pairs, which, when added, give the sum as a whole number. It helps in learning how to perform basic arithmetic operations like addition, subtraction, division, etc., easily.
Since number bonds lay the foundation for understanding complex math, it is crucial to teach them only with highly effective approaches like the CPA approach. It helps children gain mastery over the concept and also enhances their creativity and problem-solving skills.
Solved Examples on Number Bonds
1. Find $13 + \underline{} = 21$.
Solution: The number bonds for the whole number 21 consist of the following combination of pairs:
1,20; 2,19; 3,18; 4,17; 5,16; 6,15; 7,14; 8,13; 9,12; 10,11.
From this, we know that 13 and 8 make 21.
So, $13 + 8 = 21$.
2. Determine $16 − \underline{} = 9$.
Solution: We know that 16 is a whole number. So, the combination of pairs that make up 16 are:
1,15; 2,14; 3,13; 4,12; 5,11; 6,10; 7,9; 8,8.
From this, we know that 7 and 9 are parts that make 16.
So, $16 − 7 = 9$.
3. Calculate $18\div3$.
Solution: Here, 18 is a whole number, and 3 is one part of the pair. To find the other part, we need to use multiplication.

So, when 3 and 6 are multiplied, the product is 18.
Since division and multiplication are inversely related, the final answer will be 6.
$18/3 = 6$.
$4. 2 + 5 + 10 + 15 + 18 + 10 = $?
Solution: The numbers can be grouped into three pairs to make 20. Since we already know the number bonds for 20, we can easily find the answer.
Here, $2 + 18 = 20 − (i)$
$5 + 15 = 20 − (ii)$
$10 + 10 = 20 − (iii)$
Upon adding (i), (ii), and (iii), we will get
$20 + 20 + 20 = 60$.
5. Complete the number bond.
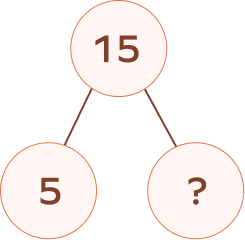
Solution: Here, 15 is a whole number, and 5 is one part of the pair that makes up 15.
To complete the bond, we need to find the other part of the pair.
For that, we need to know the combination of pairs that make up 15, which are:
1,14; 2,13; 3,12; 4,11; 5,10; 6,9; 7,8.
From this, it is clear that 5 and 10 make up 15. So, to complete the number bond, 10 will be the other part of the pair.
Practice Problems on Number Bonds
Number Bonds – Definition with Examples
Find $21 + \underline{} = 30$.
30 is a whole number that can be made up of several combinations of pairs, including 21 and 9.
This means that 9 and 21 are parts of a pair, which, when added, make 30 as their sum.
Find the correct option.
Since 32 is a whole number, several combinations of pairs make up 32, including 26 and 6.
Determine $19 – 4 =$ ?
19 is a whole number that can be made from several combinations of pairs, including 15 and 4.
This means that 15 and 4 are parts of a pair. When we subtract 4 from 19, we will get 15 as the answer, the other part of the pair.
Complete the number bond.
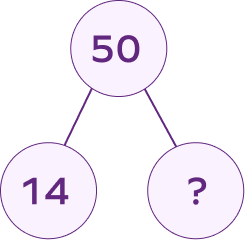
50 is a whole number that can be made from numerous combinations of pairs, including 14 and 36.
Find the incorrect option.
Since 22 is a whole number, several combinations of pairs or parts make 22, including 7,15; 10,12; 6,16; except 4,17.
Frequently Asked Questions on Number Bonds
What is another name for number bonds?
Number bonds are also known as number pairs.
Do we use number bonds to break a number into 2 parts only?
No, number bonds can be used to break down or split numbers into 2, 3 or more parts too. However, it is most convenient to split it into 2 or 3 parts.
Can number bonds be used with numbers different from whole numbers?
What is the need for number bonds?
Number bonds help to break down numbers in useful ways. They help students visualize and solve addition and subtraction problems easily.
What is the difference between number bonds and number facts?
Number bonds are one of many kinds of number facts. Number bonds can be addition number facts as two numbers are combined to form another one. Number facts, on the other hand, are not only for addition, but for subtraction, multiplication, and division too.




































