“Memorize the multiplication tables from 1 to 10. I shall ask questions tomorrow,” the math teacher announced. Anya was relieved because she already knew the multiplication tables.
She began writing them down in her notepad after brushing up on her tables. Suddenly, Anya noticed something unexpected. The multiples in the multiplication table generated a number series that followed a specific pattern.
For example, in the table of 2, its multiples 2, 4, 6, 8, 10 . . . form a number pattern where the next number is obtained by adding 2 to the preceding one. Anya discovered a similar sequence in the multiplication table for all numbers.

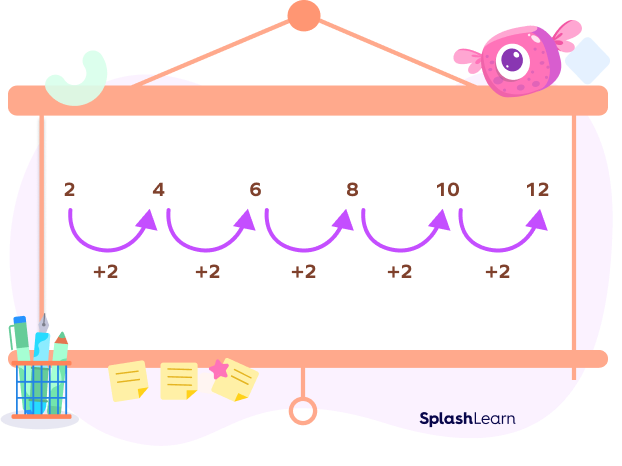
What is this wonder of numbers? What are number patterns? Let’s find out!
What Is a Number Pattern?
We’ve seen that the multiples of a number n exhibit a pattern where you’ll get the next number in the series by adding $n$ to the last number. Such a sequence found in a number series is a number pattern.
Number Patterns: Examples with Answers
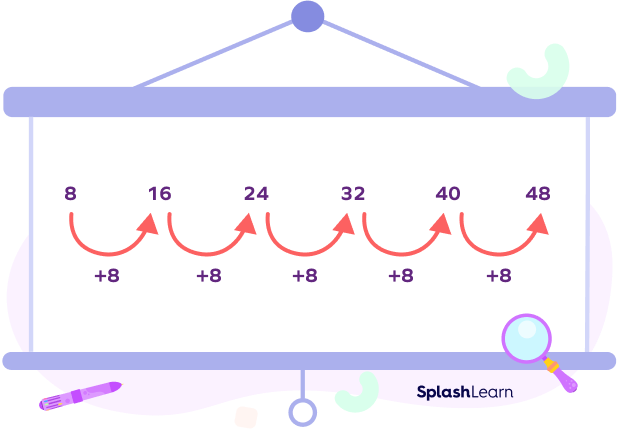
The common example for number patterns is multiplication tables. For instance, in the table of 8, we get the next number in the series by continuously adding 8 to the last number. So, we get a number sequence/pattern: 8, 16, 24, 32, 40, 48…
Example 1: Find the following number in the number patterns 7, 14, 21, 28, 35…
Solution: Multiples of 7 form the given sequence. Here, the difference between two consecutive numbers is 7. So, the next number will be $35 + 7 = 42$.
Counting and Number Patterns
We get multiples by counting numbers in a particular pattern. We’ll get multiples of n by counting in a pattern of n. Let’s understand it with an example.
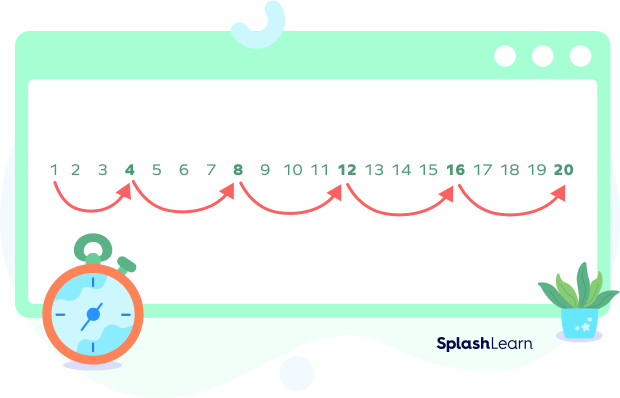
Example 2: Write the first five multiples of 4 by counting numbers in a pattern of 4.
Solution: By counting numbers in the pattern of 4, we get
4, 8, 12…16…20.
Recommended Games
Math Number Patterns Types
Arithmetic Number Patterns
Arithmetic number series is the most common number pattern. Here, we get the following number in the sequence by adding/subtracting a constant to/from the previous number.
This constant, or the difference between two consecutive numbers in an arithmetic number pattern, is a common difference.
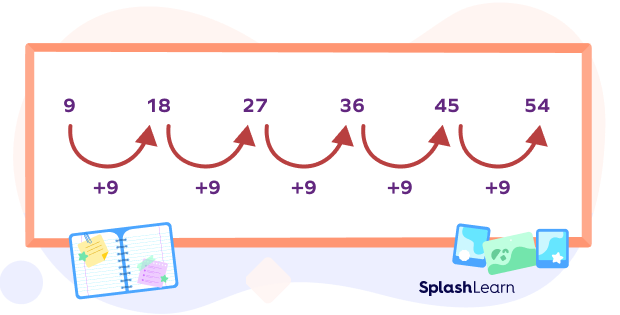
All multiplication tables are arithmetic number patterns. For instance, in the sequences 9, 18, 27, 36, 45, 54 … the common difference is 9. We get the following number by continuously adding 9 to the last number.
Geometric Number Patterns
In geometric number patterns, we get the next number in the series by multiplying or dividing a constant to/from the previous number. This constant, or the ratio of two consecutive numbers, is called the common ratio.
An example of a geometric number pattern is 3, 6, 12, 24, 48, 96… Here, the common ratio is 2, and we get the following number in the sequence by continuously multiplying two by the last number.

Square Number Pattern
A square number pattern is a series of square numbers. When we multiply a number by itself, we get the square of that number. Square numbers are, therefore, squares of any number.
An example of a square number pattern is 1, 4, 9, 16, 25, 36… Here, the squares of consecutive numbers from 1 to 6 form the number pattern.
Cube Number Pattern
Similar to a square number pattern, a cube number pattern is a series of cubes. We get cubes when we multiply a number by itself thrice.
An example of a cube number pattern is 1, 8, 27, 64, 125, 216… Here, the cubes of consecutive numbers from 1 to 6 form the sequence.
Triangular Number Pattern
A triangular number pattern is a type of dot pattern where we create a number series representing the number of dots required to form equilateral triangles. Here, the sides of the triangles will have the same number of dots.
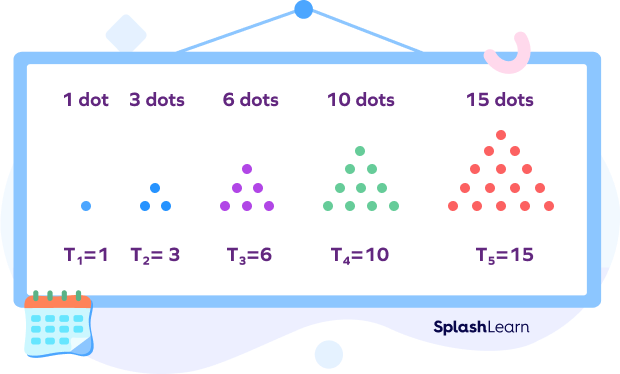
1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78… is a triangular number pattern. If we examine the pattern, we can say that the nth number in the triangular number pattern is the sum of all numbers from 1 to n. That is, the 6th number in the triangular pattern is the sum of all numbers from 1 to 6, i.e., $1 + 2 + 3 + 4 + 5 + 6$ or $21$.
Therefore, the formula for the nth number in a triangular series starting from 1 is $[n \times (n+1)] \div 2$. For instance, the 6th number in the pattern will be $[6 \times (6 + 1)] \div 2 = 21$.
Fibonacci Number Pattern
The Fibonacci number pattern is a series of Fibonacci numbers. Starting with 0 and 1, the next number in the Fibonacci series is the sum of the last two numbers.
The Fibonnaci series is 0, 1, 1, 2, 3, 5, 8, 13, 21, 34…
Here, (say) the 8th number, 13, is the sum of the 6th number 5 and 7th number 8. So, the nth number in the Fibonacci series is the sum of (n-2)th and (n-1)th number.
Recommended Worksheets
Number Patterns and Sequences Facts
The number of elements in a number pattern is endless. By applying the rule, you can continue the sequence endlessly.
A simple number pattern has only one rule. However, a complex number pattern has more than one rule. For instance, the pattern 3, 4, 6, 8, 9, 12, 12, and 16 … has two rules. The alternate numbers from 3 are multiples of 3, and the alternate numbers from 4 are the multiples of 4.
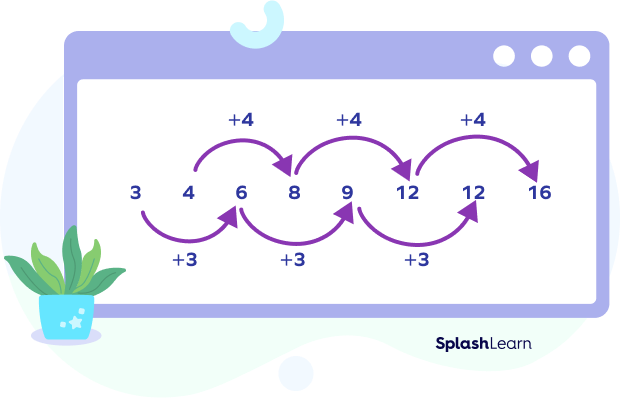
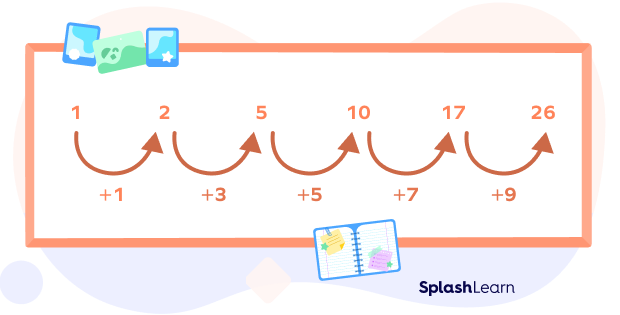
The rule of a number pattern can form a number pattern. For instance, if you subtract the consecutive terms in the pattern 1, 2, 5, 10, 17, 26, …, and make a series, we get 1, 3, 5, 7, 9, …
Solved Examples
1. What is the missing value in the sequences 5, 10, 15, __, 25, 30, …?
Solution: In the pattern, we get the next number by adding 5 to the previous number. So, the missing value is $15 + 5 = 20$.
2. What is the following number in the number pattern 3, 9, 27, 81, …?
Solution: In the pattern, the ratio of two consecutive numbers is 3. So, the following number is $81 \times 3 = 243$.
3. Consider the sequence 1, 3, 6, 10, 15, 21, 28… What is the 20th value in this number pattern?
Solution: This is a triangular number pattern. So, the 20th value is $[n \times (n+1)] \div 2$
$= [20 \times (20 + 1)] \div 2$
$= 210$
Practice Problems
Number Patterns - Definition With Example
The next number in the series 1, 8, 27, 64, 125, … is:
The series is a cube number pattern. So, the next number is $6\text{^}3 = 216$.
What is the next number in the series 1, 8, 9, 64, 25, 216, …
We can rewrite the series as $1\text{^}2, 2\text{^}3, 3\text{^}2, 4\text{^}3, 5\text{^}2, 6\text{^}3$, … So, the next number would be $7\text{^}2 = 49$.
What is the following number in the series 1, 3, 7, 15, 31, __ ?
The rule of the series is $2n+1$. So, we can rewrite it as $1, [(2 \times 1)+1], [(2 \times 3)+1], [(2 \times 7)+1], [(2 \times 15)+1]$… So, the next number would be $[(2 \times 31)+1] = 63$.
Frequently Asked Questions
Does the series of natural numbers form a number pattern?
Yes. Natural numbers 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, … form an arithmetic number pattern with common difference 1.
What is the common difference between the number patterns formed by the series of odd numbers and even numbers?
The series of even numbers and odd numbers are arithmetic number patterns with common differences 2.
How to find number patterns?
To find number patterns, you must identify the sequence’s rule(s) and its type. For instance, if the difference between two consecutive numbers of a series is the same, it is arithmetic.
What is a “rule” in number patterns?
All number patterns are a series of numbers following a specific rule. For instance, in the number patterns 6, 12, 18, 24, 30, …, the rule is $n + 6$.




































