Patterns – Definition With Examples

Definition

In math, a pattern is defined as a sequence of repeating objects, shapes or numbers. We can relate a pattern to any type of event or object. A pattern has a rule that tells us which objects belong to the pattern and which objects do not belong to the pattern. Let’s look at some examples of patterns:

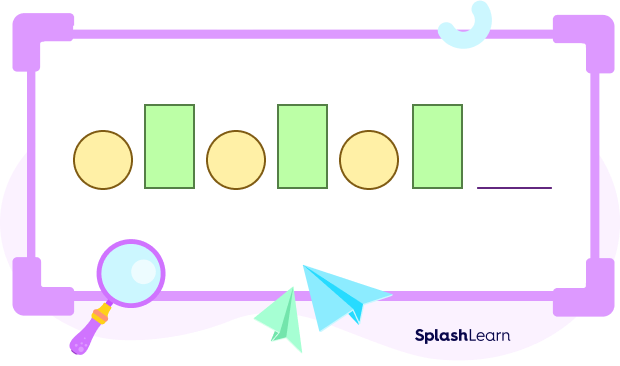
In the above image, the rule that is followed is that the circle is in the odd places and the rectangle is in the even places. So, the next figure in the pattern will be:  

Patterns exist all around us. We can find a pattern in the trees, in the window frames, on the floor, in our clothes, etc. One such real-life example is the zebra pattern. 

Patterns can be finite and infinite.

Finite Patterns

A finite pattern is a finite sequence in which we know the first term and the last term. 

For example: In the pattern 3, 6, 9, 12, 15, the first term is 3 and the last term is 15. 

Infinite Patterns

An infinite pattern is a sequence in which we know the first term but we don’t know the last term. 

For example: In the pattern 3, 6, 9, 12, 15, 18, ………; the first term is 3 but we don’t know where the pattern is going to stop.

Rules of Pattern

For creating a complete pattern, a certain set of rules need to be considered. For applying these rules, we should first understand the nature of the sequence and the difference between the two consecutive numbers given in the pattern. Some amount of guesswork is required and then we check to see whether the rule works throughout the whole pattern.

The patterns can be formed using three categories:

Repeating Pattern

The type of pattern in which the rule keeps repeating over and over is called a repeating pattern. It is generally common in letter and shape. 

Growing Pattern 

In a growing pattern, the numbers are placed in the increasing form or each number is greater than the previous number, then the pattern is known as a growing pattern. Example: 44, 50, 56, 62, …

Shrinking Pattern 

In a shirking pattern, the numbers are placed in the decreasing form or each number is smaller than the previous number. Example: 40, 35, 30, 25 … 

Types of Patterns

There are 3 types of pattern:

1. Shape Pattern 
2. Letter Pattern
3. Number Pattern

1. Shape Pattern

When a group of shapes are repeated, the pattern or sequence is known as a shape pattern. Shape patterns follow a certain sequence or order of shapes, i.e., they are repeated. The shapes can be simple shapes like circles, squares, rectangles, triangles, etc., or other objects such as arrows, flowers, moons, and stars.

For example: 

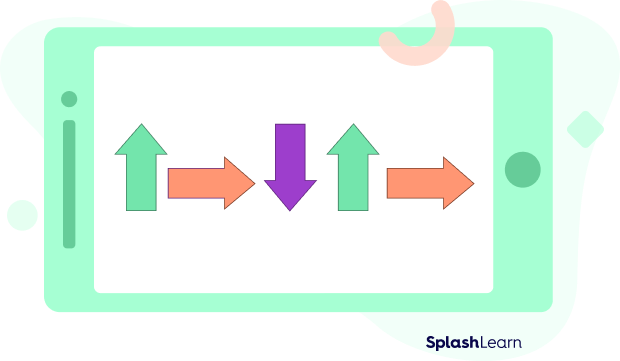
In the above pattern, the arrow is getting rotated at 90° and changes its color. Or, we can say that each colored shape is getting repeated after 2 shapes.

2. Letter Pattern

A sequence that consists of letters or English alphabets is known as a letter pattern. A letter pattern establishes a common relationship between all the letters.

For example: A, C, E, G, I, K, M… 

In the above pattern, one letter has been removed after every alphabet. 

3. Number Pattern

The most common type of pattern in mathematics is the number pattern, where a list of numbers follows a certain sequence based on a rule. 

There are different types of number patterns:

Arithmetic Pattern

Another name for arithmetic pattern is algebraic pattern. In such a pattern, the sequences are based on the addition or subtraction of the terms. If we know two or more terms in the sequence, then we can use addition or subtraction to find the arithmetic pattern.

Example 1: In the pattern 65, 64, 63, 62, 61, we are subtracting the consecutive numbers by 1 or each number gets decreased by 1. 

Example 2: In the pattern given below: 

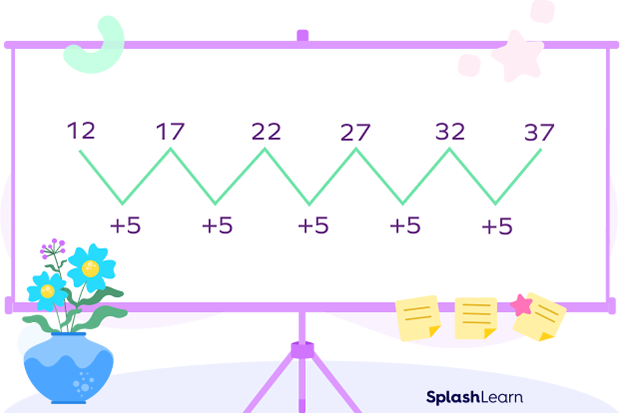
Each number is getting increased by 5. 

Geometric Pattern

A sequence of numbers that are based on multiplication and division is known as a geometric pattern. If we are given two or more numbers in the sequence, we can easily find the unknown numbers in the pattern using multiplication and division operations.

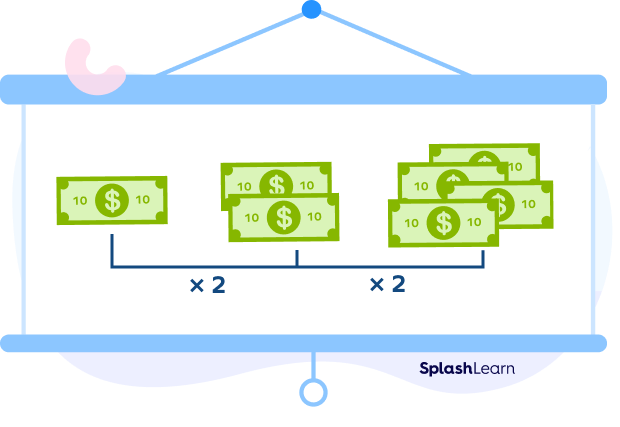
Example 1: Simran has $\$10$ as her savings in the first month. In the second month, her savings doubled. So, now she has 10 x 2= $\$$20. Again, in the third month her savings doubled. Now she has 20 x 2= $\$$40. So the pattern here is $\$$10, $\$$20, $\$$40.

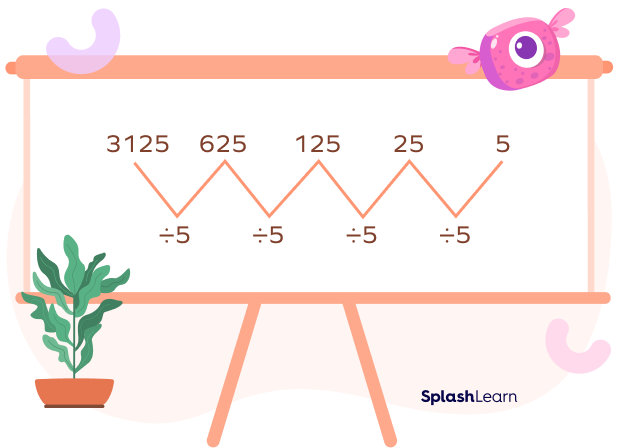
Example 2: In the pattern given below, each number is getting divided by 5. 

3125, 625, 125, 25, 5

Fibonacci Pattern

A sequence of numbers in which each number in the sequence is obtained by adding the two previous numbers together is known as the Fibonacci series or pattern. This sequence starts with 0 and 1. We add the two numbers to get the third number in the sequence.   

The sequence 0, 1, 1, 2, 3, 5, 8, 13 is the Fibonacci pattern. 

The pattern that is followed here is 0 + 1 = 1,  1 + 1 = 2 , 1 + 2 = 3 , 2 + 3 = 5, 3 + 5 = 8.

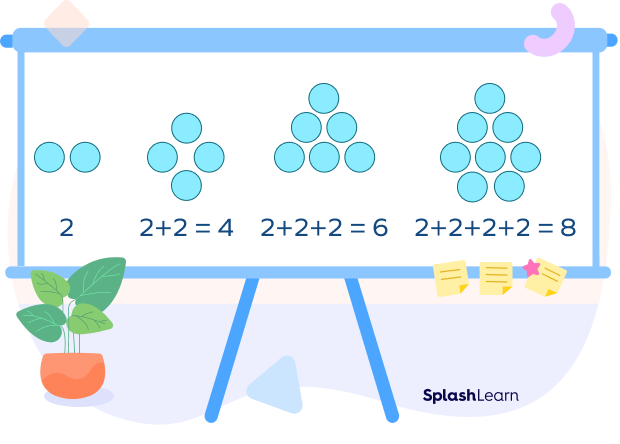
Triangular Number Pattern

The representation of the numbers in the form of an equilateral triangle arranged in a series or sequence is known as a triangular number pattern. The numbers in the triangular pattern are in a sequence of 1, 3, 6, 10, 15, 21, 28, 36, 45 and so on. 

The numbers in the triangular pattern are represented by dots. 

Example:

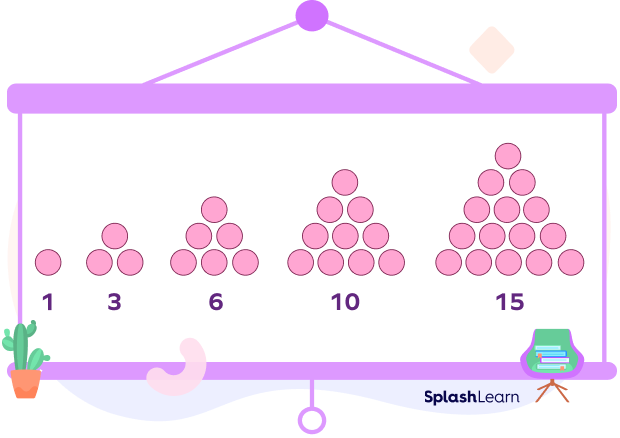
Also, the pattern can be described as 0 + 1 = 1, 1 + 2 = 3, 3 + 3 = 6, 6 + 4 = 10, 10 + 5 = 15 and so on.

Square Number Pattern

In the square number pattern, each number is a square of consecutive natural numbers. The pattern is written as:

$1^2,2^2,3^2,4^2,5^2$,…= 1, 4, 9, 16, 25…

Also, the pattern can be 1 + 3 = 4, 4 + 5 = 9, 9 + 7 = 16, 16 + 9 = 25 and so on. 

Basically, we add consecutive odd numbers in the sequence. 

Cube Number Pattern

In a cube number pattern, each number is the cube of consecutive natural numbers. The pattern is written as:

$1^3,2^3,3^3,4^3,5^3$…= 1, 8, 27, 64, 125…

The above number patterns are the ones that are commonly used. There are more number patterns. For example: odd number pattern, even number patterns, multiples pattern, etc.

Solved Examples

Example 1: What will be the next shape in the pattern? 

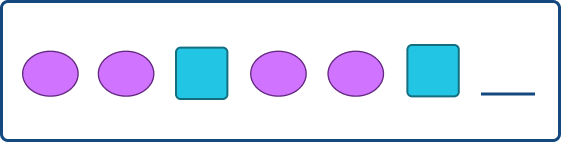
Solution: The pattern is 2 ovals and a square and the same pattern is being repeated. The next shape in the pattern will be an oval, i.e.: 

 

Example 2: Complete the pattern: 10, 13, 16, 19, ____, ____

Solution:

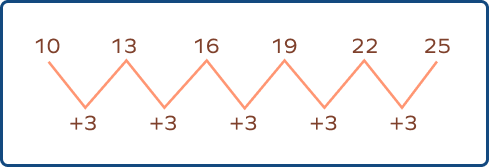
So, next numbers will be 19 + 3 = 22, 22 + 3 = 25

Example 3: Complete the pattern: AB, BC, CD, DE, ____, ____

Solution: The first term is the combination of first and second alphabets. The second term is the combination of second and third alphabets. The third term is the combination of third and fourth alphabets. The fourth term is the combination of fourth and fifth term. 

Similarly, the next two terms will be EF and FG.

Practice Problems

Frequently Asked Questions