- What Are the Lines of Symmetry in a Rhombus?
- Lines of Symmetry in a Non-Square Rhombus
- Lines of Symmetry in a Rhombus vs. Lines of Symmetry in a Square
- Solved Examples on Lines of Symmetry in a Rhombus
- Practice Problems on Lines of Symmetry in a Rhombus
- Frequently Asked Questions about Lines of Symmetry in a Rhombus
What Are the Lines of Symmetry in a Rhombus?
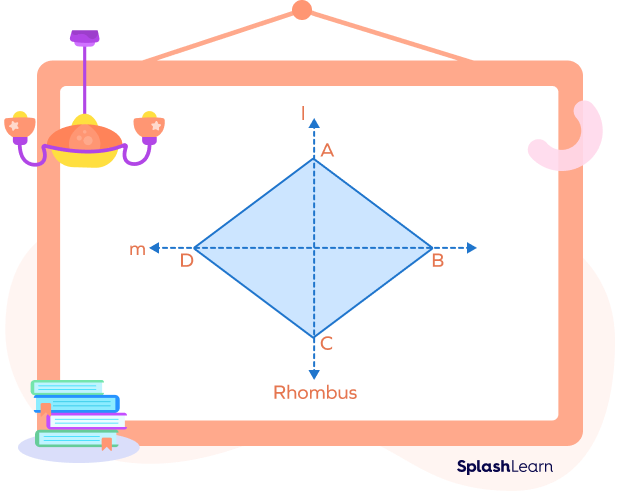
A rhombus is a quadrilateral that has 2 lines of symmetry. The lines of symmetry in a rhombus are the lines that divide it into two identical halves, each of which is the mirror image of the other.
A rhombus is a type of a parallelogram with four equal sides. Also, opposite angles of rhombus are equal. A rhombus is divided into two identical pieces by two lines of symmetry.
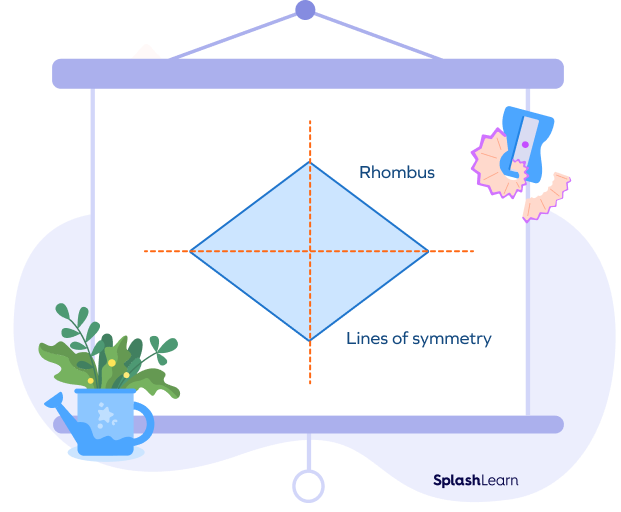
Diagonals of a rhombus coincide with its lines of symmetry. Therefore, it can be said that the two diagonals of a rhombus are its lines of symmetry.
Symmetry is the property by which we can divide a shape or an object into two identical halves. The lines of symmetry are the lines along which if we fold a symmetric object, its left and right parts would completely overlap with each other.
Recommended Games
How Many Lines of Symmetry Does a Rhombus Have?
A rhombus has two lines of symmetry. Diagonals of rhombus are where both of its lines of symmetry originate. Thus, it can be said the lines of symmetry in a rhombus are both its diagonals.
Lines of Symmetry in a Non-Square Rhombus
A square is a special type of a rhombus with each interior angle equal to 90. A non square rhombus is a rhombus whose sides are equal but the angles are not equal to 90.
Given below is a simple illustration of the shape of the square and non-square rhombus.
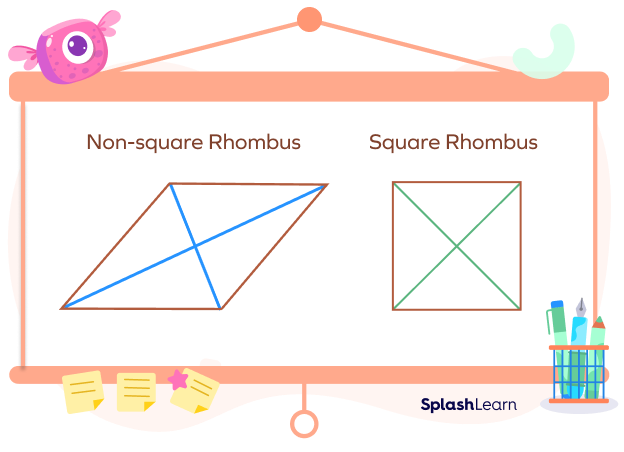
A non-square rhombus (or simply, a rhombus) has internal angles that are not equal to 90.
All angles of a square are equal to 90.
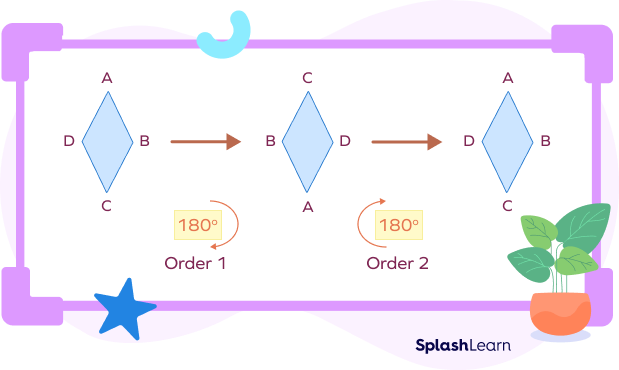
Rotational Symmetry in a Rhombus
A shape is said to possess rotational symmetry if it still looks the same after a rotation (rotation of less than 360 degrees). The number of positions in which the shape appears exactly the same as it did before the rotation is called the order of symmetry.
The order of rotational symmetry of a geometric object refers to how many rotations are required to make it appear identical to the original figure.
A rhombus has rotational symmetry of order 2 for the angle of rotation 180 degrees. Let’s rotate a rhombus by 90 degree, 180 degree, and 360 degree.
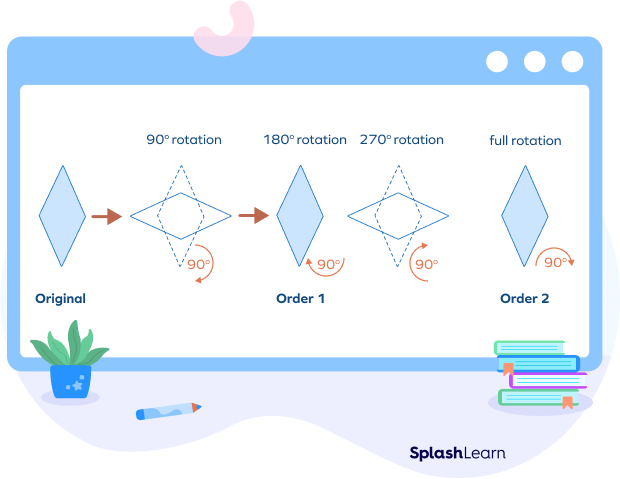
When you rotate it clockwise by 90 degrees or 270 degrees, you do not get the original shape. By 180 degree rotation & full rotation, you get the original rhombus shape.
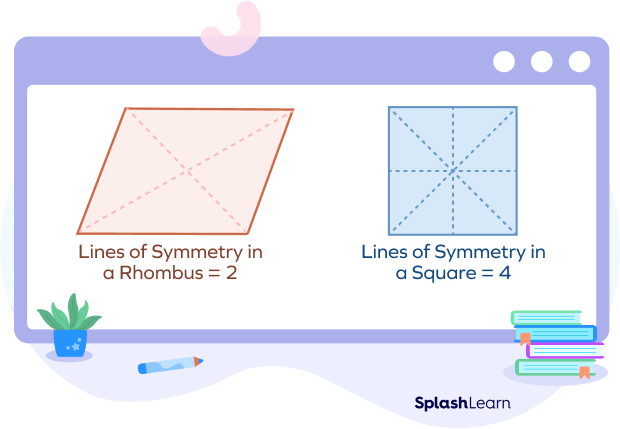
Lines of Symmetry in a Rhombus vs. Lines of Symmetry in a Square
We know that a rhombus is a two-dimensional geometric shape with equal sides. The angles of a rhombus are not 90 degrees, unlike those of a square. As a result, both the square and the rhombus have different numbers of lines of symmetry.
- Rhombus: A rhombus has 2 lines of symmetry. These lines pass through the opposite corners of the rhombus, bisecting each other at a right angle. Lines of symmetry in rhombus are drawn through its diagonals.
- Square: There are 4 lines of symmetry in a square. From these 4 lines of symmetry, two are drawn from these diagonals and two are drawn from its vertical and horizontal axis respectively.
Facts about Lines of Symmetry in a Rhombus
- Each of the two diagonals of a rhombus represents a line of symmetry.
- A circle has infinite lines of symmetry.
- The order of rotational symmetry of a square is 4.
Conclusion
In this article, we discussed lines of symmetry and rotational symmetry in a rhombus. Let’s solve some rhombus lines of symmetry examples and practice problems to understand the concept better.
Solved Examples on Lines of Symmetry in a Rhombus
Example 1: How many lines of symmetry does a rhombus have?
Solution:
If we fold the rhombus along the diagonal line, we get two identical halves. It is not possible if we fold the rhombus along its sides.
A rhombus has two lines of symmetry, which are basically its diagonals.
Example 2: Write whether the following statements are true or false .
a. A rhombus has rotational symmetry of order 1.
b. A rhombus has 4 lines of symmetry.
Solution:
a. A rhombus has rotational symmetry of order 1.
False.
Rhombus can rotate 360 degrees twice before it fits onto itself. As a result, we can say that a rhombus has rotational symmetry with order 2
b. A rhombus has 4 lines of symmetry.
False
A rhombus has 2 lines of symmetry which cuts it into two identical parts. Both the lines of symmetry in a rhombus are from its diagonals. So, it can be said the rhombus lines of symmetry are its both diagonals.
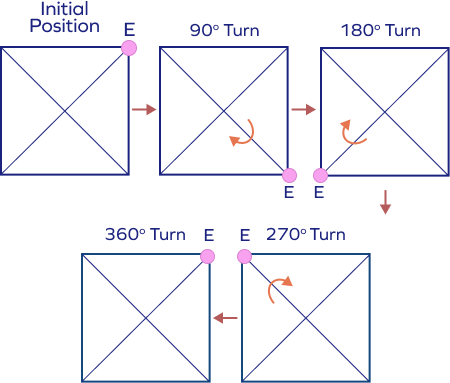
3. What is the order of rotational symmetry in a square?
Solution:
As we can see in the figure, the square matches itself 4 times during a full rotation of 360º. Hence, it has the rotational symmetry of order 4.
Practice Problems on Lines of Symmetry in a Rhombus
Lines of Symmetry in a Rhombus - Definition, Facts, Examples
How many lines of symmetry are there in a rhombus?
There are two lines of symmetry in a rhombus which cuts it into two identical parts.
What is the order of rotational symmetry for a rhombus?
A rhombus when rotated comes back to its original shape twice, once at 180 degree rotation and then at full rotation.
The number of times a figure fits into itself in one complete rotation is called the order of __________ symmetry.
The number of times a figure fits into itself in one complete rotation is called the order of rotational symmetry. A figure has a rotational symmetry of order 1, if it can come to its original position after full rotation or 360º.
What is the order of rotational symmetry in a square?
The order of rotational symmetry in a square is 4.
The lines of symmetry in the rhombus are its __________.
Diagonals of rhombus are where both of its lines of symmetry originate.
Frequently Asked Questions about Lines of Symmetry in a Rhombus
What does it mean when the order of rotational symmetry is 1?
Any object will come back to its original position after a full rotation. So, every object has a rotational symmetry of order 1. To be specific, shapes with no symmetry have rotational symmetry order 1.
Does a rhombus have rotational symmetry?
Yes, a rhombus has rotational symmetry of order 2 with angle of rotation 180°.
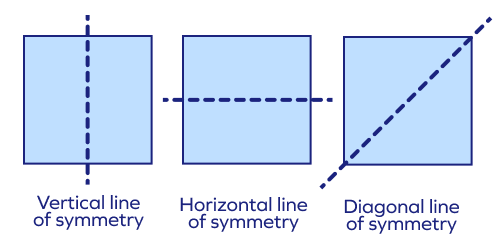
What are the various lines of symmetry ?
- Vertical lines of symmetry
- Horizontal lines of symmetry
- Diagonal lines of symmetry
Which shape is an example of no rotational symmetry?
A kite is an example of no rotational symmetry. A shape with no rotational symmetry fits onto its original outline only once (after full rotation). Shapes with no rotational symmetry have rotational symmetry order 1.
How do you locate a shape’s line of symmetry?
To locate a shape’s line of symmetry, we can fold the shape in such a way that one half is similar to the other half. The line along which we have folded is known as the line of symmetry.
What is the angle of rotational symmetry ?
The angle of rotational symmetry is the smallest angle that a shape must be rotated to fit within its original outline. The angle of rotational symmetry can be found by dividing 360o by the order of rotational symmetry of the shape.
For example, a square has a rotational symmetry of order 4.
$360^{\circ} \div 4 = 90^{\circ}$ The angle of rotational symmetry of a square is 90o.
What is the smallest angle of rotational symmetry for a rhombus?
The smallest angle of rotational symmetry in a rhombus is 180o.


























