What Is a Right Circular Cone?
A right circular cone is a three-dimensional geometric shape characterized by a circular base and a single curved surface that extends to a point called the apex or vertex. Its axis (the line joining the vertex and the center of the circle at the base) is perpendicular to the plane of the base.
A cone can be of two categories, depending upon the position of the axis: Right circular cone and oblique cone. The axis of the cone is the line that joins the vertex to the midpoint of the circular base.
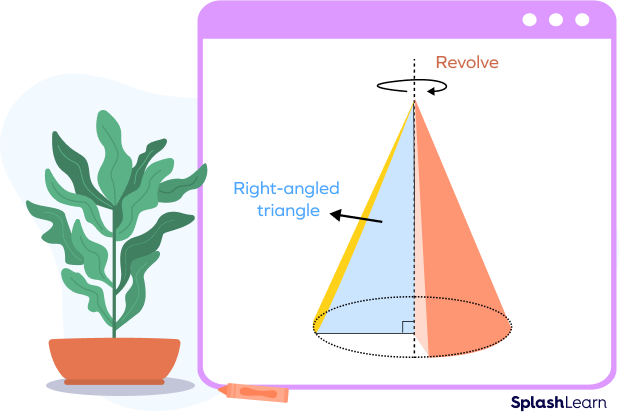
A right circular cone is one whose axis is perpendicular to the base. Here, the axis makes a right angle. A right circular cone is generated by a revolving right triangle about one of its legs.
In math, a cone is defined as a three-dimensional geometric figure with a flat base and curved surface pointed towards the top. The pointed end is the vertex, whereas the flat surface is called the base.
Recommended Games
Right Circular Cone: Definition
A right circular cone is a type of cone whose axis is perpendicular to the flat circular base.
Recommended Worksheets
What Are the Parts of a Right Circular Cone?
Let’s learn about the important parts or elements of a right circular cone.
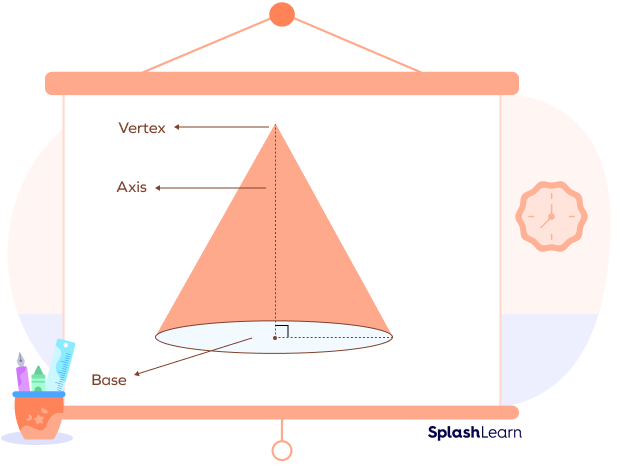
- Vertex of a Right Circular Cone: The flat circular base and the curved surface of a cone smoothly narrows down to a point called “vertex” or “apex.”
- Base of a Right Circular Cone: The base of a right circular cone is a circle.
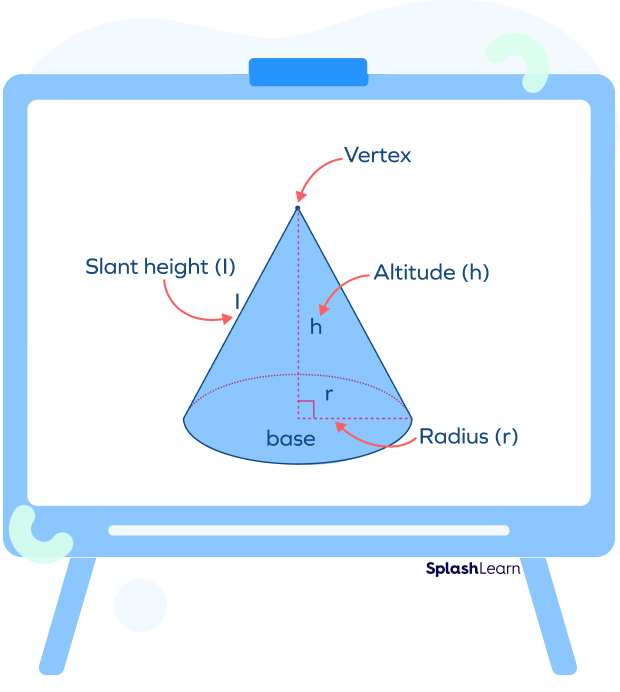
- Radius of a Right Circular Cone: It is the radius of the circle at its base.
- Axis/Height of a Right Circular Cone: The fixed line which joins the vertex and center of the base is called the axis/height of the cone.
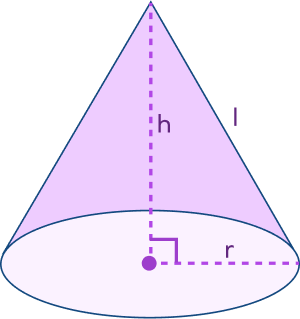
- Slant Height of a Right Circular Cone: The length of the line joining the vertex to any point on the circular edge of the base is called slant height. Generally, It is denoted by “l.”
Properties of Right Circular Cone
- It has one circular base.
- It has one vertex (apex).
- It has one curved edge.
- Slant height of the right circular cone is the line joining the vertex to any point on the circular edge of the base.
- A right circular cone is created by rotating a right triangle with the perpendicular side as the axis of rotation.
Right Circular Cone Formulas
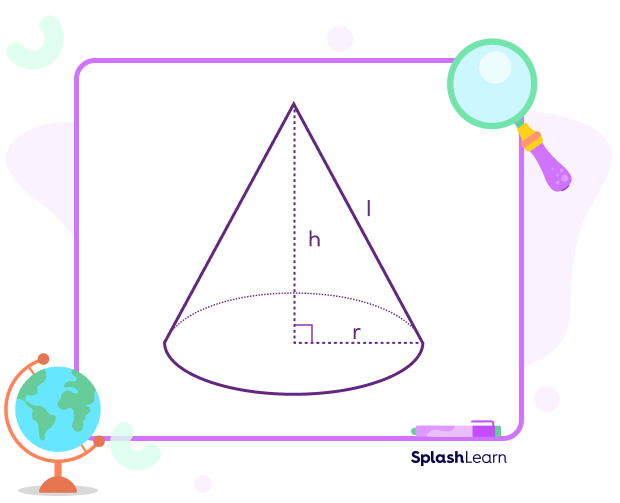
Consider a right circular cone with radius “r,” height “h,” and slant height “l.”
- Relationship between slant height, height, and radius: l2 = h2 + r2
- Curved surface area of right circular cone = π r l
- Total surface area of a right circular cone = πr(r + l)
- Volume of a right circular cone $= \frac{1}{3} \pi r^{2} h$
Surface Area of a Right Circular Cone
The surface area of a three-dimensional shape is the sum of all of the surface areas of each of the sides. A right circular cone has two surface areas:
- Lateral surface area/Curved surface area
The lateral surface area/curved surface area is the surface of the cone excluding the flat circular base.
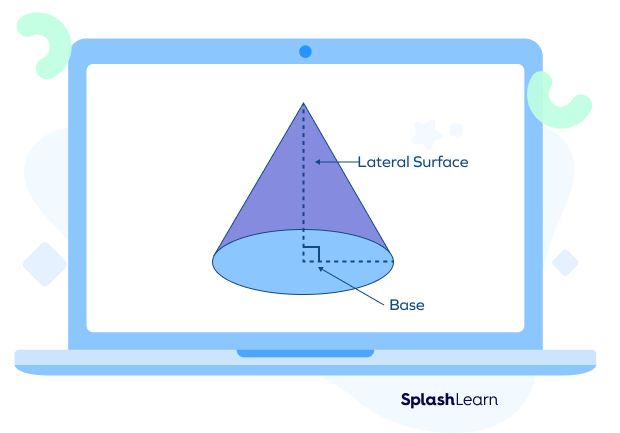
Here, “h” is the height, “l” is the slant height, “c” is the circumference of the base, and ”r” is the radius of the base. If we unroll it, the shape is as follows:
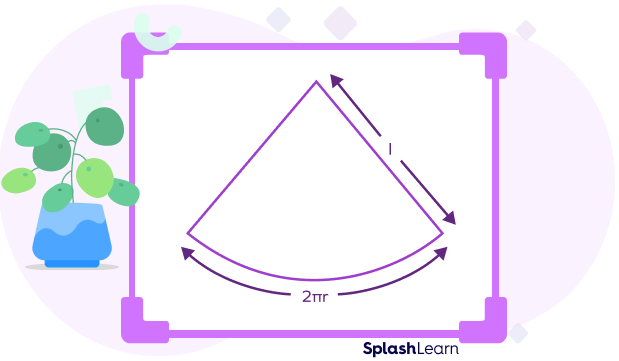
It is a sector of a circle with a radius ”l” and arc length “c.” So, the curved surface area of the cone is equal to the area of the above sector having radius l. The area of a sector given the arc length ”c” and radius “l” is given by,
∴ Curved surface area = Area of sector $= \frac{1}{2} \times 2\pi rl = \pi rl$
- Total Surface Area of a Right Circular Cone
The lateral surface area plus the base area of the cone is equal to the total surface area.
Total surface area = Curved surface area + Area of circular base
= πrl + πr2
= πr(l + r )
∴ Total surface area =πr(l + r )
Volume of a Right Circular Cone
If a right circular cone has radius “r” and height “h,” then its volume is equal to the one-third of
the product of the area of the circular base and its height. Let’s understand how to find the volume of a right circular cone.
Volume of right circular cone formula:
Volume of a right circular cone $= \frac{1}{3} \times $(base area)$\times$ height $= \frac{1}{3} \pi r^{2} \times h$
Volume of a right circular cone $= \frac{1}{3} \times \pi r^{2} \times h = \frac{1}{3} \pi r^{2}h$
Volume is measured in cubic units.
Volume of a right circular cone using diameter: We know that $r = \frac{d}{2}$.
Volume of a right circular cone $= \frac{1}{12} \pi d^{2}h$
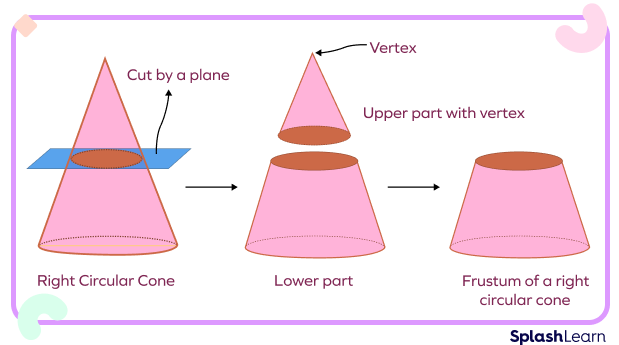
Frustum of a Right Circular Cone
When a right circular cone is cut off by a plane parallel to its base, a frustum forms in the area between the base and the parallel plane. And the upper part remains in the same shape as the right circular cone.
The lower part is called the frustum of a right circular cone.
Right Circular Cone vs. Oblique Cone
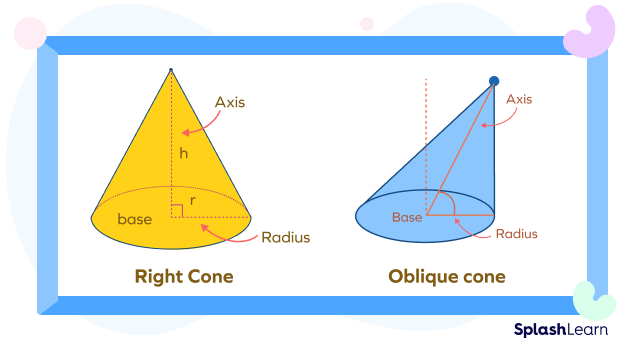
- A right circular cone or a regular cone has its axis perpendicular to its base. The axis joins the vertex to the center of the base.
- If the vertex position is not over the center of the base, it is an oblique cone. Here, the axis is non-perpendicular.
Real-life Examples of a Right Circular Cone
In our daily life, we come across many objects with conical shapes, such as an ice cream cone, a traffic cone, or a birthday hat.

Facts about Right Circular Cone
- The cone and pyramid are closely related geometric shapes, and interestingly, their surface area formulas share similarities.
- Right circular cones have rotational symmetry, which means they may be rotated around their axis while maintaining their appearance.
Conclusion
In this article, we learned about the right circular cone, its parts, properties, and formulas for finding the surface area and volume. We also learned about the frustum of a right circular cone, and some fun facts. Let’s solve a few examples and practice MCQs based on the learned concepts.
Solved Examples on Right Circular Cone
- Find the radius of a right circular cone whose slant height is 15 feet and height is 9 feet.
Solution:
l = 15 feet, and h = 9 feet.
Since, l2 = h2 + r2
152 = 92 + r2
225 = 81 + r2
r2 = 144
$r = \sqrt{144} = 12$
Hence, the radius of the given right circular cone is 12 feet.
- A cone has a circular base of radius 8 units and a height of 15 units.
Calculate (i) Lateral surface area and (ii) Total surface area.
Solution:
Radius of circular base (r) = 8 units
Height of cone (h) = 15 units
Let’s calculate the slant height (l).
l2 = h2 + r2
l2 = 82 + 152
l2 = 64 + 225
l2 = 289
∴ l $= \sqrt{289} = 17$ units
- Lateral surface area = πrl = 3.14 × 8 × 17
Lateral surface area = 427.04 units2
- Total surface area = πr(l + r)
Total surface area = 3.14 × 8 × (17 + 8)
Total surface area = 3.148 × 25
Total surface area = 628 units2
- Find the volume of a right circular cone with a radius of 21 in and a height of 5 in.
Solution:
Radius (r) = 21 in
Height (h) = 5 in
We know that volume of a right circular cone $= \frac{1}{3} \pi r^{2}h$
$V = \frac{1}{3} \times \frac{22}{7} \times 21^{2} \times 5$
$V = \frac{1}{3} \times \frac{22}{7} \times 21^{2} \times 5 = 6930$ in3
Hence, the volume of the given cone is 6930 in3.
Practice Problems on Right Circular Cone
Right Circular Cone – Definition, Properties, Formulas, Examples
Which of the following are parts of a right circular cone?
Radius, height, and slant height is the part of a right circular cone.
What is the total surface area of a right circular cone of radius r and slant height l?
The total surface area of a right circular cone of radius r and slant height l is given by πr(l + r).
If a right circular cone has a base radius of 4 inches and a height of 3 inches, then what is its slant height?
Slant height is given by: $l^{2} = h^{2} + r^{2}$
$l^{2} = 3^{2} + 4^{2} = 25$
Therefore, l = 5 inches
The volume of a right circular cone is equal to one-third of the product of the area of the _____ and its height.
The volume of a right circular cone is equal to one-third of the product of the area of the circular base and its height.
The frustum of a cone is formed when a right circular cone is cut by a plane that is parallel to the ______ of the cone.
The frustum of a cone is formed when a right circular cone is cut by a plane that is parallel to the “base” of the cone.
Frequently Asked Questions about Right Circular Cone
How many edges and vertices does a right circular cone have?
A right circular cone has one curved edge and one vertex. The pointed vertex at the top of the cone is also called “apex.”
Is the right circular cone a polyhedron?
No, the right circular cone is not a polyhedron. Polyhedrons are three-dimensional geometric shapes with flat, polygonal faces. A cone, including the right circular cone, has curved, non-polygonal surfaces and a single curved face, making it distinct from polyhedra.
What is the difference between a right circular cone and a cone?
The apex of a right circular cone is positioned directly above the center of its base. This alignment results in a line that runs from the apex to the base’s center, forming a right angle with the cone’s radius. In contrast, for a general cone, the apex can be located at any point.
How do you find the slant height of a right circular cone?
The slant height of a right circular cone can be determined using the formula $l^{2} = h^{2} + r^{2}$.Where, r = radius, h = height, and l= slant height.
What is the formula for finding the surface areas of a right circular cone?
(i) Curved surface area of right circular cone = π r l
(ii) Total surface area of a right circular cone = πr(r + l)
How do you find the volume of a cone if radius and slant height are given?
If the radius(r) and slant height(l) of a cone is given, then first find the height of the cone. Then apply the formula: Volume of a right circular cone $= \frac{1}{3}πr^{2} h$.






















