- What Is the Slope of Perpendicular Lines?
- Formula for Finding the Slope of Perpendicular Lines
- How to Find the Slope of a Line Perpendicular to the Given Line
- Solved Examples on Slope of Perpendicular Lines
- Practice Problems on Slope of Perpendicular Lines
- Frequently Asked Questions about Slope of Perpendicular Lines
What Is the Slope of Perpendicular Lines?
The slopes of two perpendicular lines are negative reciprocals of each other. In simple words, the product of the slopes of two perpendicular lines equals -1.
Two lines are said to be perpendicular if they intersect each other at a right angle (90).

Recommended Games
Formula for Finding the Slope of Perpendicular Lines
If the slopes of the two perpendicular lines are m1 and m2, then the relationship between the slopes is given by the formula
$m_{1} \times m_{2} = -1$
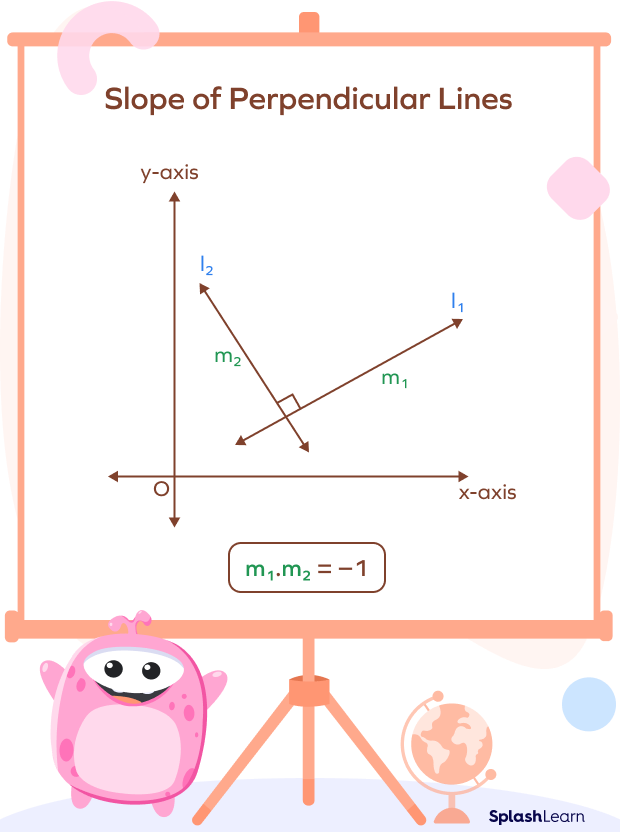
Slope of Perpendicular Lines: Negative Reciprocals
The slopes of perpendicular lines are negative reciprocals of each other. Thus, the slope of a line perpendicular to a given line is the negative reciprocal of the slope of the given line.
A reciprocal is defined as the multiplicative inverse of a given number. The multiplicative inverse (or reciprocal) of a non-zero number “a” is written as $\frac{1}{a}$.
To obtain the negative reciprocal of a particular value, just add a minus sign to its reciprocal. So, the negative reciprocal of “a” can be written as $\frac{-1}{a}$.
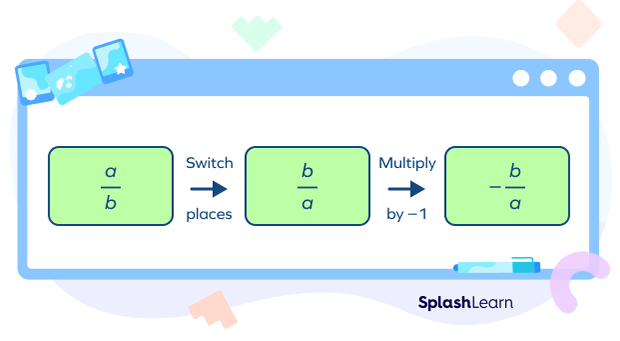
How to Find the Slope of a Line Perpendicular to the Given Line
If the slope of one line is known, the slope of the line perpendicular to it is calculated as the negative reciprocal of the first line.
The general form of the equation of a line is given as
$ax + by + c = 0$
Convert this equation into the slope-intercept form of the equation of a line.
$y = \frac{-ax}{b} \;-\; \frac{c}{b}$
So, we get the slope for the line would be
$m_{1} = -\;\frac{a}{b}$
The general formula for the slope of perpendicular lines is
$m_{1} . m_{2} = -1$
$\Rightarrow -\;\frac{a}{b} . m_{2} = -\;1$
$\Rightarrow m_{2} = \frac{b}{a}$
Therefore, the slope of the perpendicular line would be $\frac{b}{a}$.
Example: Find the slope of a line perpendicular to the line $y = -\;2x + 1$.
Given line: $y = -\;2x + 1$.
Slope of the given line $= m = -\;2$
Slopes of perpendicular lines are negative reciprocals of each other.
Thus, slope of the line perpendicular to the given line is $-\;\frac{1}{-\;2} = \frac{1}{2}$.
Derivation of the Formula for Finding the Slope of Perpendicular Lines
The angle between the two lines with slopes m1 and m2 is obtained using the formula
tan $\theta = \frac{m_{1}-m_{2}}{1 + m_{1} m_{2}}$
If two lines are perpendicular, then $\theta = 90^{\circ}$.
tan $90^{\circ} = \frac{m_{1}-m_{2}}{1 + m_{1}m_{2}}$
Note that tan $90^{\circ}$ is not defined.
$\infty = \frac{m_{1}-m_{2}}{1 + m_{1}m_{2}}$
Thus, $1 + m_{1} m_{2} = 0$
$m_{1} m_{2} = -1$
What Is the Slope of Parallel Lines and Perpendicular Lines?
- If two lines are parallel, they have the same slope. In other words, the slopes of two parallel lines are equal.
If lines l and m are parallel, such that the slope of line l is m1 and the slope of line m is m2, then
$m_{1} = m_{2}$.
- On the other hand, the slopes of two perpendicular lines are negative reciprocals of each other.
If lines l and m are perpendicular, such that the slope of line l is m1 and the slope of line m is m2, then
$m_{1} m_{2} = -\;1$
or
$m_{1} = \frac{-1}{m_{2}}$
Facts about Slope of Perpendicular Lines
- Perpendicular lines form right angles at the point they intersect.
- If two lines are parallel, their slopes are equal.
- If the slope of a line is m, the slope of the line perpendicular to it is -1m.
- A vertical line line is always perpendicular to a horizontal line.
Conclusion
In this article, we learned how to find the slope of perpendicular lines, the associated formula, and its derivation. Let’s solve a few examples and practice MCQs on these concepts for better comprehension.
Solved Examples on Slope of Perpendicular Lines
Example 1: What will be the slope of the line perpendicular to the line $6x – 2y = 4$?
Solution:
Given line: $6x – 2y – 4 = 0$
$6x – 2y = 4$
$\Rightarrow -\; 2y = 4\;-\;6x$
$\Rightarrow y = 3x\;-\;2$
Slope of the first line $= m_{1} = 3$
Slope of the perpendicular line $= \frac{-1}{m_{1}}$
$\Rightarrow m_{2} = -\;\frac{1}{3}$
Therefore, the slope of the perpendicular line would be $-\;\frac{1}{3}$.
Example 2: What will be the equation of a line passing through the point (5, 2) and with the slope of the perpendicular line equal to -3?
Solution:
The slope of the perpendicular line is $m_{1} = \;-\;3$.
From the formula of the slope of the perpendicular lines
$m_{1} .m_{2} = -1$
$\Rightarrow -\;3 \times m_{2} = -\;1$
$m_{2} = \frac{1}{3}$
The line passes through the point $(x_{1},\; y_{1}) = (5,\; 2)$ and has slope $m = \frac{1}{3}$.
To find the equation of the required line, we will use the slope-point form.
$(y\;-\;y_{1}) = m(x\;-\;x_{1})$
$\Rightarrow (y\;-\;2) = \frac{1}{3} (x \;-\;5)$
$\Rightarrow 3(y\;-\;2) = 1(x\;-\;5)$
$\Rightarrow 3y\;-\;6 = x\;-\;5$
$\Rightarrow x\;-\;3y + 6\;-\;5 = 0$
$\Rightarrow x\;-\;3y +1 = 0$
Therefore, the equation of the line is $x\;-\;3y + 1 = 0$.
Example 3: Find the slope of a line perpendicular to the line passing through points (1, 2) and (3, 4).
Solution:
Slope of a line passing through the points $(x_{1},\;y_{1})$ and $(x_{2},\;y_{2})$ is given by
Slope $= \frac{y_{2}-y_{1}}{x_{2}-x_{1}}$
Here, $(x_{1},\;y_{1}) = (1,\; 2)$ and $(x_{2},\;y_{2}) = (3,\; 4)$
Slope $= \frac{4 – 2}{3 – 1}$
$m = \frac{2}{2} = 1$
Slope of the required line $= \frac{-1}{m} = -\;1$
Practice Problems on Slope of Perpendicular Lines
Slope of Perpendicular Lines - Definition, Formula, Examples, FAQs
What is the slope of the line perpendicular to the line whose slope is $\frac{6}{7}$?
$m_{1}.m_{2} = -\;1$
$\Rightarrow \frac{6}{7} \times m_{2} = -\;1$
$\Rightarrow m_{2} = -\;\frac{7}{6}$
Find the slope of the line perpendicular to $3x \;-\;4y + 5 = 0$.
$3x \;-\;4y + 5 = 0 \;m_{1} = -\;\frac{a}{b} \Rightarrow m_{1} = -\;\frac{3}{-4} = \frac{3}{4}$.
$\Rightarrow m_{1} m_{2} = -\;1$
$\Rightarrow \frac{3}{4} \times m_{2} = -\;1$
$\Rightarrow m_{2} = -\;\frac{4}{3}$
Slopes of perpendicular lines are
Slopes of perpendicular lines are negative reciprocals of each other.
If the slopes of two perpendicular lines are m and n, then
If the slopes of two perpendicular lines are m and n, then $mn = -\;1$.
Frequently Asked Questions about Slope of Perpendicular Lines
Do perpendicular lines have the same slope?
Perpendicular lines do not have the same slope. The slopes of the perpendicular line are negative reciprocals of each other.
What is the slope of parallel lines?
The slope of parallel lines is equal to each other. Any lines that are parallel to each other have the same slope but different y-intercepts.
How do you identify perpendicular lines from slopes?
If the product of slopes is -1, the two lines are perpendicular.
How do you describe the slopes of perpendicular lines?
The slopes of two perpendicular lines are negative reciprocals of each other. If the slope of a line is m, the slope of the line perpendicular to it is the negative reciprocal of m, given by $\frac{-1}{m}$.


























