What Is Meant by Subtracting Integers in Math?
Subtracting integers is the method of finding the difference between two integers. These two integers may have the same sign or different signs. The set of integers is represented by
Z={…,-3,-2,-1,0,1,2,3,…}.
If we subtract the integer b from the integer a, we write it as a – b.
Example: Subtract 7 from 9.
9 – 7 = 2
We can also write every subtraction problem as an addition problem. Replace the – sign by + sign, and replace the second integer by its additive inverse. This can be written symbolically as
a – b = a + (-b)
Finally, you can find the answer using the rules for adding integers.
Additive inverse of an integer is written by simply removing its sign, keeping only the numerical value.
Examples:
Additive inverse of 7 is -7.
Additive inverse of -9 is 9.
Recommended Games
Subtracting Integers: Definition
Subtracting integers is the method of finding the difference between two integers having the same or different signs.
Subtraction of integers can be written as the addition of the first number and the additive inverse of the second number.
Recommended Worksheets
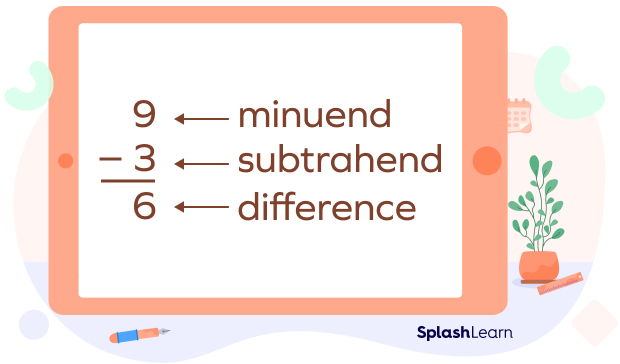
Subtrahend and Minuend
When we subtract one number from another, the number being subtracted is called subtrahend, the first number is called minuend.
Rules for Adding Integers
Any addition fact can be written as a subtraction fact. Also, any subtraction fact can be written as an addition fact. So, the rules for adding integers and the rules for subtracting integers correspond to each other.
| Rules for Adding Integers | |||
| Case | Addition Expression | Result | Example |
| Positive integer + Positive integer | (+a) + (+b) | +(a + b) | 5 + 7 = 12 |
| Negative integer + Negative integer | (-a) + (-b) | -(a + b) | (-7)+(-5)=-(7+5)=-12 |
| Negative integer + Positive integer | (-a) + (+b) | +(b – a) or -(a – b) | (-7)+5=-(7-5)=-2 |
| Positive integer + Negative integer | (+a) + (-b) | +(a – b) or -(b – a) | 7+(-5)=7-5=2 |
Rules for Subtracting Integers
| Description | Rule |
|---|---|
| Subtraction involving 0: | If we subtract 0 from any integer, the answer will be the integer itself.a – 0 = aIf we subtract any integer from 0, we will find the additive inverse or the opposite of the integer. 0 – a = -a |
| Subtracting a smaller integer from a larger integer: | If you subtract a smaller integer from a larger integer, the sign of the result will be positive. |
| Subtracting a larger integer from a smaller integer: | If you subtract a larger integer from a smaller integer, the sign of the answer will be negative. |
| Expressing subtraction using addition: | Subtraction of two integers can be written as sum of the first integer and the additive inverse of the second integer.a – b = a + (-b)Use the rules for adding integers to find the answer. |
| Subtraction of two positive integers: | When subtracting two positive integers, first subtract the smaller number from the larger number. The sign of the final answer will bei) positive when subtracting a smaller number from a larger number18-5 =13ii) negative when subtracting a larger number from a smaller number5-18=-13 |
| Subtraction of two negative integers: | When subtracting two negative integers, change the subtraction sign to addition and change the sign of the second number. Next, perform the addition using the rules for adding integers.Examples: (-9)-(-3)=(-9)+3=-(9-3)=-6(-1)-(-4)=(-1)+4=4-1=3 |
| Subtracting integers with different signs: | Change the middle – sign to + sign and replace the second number by its additive inverse. Next, perform the addition using the rules for adding integers. Here, we have two cases. i) Negative Integer – Positive Integer = The result is always negative.Here, the result will always have a negative sign since we are subtracting a larger number from a smaller number.Example: (-5) -( 2) = (-5) + (-2) = -7 ii) Positive Integer – Negative Integer = The result is always positive.Here, the result will always have a positive sign since we are subtracting a larger number from a smaller number.Example: 9-(-3)=9+3=12 |
Table of Rules for Subtracting Integers
| Signs of integers | What to do? | Sign of the answer | Examples |
|---|---|---|---|
| (+) – (+) | Subtract | Sign of the larger integer | 9-4=54-7=-3 |
(-) – (-) | Subtract | Sign of the larger integer | (-9)-(-5)=-9+5=-4 |
(+) – (-) | Add | + | (7) – (-2)=7+2=9 |
| (-) – (+) | Add | – | (-1) – (8)=(-1)+(-8)=-9 |
How to Subtract Integers
The most simple rule to remember when subtracting integers is to convert the problem as the addition problem and use the rules for adding integers.
- Subtracting Integers with the Same Sign: Let’s understand how to subtract integers with the same signs.
i) Positive integer – Positive integer
Here, the order of the numbers is important to decide the sign of the answer.
The answer of the result will be positive when subtracting a smaller number from a larger number.
8-1=7
30 – 13 = 17
The answer of the result will be negative when subtracting a larger number from a smaller number.
4 – 7 = -3
1-5=-4
ii) Negative integer – Negative integer
Change the problem to an addition problem and follow the rules for addition of integers.
(-5)-(-1) = (-5)+1 =-4
(-2) – (-5) = -2 + 5 = 3
- Subtracting Integers with Different Signs: Now, let’s understand how to subtract integers with different signs with examples.
i) Positive Integer – Negative integer
It is clear that we are subtracting a smaller value from a larger value. So, the answer will always be positive in this case.
5-(-1) = 5 + 1 = 6
2 – (-5) = 2 + 5 = 3
ii) Negative Integer – Positive Integer
It is clear that we are subtracting a larger value from a smaller value. So, the answer will always be negative in this case.
(-1)-5 = (-1) + (-5) = -6
(-2) – (5) = (-2) + (-5) = -7
Properties of Subtraction of Integers
There are some properties related to the subtraction of integers. They are as follows:
- Closure property: The subtraction of any two integers is an integer. For any two integers a and b, the difference a -b is also an integer.
- Commutative property: Subtraction of integers is not commutative. For any two integers a and b, we have a – b b – a.
2 – 4 4 – 2 and -6 – (-3 ) -3 – (- 6)
- Associative property: The subtraction of integers is not associative. That is, for any three integers a, b and c, we have, a -(b – c) (a – b) – c
For example, 2 – ( 5 – 3) = 2 – 2 = 0
(2 – 5) – 3 = – 3 – 3 = – 6 ,
Here, 0 6
- Identity property: We have a – 0 = a , for any integer a indicating that 0 is correct identity for subtraction.vIt’s important to note that 0 – a a is not the left identity
Subtracting Integers on a Number Line
- Every subtraction fact can be written as an addition fact.
- Adding a positive integer is done by moving towards the right side (or the positive side) of the number line.
- Adding a negative integer is done by moving towards the left side (or the negative side) of the number line.
- Any one of the given integers can be taken as the base point from where we start moving on the number line.

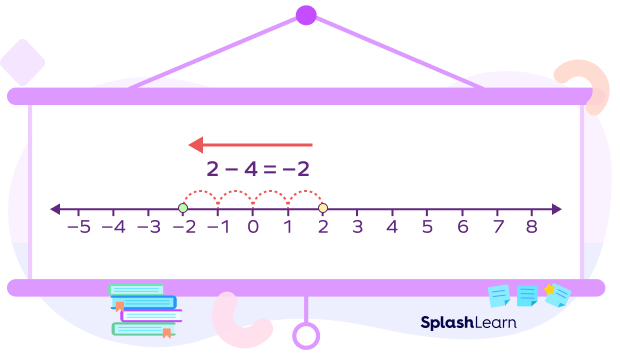
Example: Subtract 4 from 2.
We have to find 2 – 4.
Express 2 – 4 as the addition fact.
2 – 4 = 2 + (-4).
Locate integer with greater absolute value, 2.
Start from 2, take 4 jumps to the left side as we are subtracting 4 to 2.
Therefore, -2 is the required answer.
Facts about Subtracting Integers
- Integers are the negative numbers, zero, and positive numbers.
- Subtracting integers is the method of finding the difference between two integers with the same or different signs.
- To subtract two integers, add the opposite of the second integer to the first integer. This can be written symbolically as a
- – b = a + (- b)
- Adding a negative number is just like subtracting a positive number.
3 + (- 4) = 3 -(+4) - Subtracting a negative number is just like adding a positive number.
- 3 -(- 4) = 3 + 4
Conclusion
In this article, we learnt about subtraction of integers definition, rules, properties,steps and how to subtract integers on a number line. Let’s solve some examples and practice problems to understand the concept better.
Solved Examples on Subtracting Integers
Example 1: Subtract: –46 from –80.
Solution:
We have to subtract two negative integers.
Here, we have to find (-80) – (-46).
(-80) – (-46)
=-80 + 46
= -(80-46)
=-34
Example 2: Subtract: –8 from 7.
Solution:
Here, we have to subtract two integers with different signs.
Let’s write it in the form of an expression,
7 – (- 8 )
= 7 + 8
= 15
Thus, 7 – (- 8 ) = 15
Example 3: Find 1 – (– 5 ) using a number line.
Solution:
1 – (- 5 ) = 1 + 5
Start from 1 and take 5 jumps to the right.

Thus, 1 – (- 5 ) = 6
Practice Problems on Subtracting Integers
Subtracting Integers - Definition, Rules, Steps, Examples, Facts
Subtraction of integers can be written as the ________ of the opposite number.
Subtraction of integers can be written as the addition of the opposite number.
(-9)-(99)=
$(-9)-(99)=(-9)+(-99) = -108$
$1000 - (- 1)=$
$1000- (- 1) = 1000 + 1 = 1001$
When subtracting a positive integer from a negative integer, the answer will have
When subtracting a positive integer from a negative number, the answer will always have a negative sign since we subtract a larger number from a smaller number.
Which subtraction fact does the given number line represent?
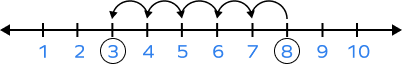
Starting from 8, we took 5 steps back and landed on 3. So, the image shows the equation
$8 \;-\; 5 = 3$
Frequently Asked Questions on Subtracting Integers
What are integers?
Integers include positive integers, negative integers, and zero. It is a number with no decimal or fraction part.
Set of integers = {…,−5,−4,−3,−2,−1, 0, 1, 2, 3, 4, 5,…}
What is a minuend and a subtrahend?
In a subtraction equation, minuend is the number from which another number would be subtracted. A subtrahend is the term that denotes the number being subtracted from another.
Does commutative property hold true for subtraction?
The commutative property does not hold for subtraction. It means for any two integers a and b, a – b ≠ b – a. For example, 2 – 4 ≠ 4 – 2
2 – 4 = – 2 and 4 – 2 = 2 and -2 ≠ 2
Thus, commutative property does not hold true for subtraction.
Does Associative property hold true for subtraction?
The associative property does not hold for subtraction. It means for any three integers a, b, and c, a -(b – c) ≠ (a – b) – c
For example, 2 – ( 5 – 3) = 2 – 2 = 0
(2 – 5) – 3 = – 3 – 3 = – 6 ,
Here, 0 6
Thus, associative property does not hold true for subtraction.




































