Supplementary Angles – Definition, Types, Facts, Examples, FAQs

What Are Supplementary Angles?

Two angles are said to be supplementary when the sum of angle measures is equal to 180. 

Note that the two angles need not be adjacent to be supplementary. So, what do supplementary angles look like? Take a look!

“Supplementary angles” that are “not adjacent”	“Supplementary angles” that are “adjacent”
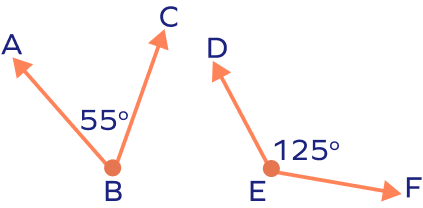They simply add up to 180 degrees. 55° + 125° = 180°	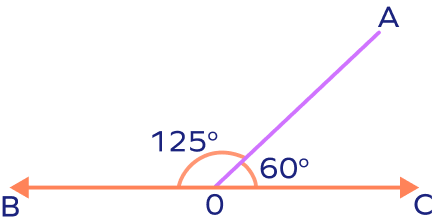Adjacent supplementary angles form a straight line and add up to 180 degrees.60° + 120° = 180°

Supplementary Angles: Definition

Supplementary angles can be defined as a pair of angles that add up to 180°.

Properties of Supplementary Angles

• Supplementary angles are a pair of angles that add up to 180°.
• One supplementary angle equals the difference between 180° and the other supplementary angle.
• The adjacent angles formed by two intersecting lines are always supplementary.
• Angles in a linear pair are always supplementary, but two supplementary angles need not form a linear pair.
• Adjacent supplementary angles form a straight line.

What Are Adjacent and Non-adjacent Supplementary Angles?

The supplementary angles can be both non-adjacent or adjacent. What does a supplementary angle look like? Let us move forward to learn about the two types of supplementary angles.

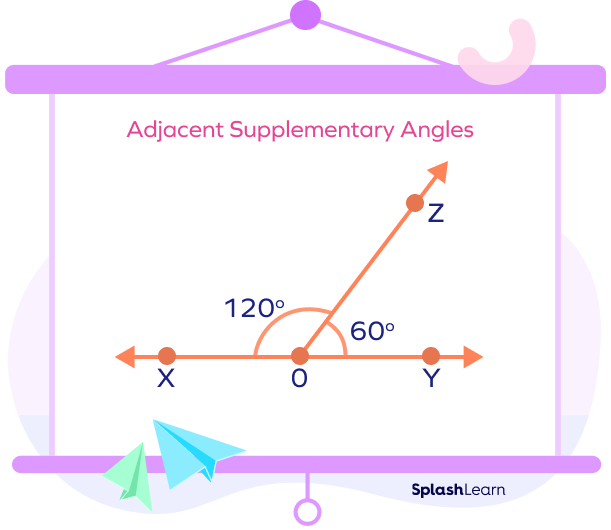
Adjacent Supplementary Angles:

The adjacent supplementary angles are the supplementary angles that share a common vertex and a common side. The angles together form a straight angle (and thus, a straight line). They are also called ‘angles in a linear pair’ or ‘linear pair of angles.’

Example: Consider the following diagram. The angles ∠XOZ and ∠YOZ are adjacent supplementary angles. They share a common vertex O and a common side OZ. 

Also, 60° + 120° = 180°

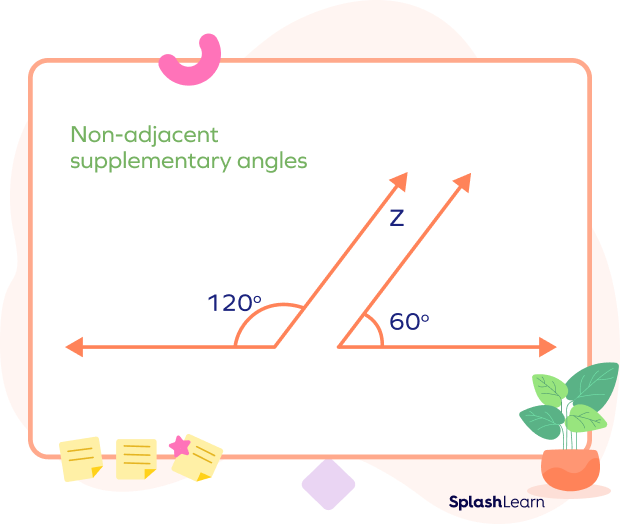
Non-Adjacent Supplementary Angles:

The non-adjacent supplementary angles are the angles which are not adjacent, but the sum of their measures equals 180 degrees. Any two angles whose sum is 180 degrees are supplementary!

How to Find Supplementary Angles

1. Measure the angles.
2. Add the measurements of the two angles and check if they add up to 180 degrees. 
3. The angles will be supplementary if the sum equals 180 degrees.

For two angles X and Y to be supplementary, we must have

m∠X + m∠Y = 180°

You can also find the other counterpart of a given angle to find two supplementary angles.

Example: What will be the supplementary angle of an angle of 70°?

We know that the sum of two supplementary angles should be 180°

Let us assume the missing angle to be x. 

70° + x = 180°

On solving for x, we get

x = 110°.

Supplementary Angles Theorem and Proof

Proof:

Suppose ∠x and ∠y are two different angles supplementary to a third angle ∠a.

∠x + ∠a = 180° …….(1)

∠y + ∠a = 180° …….(2)

From equations (1) and (2), we get

∠x + ∠a =  ∠y + ∠a

∠x = ∠y

Hence, proved.

Facts about Supplementary Angles

Conclusion

In this article, we learned about the supplementary angles, definition, properties, and also the theorem.We also discussed how to find supplementary angles. Let us move ahead to the numerical section to have a better comprehension of the concepts through solved examples and practice problems.

Solved Examples on Supplementary Angles

Example 1: Two angles are supplementary. Find the other angle if one angle is 80°.

Solution:

Let the missing angle be x.

x + 80° = 180° …Angles are supplementary.

Solving for x, we get

x = 100°

Therefore, the measure of the other supplementary angle is 100°.

Example 2: Two angles that are supplementary. One angle is 35° greater than the other. Find the missing angle.

Solution:

Let us assume that the measure of one angle is x°.

Then, other angle = x° + 35°

So, x° + (x° + 35°) = 180°

On simplifying:

2x° + 35° = 180°

2x°= 145°

x° = 72.5°

So, the other angle is:

x° + 35° = 72.5° + 35° = 107.5°

Therefore, 72.5° and 107.5° are the measures of the smaller and larger angles, respectively.

Example 3: What will be the measures of two supplementary angles if the first angle is three times the second angle?

Solution:

Let the smaller angle be x°.

Thus, the larger angle = 3x°.

x° + 3x° = 180° …Angles are supplementary.

On simplifying, we get

4x° = 180°

x° = 45°

So, the larger angle is:

3x° = 3(45°)

x° = 135°

Therefore, 45° and 135° are the values of the two supplementary angles.

Example 4: If two supplementary angles are in the ratio 3 : 2, find the measures of angles.

Solution: 

Let the measures of two angles be 3k° and 2k° respectively.

3k° + 2k° = 180°

5k° = 180°

k = 36

Now, we get the measures of the two angles.

3k° = (3 × 36)° = 108°

2k° = (2 × 36)° = 72°

Therefore, 108° and 72° are the measures of two supplementary angles.

Practice Problems on Supplementary Angles

Frequently Asked Questions about Supplementary Angles