Transitive Relations – Definition, Properties, Examples, FAQs

What Are Transitive Relations?

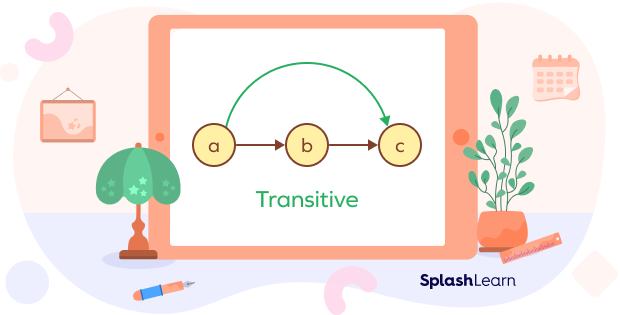
A relation is said to be a transitive relation, if “a is related to b” and “b is related to c” implies that “a is related to c.”

In other words, a relation is said to be a transitive relation, if the first element is related to the second element, and the second element is related to the third element in the set, then the first element must also be related to the third element.

Transitive Relation: Definition

A binary relation R defined on set A is considered a transitive relation, if for the elements a, b, and c in set A, (a, b) ∈ R, and (b, c) ∈ R implies that (a, c) ∈ R.

Examples of Transitive Relations

Let’s go through a few examples to understand the concept of transitive relations.

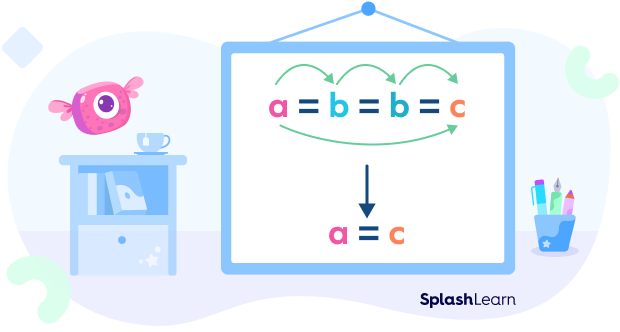
Example 1: The equality (=) relation defined on the set of real numbers is a transitive relation.

It is defined as 

aRb iff a = b.

or 

(a, b) ∈ R if and only if a = b.

We know that if a = b, and b = c, then a = c.

Thus, R is a transitive relation.

This is also known as the transitive property of equality. 

Example 2: “is subset of” is a transitive relation defined on the power set of a set.

We know that if A ⊆ B, B ⊆ C, then all the elements of A are also present in C.

Thus, A ⊆ C.

Thus, R is transitive.

Example 3: ‘Is less than‘ is a transitive relation defined on a set of real numbers. 

For any real numbers a, b, and c, we have 

If a < b and b < c, then a < c.

Similarly, the relations greater than (>), less than or equal to (), greater than or equal to () are also transitive. 

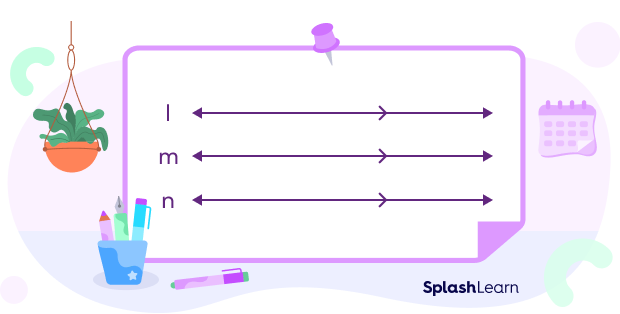
Example 4: “is parallel to” is a transitive relation defined on the set of straight lines.

If line l || line m, and line m || line n, then line l || line n.

Example 4: “Is divisible by: relation defined on the set of positive integers is a transitive relations.

If a is divisible by b, then a = bk for some positive integer k

If b is divisible by c, then b = ct for some positive integer t.

We get a = c(kt) for some positive integer kt

Thus, a is divisible by c.

Let R = {(g, h), (h, i), (g, i)} represent a transitive relation on the set A ={g, h, i}.

Here, (a, b) ∈ R, (b, c) ∈ R ⇒ (a, c) ∈ R    for all a, b ∈ A.

g is related to h, and h is related to i. 

For R to be transitive, g must be related to i.

The element (g, i) is also present in R.

Thus, R is transitive.

Anti-transitive Relation and Intransitive Relation

Anti-transitive Relation

• In anti- transitive relation, if (a, b) ∈ R and (b, c) ∈ R, then it implies that (a, c) ∉ R.
• An anti-transitive relation is a relation that violates the transitive property (a relation that does not satisfy transitive property).
• In an anti-transitive relation, if element a is related to element b, and element b is related to element c, then it implies that element a is not related to element c.
• Here, the absence of a relationship between a and c is guaranteed based on the relationship between a and b, and b and c.

Intransitive Relation

• In intransitive relation, for some a, b, c in R, (a, b) ∈ R and (b, c) ∈ R, but (a, c) ∉ R. Such a conclusion does not necessarily follow for each set of a, b, and c.
• These relations lack a consistent transitive pattern.

Properties of Transitive Relations

• The inverse of a transitive relation is a transitive relation.
• The union of two transitive relations need not be transitive. 
• The intersection of two transitive relations is a transitive relation. 
• A transitive relation is an asymmetric relation if and only if it is irreflexive.
• Transitive relations can be reflexive, meaning that every element is only related to itself. Note that it is not a requirement for transitivity.

Facts about Transitive Relations

Conclusion

In this article, we learned about transitive relations, definition, their examples, and properties. Let’s solve a few examples based on transitive relations.

Solved Examples on Transitive Relations

Example 1: If R is a relation on the set  A = {2, 3, 4} given by R  = {(2, 3), (3, 4), (2, 4)}. Verify if R is transitive. 

Solution:

Let a = 2, b = 3, c = 4.

We have 

(a, b)  =  (2, 3) ∈ R,  (b, c)  =  (3, 4) ∈ R

(a, c)  =  (2, 4) ∈ R

Hence, R is transitive.

Example 2: If A = {1, 2, 3} and R represents a relation on the set A as R = {(1, 1), (2, 2), (3, 3), (1, 2)}. Find whether R is a transitive relation or not. 

Solution:

Relation R defined on the set A is transitive if for the elements a, b, and c in set A, 

(a, b) ∈ R, and (b, c) ∈ R implies that (a, c) ∈ R.

Let us check the given condition for each ordered pair.

(a, b)	(b, c)	(a, c)
(1, 1)	(1, 2)	(1, 2)
(2, 2)	–	–
(3, 3)	–	–
(1, 2)	(2, 2)	(1, 2)

From the above table, we clearly understand that R follows the transitive rule. 

Example 3: Find x if x = y and y = 5.

Solution:

The “is equal to” relation defined on the set of real numbers is transitive.

By the transitive property of equality, if a = b and b = c, then a = c.

Thus, if x = y and y = 5, we have x = 5 by the transitive property.

Example 4: Is the relation “is perpendicular to” defined on the set of straight lines transitive?

Solution:

If line m ⟂ line p, and line p ⟂ line n, it does not follow that line m is perpendicular to line n. 

Thus, the relation is not transitive.

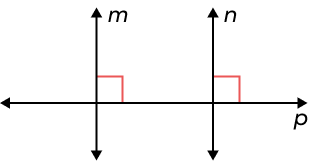
Practice Problems on Transitive Relations

Frequently Asked Questions about Transitive Relations