What Are the Types of Polynomials?
The types of polynomials can be categorized:
- On the basis of degree.
- On the basis of the number of terms.
A polynomial is an algebraic expression with a finite number of terms composed of constants, variables, coefficients, and exponents, which are connected by operations (addition, subtraction, multiplication, and division but no division by a variable), such that variables only have positive integral powers. Variables are also known as “indeterminates.”
| Examples of polynomials | Non-examples of polynomials |
|---|---|
| $g(x) = 2x^{2} + 9x \;-\;8$ | $x\;-\;5$ |
| $x^{3}y\;-\;xy \;-\;8$ | $\frac{1}{x \;-\; 1}$ |
| $z + 1$ | $5\sqrt{x}y\;-\;6$ |
Recommended Games
Degree of a Polynomial
The degree of a polynomial with a single variable can be defined as the highest exponent of the variable. A polynomial is said to be in the standard form when we write its terms from the highest to the lowest degree.
Example: The polynomial is $x^{3} + 4x^{2} + 3x\;-\;1$ has four terms, and the greatest exponent of x is 3. Thus, the degree of the polynomial is 3.
In case of a polynomial having more than one variable, the degree of the polynomial is the greatest number among the sums of the exponents of all variables in each term present in the polynomial.
Example: The polynomial $x^{3}y + 4x^{2} y \;-\; y^{2}$ has three terms. The degree of this polynomial is 4 because
Sum of exponents in the first term $= 3 + 1 = 4$
Sum of exponents in the second term $= 2 + 1 = 3$
Exponent in the third term $= 2$
Recommended Worksheets
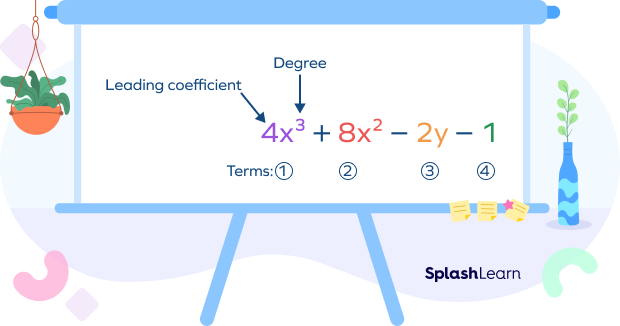
Parts of a Polynomial
The important parts of a polynomial are its degree, leading term, leading coefficient, and the constant term.
Example: Consider the polynomial, $x^{3} + 4x^{2} + 3x \;-\; 1$.
Degree: 3 (highest power in the polynomial)
Leading term: $x^{3}$ (the term containing highest power)
Leading coefficient: 1 (the coefficient of the leading term)
Constant term: -1 (the term/a number without a variable or $x^{0}$ term)
Types of Polynomials on the Basis of Degree
The degree of the polynomial is the highest power in the polynomial. Based on it, there are four major types of polynomials, zero or constant, linear, quadratic and cubic polynomial.
Zero Polynomial
It does not have a variable. It has no terms. The coefficient of all variables is zero. Its degree is not defined. Zero polynomial is of the form $P(x) = 0$.
Important Points to Remember:
- In general, $f(x) = c$ is known as a constant polynomial (degree of the polynomial is 0). A constant polynomial $f(x) = c$ with $c = 0$ is called a zero polynomial. The degree of zero polynomial is not defined.
- A zero polynomial and a zero-degree polynomial are different.
Zero-degree polynomial (constant polynomial) means the degree of all variables in the polynomial is 0. Zero polynomial is the polynomial in which the coefficients of all variables are 0.
Linear Polynomial
The degree of a linear polynomial is 1. It is of the form $f(x) = ax + b$.
Example: $x + y +3$
Quadratic Polynomial
Quadratic polynomials are the types of polynomials with degree 2. It is of the form $f(x) = ax^{2} + bx + c$.
Example: $4x^{2} + 3x \;-\; 1$
Cubic Polynomial
Cubic polynomial is the polynomial whose degree is 3. It is of the form $f(x) = ax^{3} + bx^{2} + cx + d$.
Example: $x3 + 4×2+ 3x \;-\; 1$
Types of Polynomials on the Basis of the Number of Terms
The terms of polynomials are the constituents in the polynomial equation separated by the mathematical operators. For instance, the polynomial $x^{3} + 4x^{2} + 3x \;-\; 1$ has four terms separated by three operators. Based on the number of terms, the main four types of polynomials are monomials, binomials, trinomials, and quadrinomials.
Monomials
Monomials are polynomials that contain only one non-zero term.
Examples: $3x ,\; x^{3},\;8$
Binomials
A binomial contains two terms.
Examples: $a^{2} + 1,\; x + y$
Trinomial
A trinomial contains three terms.
Examples: $4x^{2} + 3x \;-\; 1,\; x^{2} + 3y \;-\; 1$
Four-term Polynomial or Quadrinomial
It contains four terms.
Example: $x^{3} + 4x^{2} + 3x \;-\; 1$
The list continues based on the increase in the number of terms. The five-term polynomial has five different terms, and so on.
Special Types of Polynomials
Let’s discuss a few special types of polynomials.
Monic Polynomial
A polynomial in a single variable whose leading coefficient is 1 is called the monic polynomial.
Example: $x^{5} + 3x + 1$
Here, the leading term is $x^{5}$. The leading coefficient is 1.
Constant Polynomial
A constant polynomial is a polynomial whose degree is 0. Its graph is parallel to the x-axis. It is of the form $f(x) = k$, where k is a constant. When $k = 0$, it is called a zero polynomial.
Example: $f(x) = 6$
Irreducible Polynomial
A polynomial that cannot be factored into lower degree polynomials is called an irreducible polynomial.
Example: $x^{5}\;-\;3$ is irreducible over the set of real numbers.
However, $x^{2}\;-\;4$ is not an irreducible polynomial.
Homogeneous Polynomial
If each term in a polynomial has the same degree, then the polynomial is called a homogeneous polynomial.
Example: $x^{3} + 2x^{2} y + y^{3}$
Facts about Types of Polynomials
- Polynomials can not have an infinite number of terms.
- Polynomial equations are algebraic equations obtained by equating polynomials to 0.
Example: $x^{3} + 4x^{2} + 3x \;-\; 1 = 0$
Conclusion
In this article, we learned about different types of polynomials based on the degree and the number of terms. Let’s solve a few examples and practice problems to understand the concept better.
Solved Examples for Types of Polynomials
1. What is the degree and the leading coefficient of the polynomial $5x^{3} + 2x^{2} + 3c$? What type of polynomial is it?
Solution:
Given polynomial: $5x^{3} + 2x^{2} + 3c$
The degree of the polynomial $= 3$.
Leading term $= 5x^{3}$
Leading coefficient = The coefficient of the leading term $= 5$
Since the degree of the polynomial is 3, it is a cubic polynomial.
Since there are 3 terms in the polynomial, it is trinomial.
2. What is the degree and the type of the polynomial $f(x) = x$?
Solution:
The degree of the polynomial is defined as the highest power or exponent associated with the variable.
Thus, the degree of $f(x) = x$ is 1.
This is a linear polynomial.
Also, it is a monomial since there’s only a single term in the polynomial.
3. Categorize the given polynomials on the basis of degree and the number of terms.
- $x^{5}$
- $y^{2}\;-\;1$
- $x + y + z$
- $x^{2}y + x^{2} + y$
- 0
- 9
Solution:
| Polynomial | Category based on the degree | Category based on the number of terms |
|---|---|---|
| $x^{2}$ | Quadratic polynomial $(\text{degree} = 2)$ | Monomial (One term) |
| $y^{2}\;-\;1$ | Quadratic polynomial $(\text{degree} = 2)$ | Binomial (2 terms) |
| $x + y + z$ | Linear polynomial $(\text{degree} = 1)$ | Trinomial (3 terms) |
| $x^{2}y + x^{2} + y$ | Cubic polynomial$(\text{degree} = 3)$ | Trinomial (3 terms) |
| 0 | Zero polynomial $(\text{degree} = \text{not defined})$ | Monomial (One term) |
| 9 | Constant polynomial $(\text{degree} = 2)$ | Monomial (One term) |
Practice Problems on Types of Polynomials
Types of Polynomials: Monomial, Binomial, Trinomial, Examples, FAQs
The polynomial $x^{3} + 4x^{2} \;-\; 1$ is ___________.
Degree $= 3$ and Number of terms $= 3$
Thus, the polynomial is cubic and trinomial.
What is the type of $7x + 1$ on the basis of degree?
Degree $= 1$
Thus, the polynomial is linear.
Identify a monic polynomial.
A polynomial in a single variable whose leading coefficient is 1 is called the monic polynomial.
The number 2 can be written in a polynomial form as _____.
$2 = 2x^{0}$ since $x^{0} = 1$.
This is a constant polynomial.
Frequently Asked Questions on Types of Polynomials
Can we convert higher-order binomials to lower-order binomials?
Yes, we can convert higher-order binomials to lower-order binomials by factorization.
$x^{4}\;-\;16 = (x^{2}\;-\;4)(x^{2} + 4)=(x + 2)(x\;-\;2)(x^{2} + 4)$
How do we add polynomials?
To add two polynomials, we add like terms (terms having the same degree).
What are the polynomials with degree 4 called?
Polynomials with degree 4 are called bi-quadratic polynomials.
Can a monomial be a constant?
Yes, a monomial can be a constant.
Is zero polynomial a monomial?
Yes, 0 is a real number and a monomial can be a constant. Thus, zero polynomial is a monomial.


























