Universal Set in Math – Definition, Symbol, Examples, Facts, FAQs

What Is Universal Set in Math?

The universal set (symbol: U) is a set that contains all the elements of other related sets with respect to a given subject. It is a larger set that contains elements of all the related sets, without any repetition.

In mathematics, a set is defined as a collection of distinct, well-defined objects. 

Examples: the set of whole numbers, the set of months in a year, the set of positive even integers, etc. 

The universal set, as the term “universal” suggests, is the set containing all the relevant elements for the subject under discussion. It is the superset of all basic sets related to the given topic. 

Example: The set of real numbers is the universal set for the set of integers, the set of rational numbers, the set of natural numbers, and the set of whole numbers.

Consider an example in day-to-day life. If we are listing or studying animals, the universal set would be the set of all the animals in the world. The set of all animals in each country can be considered as a subset of this universal set.

Universal Set: Definition

The collection or set of all the elements in regard to a particular subject under discussion is known as a universal set.

Universal Set: Symbol

The capital letter “U” is usually used to denote a universal set. However, it is not a standard notation. The symbol “Ω” is also used to denote a Universal set. You can choose a symbol based on the topic at hand. 

Venn Diagram of Universal Set

A Venn diagram is an illustration or pictorial representation that uses circles to show the relationships among things. Circles that overlap or intersect show that there are common elements present while circles that do not overlap do not share any common traits.

Venn diagrams were created by mathematician John Venn and are widely used today in computer science, problem-solving, and set theory.

When drawing Venn diagrams, we use a rectangular box to represent the universal set. Circles are used to represent sets. All the subsets are drawn inside this box.

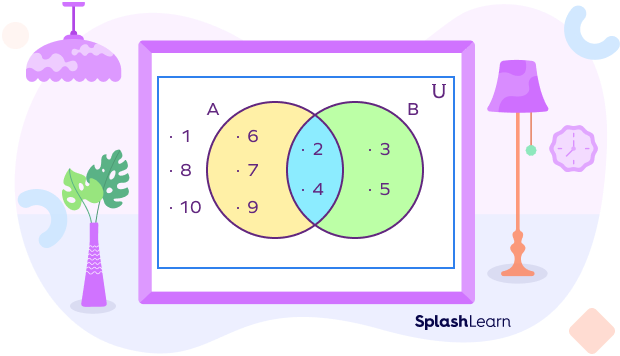
Consider the following example: 

Set $A = \left\{2, 4, 6, 7, 9\right\}$

Set $B = \left\{2, 3, 4, 5\right\}$

Universal Set $U = \left\{1, 2, 3, 4, 5, 6, 7, 8, 9, 10\right\}$

Difference Between Universal Set and Union of Sets

The universal set and the union of two or more sets can be confusing, but both these terms are different.

Universal Set

We know that a universal set is a set that contains all the elements of other sets and is represented by the symbol “U.”  

Union of Two Sets

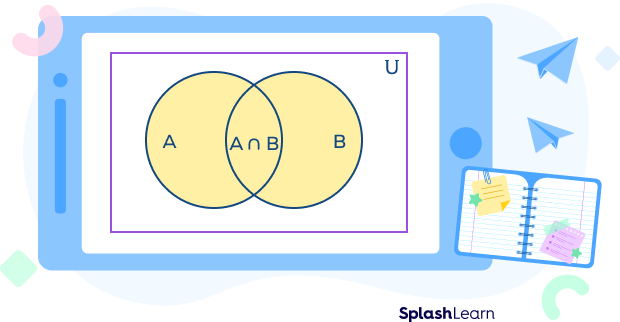
The union of two sets A and B is the set that contains elements that are either in A or in B or in both A and B. The union of two sets A and B is a new set represented by A ∪ B. 

In the Venn diagram shown below, the yellow shaded region represents the union of sets A and B. The entire rectangle with a purple border represents the universal set. It is represented by the letter “U” at the top right corner.

Example: Let’s consider three sets.

Set $A =$ Set of positive integers $= \left\{1, 2, 3, …\right\}$ 

Set $B =$ Set of negative integers $= \left\{\;-\;1, -2, \;-\;3, …\right\}$

Set $C = \left\{0\right\}$

The universal set for the sets A, B, and C is the set of integers given by

$U = \left\{…, \;-\;3, \;-\;2, \;-\;1, 0, 1, 2, 3, …\right\}$

The union of sets A and B is given by

$A \cup B = \left\{…, \;-\;3, \;-\;2, \;-\;1, 1, 2, 3, …\right\}$

Note that 0 is not present in the union of the sets A and B. However, it is present in the universal set.

Complement of Universal Set

Every set has a complement. The complement of a set contains all the elements from the universal set that are not present in the given set. Thus, if an element is present in a complement of a set, it is not present in the set.

The complement of the universal set is the empty set $\left(\text{symbol:}\; ∅\; \text{or} \left\{\right\}\right)$

Universal Set and Its Subsets

As the universal set contains all the elements of other sets, all related sets are subsets of the universal set. 

If every element in a set A is also an element in a set B, then A is a subset of B. The subset is represented by the symbol $\subseteq$. Note that the symbol $\subset$ is used to represent a proper subset.

$A \subseteq B$ is read as A is a subset of B.

Since every set is a subset of itself, the universal set is also a subset of itself.  

U $\subseteq$ U.

Example: Let the set of real numbers be the universal set. 

$U = \left\{ x | x\; \text{is a real number}\right\}$

We can list a few subsets as

U is a subset of itself.

Set of rational numbers is the subset of the set of real numbers.

Set of integers is the subset of the set of real numbers.

Set of natural numbers is the subset of the set of real numbers.

Set of whole numbers is the subset of the set of real numbers.

Facts about Universal Set

Conclusion

In this article, we have learned about the universal set, its complement and subsets. Let’s solve some universal set examples and practice problems for better understanding. 

Solved Examples on Universal Set

1. Assuming P is the set of positive odd integers and Q is the set of positive even integers, write the universal set of P and Q.

Solution: 

The sets P and Q can be written as:

$P = \left\{1, 3, 9…\right\}$ 

$Q = \left\{2, 4, 6…\right\}$

The universal set will be the set of positive integers (or natural numbers).

$U = \left\{1, 2, 3, 4, 5, 6, 7, 8, 9, 10…\right\}$

2. Draw a Venn diagram to represent the following sets:

$U = \left\{1, 2, 3, 4, 5, 6, 7, 8, 9\right\}, A = \left\{1, 2, 5, 6\right\}, B = \left\{3, 9\right\}$

Solution: 

Draw a rectangle and label it U to represent the universal set. Draw two circles within the rectangle to represent the sets A and B. Label the circles and write the given elements in each circle. Write the remaining elements of the universal set outside the circles but within the rectangle.

$A = \left\{1, 2, 5, 6\right\}$ 

$B = \left\{3, 9\right\}$

The elements 4, 7, and 8 are not in the sets A and B. We will show them in the universal set.

3. State whether the following statements are true or false.

1) Every set is a subset of itself.

2) An empty set is not a subset of the universal set.

3) The universal is the complement of an empty set.

Solution:

1) Every set is a subset of itself.

True 

2) An empty set is not a subset of the universal set.

False 

An empty set is a subset of every set.

3) The universal is the complement of an empty set.

True. 

The universal set and empty set are complements of each other.

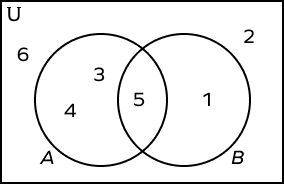
4. Observe the following Venn diagram and write down the universal set.

Solution:

Set $A = \left\{3, 4, 5\right\}$

Set $B = \left\{1, 5\right\}$

5 is common between both A and B.

The elements 2 and 6 are outside the sets A and B. 

Thus, the universal set $U = \left\{1, 2, 3, 4, 5, 6\right\}$

Practice Problems on Universal Set

Frequently Asked Questions on Universal Set