- What Is Addition and Subtraction of Fractions?
- Methods of Addition and Subtraction of Fractions
- Addition and Subtraction of Mixed Numbers
- Solved Examples on Addition and Subtraction of Fractions
- Practice Problems on Addition and Subtraction of Fractions
- Frequently Asked Questions on Addition and Subtraction of Fractions
What Is Addition and Subtraction of Fractions?
Addition and subtraction of fractions are the fundamental operations on fractions that can be studied easily using two cases:
- Addition and subtraction of like fractions (fractions with same denominators)
- Addition and subtraction of unlike fractions (fractions with different denominators)
A fraction represents parts of a whole. For example, the fraction 37 represents 3 parts out of 7 equal parts of a whole. Here, 3 is the numerator and it represents the number of parts taken. 7 is the denominator and it represents the total number of parts of the whole.
Adding and subtracting fractions is simple and straightforward when it comes to like fractions. In the case of unlike fractions, we first need to make the denominators the same. Let’s take a closer look at both these cases.
Recommended Games
Methods of Addition and Subtraction of Fractions
Before adding and subtracting fractions, we first need to make sure that the fractions have the same denominators.
When the denominators are the same, we simply add the numerators and keep the denominator as it is. To add or subtract unlike fractions, we first need to learn how to make the denominators alike. Let’s learn how to add fractions and how to subtract fractions in both cases.
Recommended Worksheets
Addition and Subtraction of Like Fractions
The rules for adding fractions with the same denominator are really simple and straightforward.
Let’s learn with the help of examples and visual bar models.
Addition of Like Fractions
Here are the steps to add fractions with the same denominator:
Step 1: Add the numerators of the given fractions.
Step 2: Keep the denominator the same.
Step 3: Simplify.
$\frac{a}{c} + \frac{b}{c} = \frac{a + b}{c}$ …$c \neq 0$
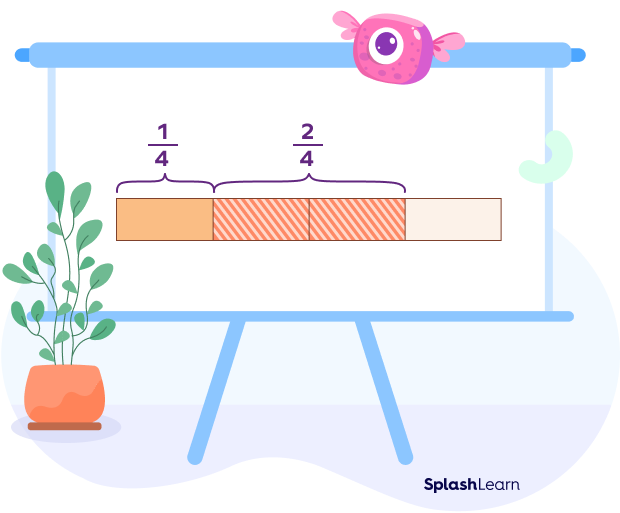
Example 1: Find $\frac{1}{4} + \frac{2}{4}$.
$\frac{1}{4} + \frac{2}{4} = \frac{1 + 2}{4} = \frac{3}{4}$
We can visualize this addition using a bar model:
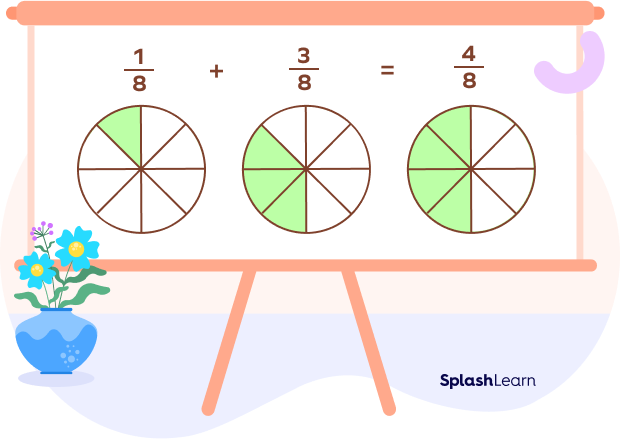
Example 2: $\frac{1}{8} + \frac{3}{8} = \frac{1 + 3}{8} = \frac{4}{8} = \frac{1}{2}$
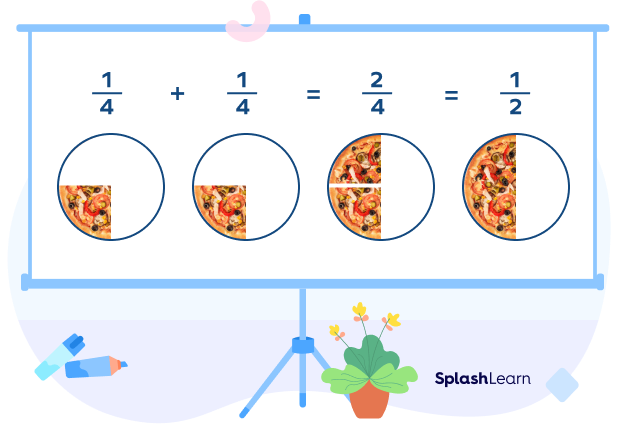
Example 3:
Subtraction of Like Fractions
Here are the steps to subtract fractions with the same denominator:
Step 1: Subtract the numerators of the given fractions.
Step 2: Keep the denominator the same.
Step 3: Simplify.
$\frac{a}{c}\;-\;\frac{b}{c} = \frac{a \;-\; b}{c}$ …$c \neq 0$
Example 1: Find $\frac{4}{6} \;-\; \frac{1}{6}$.
$\frac{4}{6}\;-\;\frac{1}{6} = \frac{4-1}{6} = \frac{3}{6} = \frac{1}{2}$
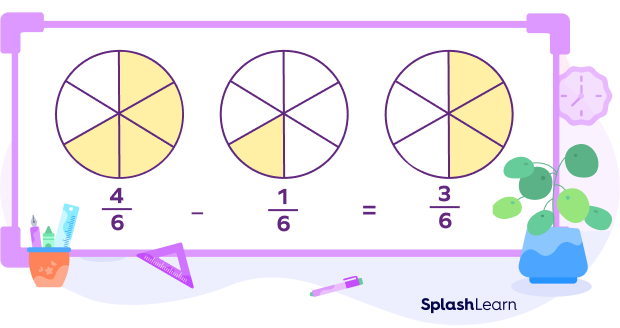
Example 2:
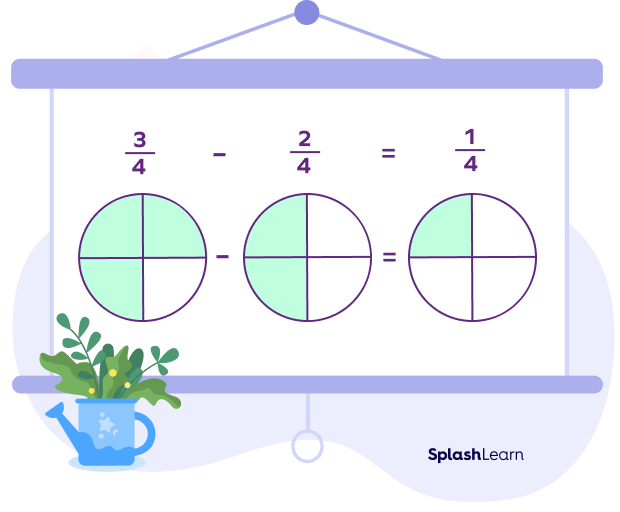
Addition and Subtraction of Unlike Fractions
Addition and subtraction of fractions with unlike denominators can be a little bit tricky since the denominators are not the same. So, we need to first convert the unlike fractions into like fractions. Let’s look at a few ways to do this!
Addition of Unlike Fractions
We can make the denominators the same by finding the LCM of the two denominators. Once we calculate the LCM, we multiply both the numerator and the denominator with an appropriate number so that we get the LCM value in the denominator.
Example: $\frac{3}{5} + \frac{3}{2}$
Step 1: Find the LCM (Least Common Multiple) of the two denominators.
The LCM of 5 and 2 is 10.
Step 2: Convert both the fractions into like fractions by making the denominators same.
$\frac{3 \times 2}{5 \times 2} = \frac{6}{10}$
$\frac{3 \times 5}{2 \times 5} = \frac{15}{10}$
Step 3: Add the numerators. The denominator stays the same.
$\frac{6}{10} + \frac{15}{10} = \frac{21}{10}$
Step 4: Convert the resultant fraction to its simplest form if the GCF of the numerator and denominator is not 1.
In this case, GCF (21,10) $= 1$
The fraction $\frac{21}{10}$ is already in its simplest form.
Thus, $\frac{3}{5} + \frac{3}{2} = \frac{21}{10}$
Subtraction of Unlike Fractions
Let’s learn how to subtract fractions when denominators are not the same. To subtract unlike fractions, we use the LCM method. The process is similar to what we discussed in the previous example.
Example: $\frac{5}{6} \;-\; \frac{2}{9}$
Step 1: Find the LCM of the two denominators.
LCM of 6 and $9 = 18$
Step 2: Convert both the fractions into like fractions by making the denominators same.
$\frac{5 \times 3}{6 \times 3} = \frac{15}{18}$
$\frac{2 \times 2}{9 \times 2} = \frac{4}{18}$
Step 3: Subtract the numerators. The denominator stays the same.
$\frac{15}{18} \;-\; \frac{4}{18} = \frac{11}{18}$
Step 4: Convert the resultant fraction to its simplest form if the GCF of the numerator and denominator is not 1.
In this case, the GCF (11,18) $= 1$
So, it is already in its simplest form.
Thus, $\frac{5}{6}\;-\; 29 = \frac{11}{18}$
Addition and Subtraction of Mixed Numbers
A mixed number is a type of fraction that has two parts: a whole number and a proper fraction. It is also known as a mixed fraction. Any mixed number can be written in the form of an improper fraction and vice-versa.
Adding and subtracting mixed fractions is done by converting mixed numbers into improper fractions.
Addition and Subtraction of Mixed Fractions with Same Denominators
The steps of adding and subtracting mixed numbers with the same denominators are the same. The only difference is the operation.
Step 1: Convert the given mixed fractions to improper fractions.
Step 2: Add/Subtract the like fractions obtained in step 1.
Step 3: Reduce the fraction to its simplest form.
Step 4: Convert the resulting fraction into a mixed number.
Example 1: $2\frac{1}{5} + 1\frac{3}{5}$
$2\frac{1}{5} = \frac{(5 \times 2) + 1}{5} = \frac{11}{5}$
$1\frac{3}{5} = \frac{(5 \times 1) + 3}{5} = \frac{8}{5}$
Thus, $2\frac{1}{5} + 1\frac{3}{5} = \frac{11}{5} + \frac{8}{5} = \frac{19}{5}$
Converting $\frac{19}{5}$ into a mixed number, we get
$\frac{19}{5} = 3\frac{4}{5}$
Example 2: $2\frac{1}{5} + 1\frac{3}{5} = \frac{11}{5} \;-\; \frac{8}{5} = \frac{3}{5}$
Addition and Subtraction of Mixed Fractions with Unlike Denominators
Step 1: Convert the given mixed fractions to improper fractions.
Step 2: Convert both the fractions into like fractions by finding the least common denominator.
Step 3: Add the fractions. (or subtract the fractions.)
Step 4: Reduce the fraction if possible or convert back to a mixed number
Let us understand the addition of mixed numbers with unlike denominators with the help of an example.
Example 1: Find the value of $1\frac{3}{5} + 2\frac{1}{2}$.
Convert the given mixed fractions to improper fractions.
$1\frac{3}{5} = \frac{8}{5}$ and $2\frac{1}{2} = \frac{5}{2}$
Step 2: Convert both the fractions into like fractions by making the denominators the same.
Here, LCM of 5 and 2 is 10.
Thus, $\frac{8 \times 2}{5 \times 2} = \frac{16}{10}$ and $\frac{5\times 5}{2 \times 5} = \frac{25}{10}$
Step 3: Add the fractions by adding the numerators.
$\frac{16}{10} + \frac{25}{10} = \frac{41}{10}$
Step 4: Convert back into a mixed number.
Thus, $\frac{41}{10}$ will become $4\frac{1}{10}$
Therefore, $1\frac{3}{5} + 2\frac{1}{2} = 4\frac{1}{10}$
Here’s an example for subtraction. It follows the same steps.
Example 2: $6\frac{1}{2} \;-\; 1\frac{3}{4}$
Step 1: Convert the mixed numbers into improper fractions.
$6\frac{1}{2} \;-\; 1\frac{3}{4} = \frac{13}{2} \;-\; \frac{7}{4}$
Step 2: Make the denominators equal.
LCM of 2 and 4 is 4.
$\frac{13 \times 2}{2 \times 2} = \frac{26}{4}$
Step 3: Subtract the fractions.
$\frac{26}{4} \;-\; \frac{7}{4} = \frac{19}{4}$
Step 4: Convert the fraction as a mixed number.
$\frac{19}{4} = 4\frac{3}{4}$
Thus, $6\frac{1}{2} \;-\; 1\frac{3}{4} = 4\frac{3}{4}$
Facts about Addition and Subtraction of Fractions
- We cannot add or subtract fractions without converting them into like fractions.
- Like fractions are fractions that have the same denominator, and unlike fractions are fractions that have different denominators.
- Equivalent fractions are two different fractions that represent the same value.
- The LCD (least common denominator) of two fractions is the LCM of the denominators.
Conclusion
In this article, we have learned about addition and subtraction of fractions (like fractions, unlike fractions, mixed fractions), methods of addition and subtraction of these fractions along with the steps. Let’s solve some examples on adding and subtracting fractions to understand the concept better.
Solved Examples on Addition and Subtraction of Fractions
- Solve: $\frac{2}{4} + \frac{1}{4}$.
Solution:
Here, the denominators are the same.
Thus, we add the numerators by keeping the denominators as it is.
$\frac{2}{4} + \frac{1}{4} = \frac{2 + 1}{4}$
$\frac{2}{4} + \frac{1}{4} = \frac{3}{4}$
2. Find the sum of the fractions $\frac{3}{5}$ and $\frac{5}{2}$ by using the LCM method.
Solution:
$\frac{3}{5}$ and $\frac{5}{2}$ are unlike fractions.
The LCM of 2 and 5 is 10.
Thus, we can write
$\frac{3}{5} + \frac{5}{2} = \frac{3 \times 2}{5 \times 2} + \frac{5 \times 5}{2 \times 5}$
$= \frac{6}{10} + \frac{25}{10}$
$= \frac{6}{10} + \frac{25}{10}$
$= \frac{31}{10}$
Thus, $\frac{3}{5} + \frac{5}{2} = \frac{31}{10}$
3. Find $\frac{4}{16} + \frac{5}{8}$.
Solution:
To add two fractions with different denominators, we first need to find the LCM of the denominators.
The LCM of 16 and 8 is 16.
Thus,
$\frac{4}{16} + \frac{5}{8} = \frac{4 \times 1}{16\times 1} + \frac{5 \times 2}{8 \times 2}$
$= \frac{10}{16} + \frac{4}{16}$
$= \frac{14}{16}$
$= \frac{7}{8}$
4. From a rope $12\frac{1}{2}$ ft. long, a $7 \frac{6}{8}\;-$ft-long piece is cut off. Find the length of the remaining rope.
Solution:
Total length of the rope $= 12\frac{1}{2}$ ft.
Length of the rope that was cut off $= 7 \frac{6}{8}$ ft.
The length of the remaining rope $= 12\frac{1}{2} \;-\; 7 \frac{6}{8}$
$12\frac{1}{2} \;-\; 7 \frac{6}{8} = \frac{25}{2} \;-\; \frac{62}{8}$
$= \frac{25 \times 4}{2 \times 4} \;-\; \frac{62 \times 1}{8\times 1}$
$= \frac{100}{8} \;-\; \frac{62}{8}$
$= \frac{38}{8}$
$= \frac{19}{4}$
Converting it into a mixed fraction, $\frac{19}{4}$ becomes $4 \frac{3}{4}$.
Thus, the length of the remaining rope is $4\frac{3}{4}$ ft.
Practice Problems on Addition and Subtraction of Fractions
Addition and Subtraction of Fraction: Methods, Examples, Facts, FAQs
Find $\frac{2}{4} + \frac{2}{4}$.
$\frac{2}{4} + \frac{2}{4} = \frac{4}{4} = \frac{1}{1} = 1$
$\frac{7}{24} + \frac{5}{16} =$
As the denominators are not the same, we first make denominators the same using the LCM method.
$\frac{7 \times 2}{24 \times 2} + \frac{5 \times 3}{16 \times 3} = \frac{14}{48} + \frac{15}{48}$
What is the least common denominator of $\frac{1}{2}$ and $\frac{1}{3}$?
$\frac{1}{2}$ and $\frac{1}{3}$ have different denominators. Thus, to make it the same, we find LCM of 2 and 3.
The LCM of 2 and 3 is 6.
Thus, the least common denominator is 6.
$\frac{3}{6} \;-\; \frac{1}{6} =$
As the denominators are the same, we only subtract numerators.
Thus, $\frac{3}{6} \;-\; \frac{1}{6} = \frac{2}{6} = \frac{1}{3}$
What equation does the following figure represent?
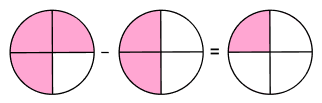
In the first circle, 3 out of 4 parts are shaded. So, the fraction is $\frac{3}{4}$.
In the second circle, 2 out of 4 parts are shaded. So, the fraction is $\frac{2}{4}$.
In the last circle, 1 out of 4 parts is shaded. So, the fraction is $\frac{1}{4}$.
Frequently Asked Questions on Addition and Subtraction of Fractions
How do we add and subtract negative fractions?
Negative fractions are simply fractions with a negative sign. The steps to add and subtract the negative fractions remain the same. We need to follow the rules for addition/subtraction with negative signs.
How can we convert an improper fraction into a mixed number?
To convert an improper fraction into a mixed number, we divide the numerator by the denominator. The denominator stays the same. The quotient represents the whole number part. The remainder represents the numerator of the mixed number.
Example: $\frac{14}{3} = 4\; \text{R}\; 2$
Quotient $= 4$
Remainder $= 2$
$\frac{14}{3} = 4\frac{2}{3}$
How do we divide two fractions?
To divide one fraction by another, we multiply the first fraction by the reciprocal of the second fraction.
$\frac{A}{B} \div \frac{C}{D} = \frac{A}{B} \times \frac{D}{C}$
For example, $\frac{1}{2} \div \frac{3}{5} = \frac{1}{2} \times \frac{5}{3} = \frac{5}{6}$
What are the rules of adding and subtracting fractions?
- Before adding or subtracting, we check if the fractions have the same denominator.
- If the denominators are equal, then we add/subtract the numerators keeping the common denominator.
- If the denominators are different, then we make the denominators equal by using the LCM method. Once the fractions have the same denominator, we can add/subtract the numerators keeping the common denominator as it is.
How do we add and subtract fractions with whole numbers?
- Convert the whole number to a fraction. To do this, give the whole number a denominator of 1.
- Convert to fractions of like denominators.
- Add/subtract the numerators. Now that the fractions have the same denominators, you can treat the numerators as a normal addition/subtraction problem.




































