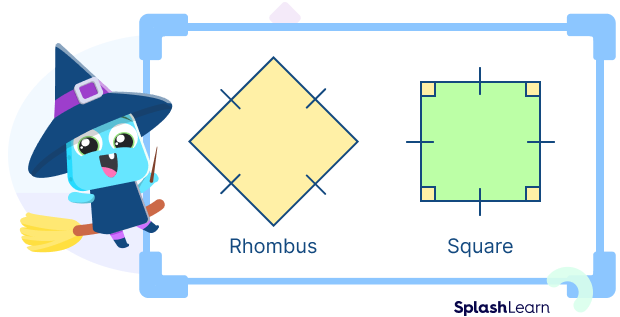
- What Is the Difference between a Rhombus and Square?
- Properties of a Rhombus and a Square
- What Is the Difference between a Rhombus and a Square?
- Solved Examples on the Difference between Rhombus and Square
- Practice Problems on the Difference between Rhombus and Square
- Frequently Asked Questions about the Difference between Rhombus and Square
What Is the Difference between a Rhombus and Square?
Rhombus and square are both quadrilaterals. To be more specific, rhombus and square are special types of parallelograms. Due to its specific angle characteristics, a square is a special type of rhombus where all sides are congruent. However, every rhombus is not a square.
Let’s take an overview of distinct characteristics of a rhombus and a square that set them apart:
| Aspect | Rhombus | Square |
|---|---|---|
| Side Lengths and Angles: | A rhombus has all sides of equal length, but its angles are not necessarily right angles (90 degrees). | A square has all sides of equal length and all angles of 90 degrees. |
| Symmetry: | A rhombus possesses 2 lines of symmetry. It also has rotational symmetry of 180 degrees (order 2). | A square has 4 lines of symmetry. It also has rotational symmetry of 90 degrees (order 4). |
| Diagonals: | The diagonals of a rhombus bisect each other at right angles. | The diagonals of a square are equal and bisect each other at right angles. |
| Interior Angles: | The interior angles of a rhombus can vary in size. | The interior angles of a square are all right angles (90 degrees). |
Recommended Games
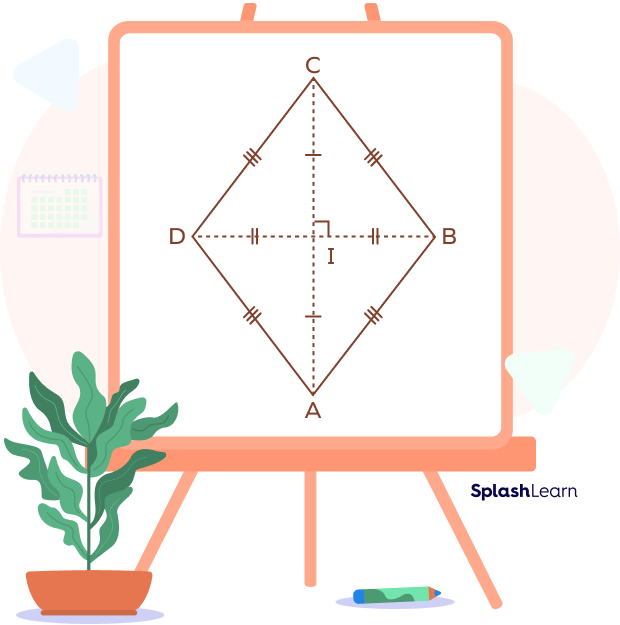
Rhombus: Definition
A rhombus is defined as a quadrilateral in which all sides are equal and opposite sides are parallel to each other.
Diagonals of a rhombus bisect each other at right angles. A rhombus is a special type of a parallelogram which has all sides equal.
In the rhombus ABCD, we have
AB = BC = AD = CD
Recommended Worksheets
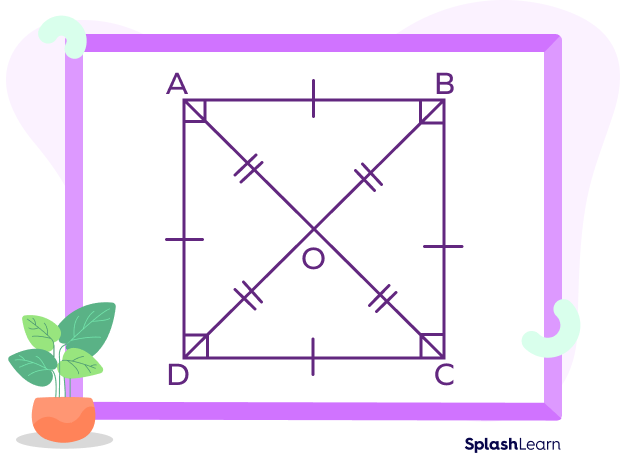
Square: Definition
A square is defined as a quadrilateral in which all sides are equal, opposite sides are parallel, and all angles are right angles.
Opposite sides of a parallelogram are equal and parallel whereas in a square opposite sides are parallel and all 4 sides are of the same length. Thus, a square is a special type of parallelogram with four right angles and with four equal sides.
We can also think of a square as a rectangle with equal length and breadth. It is a regular polygon with four equal sides and equal angles that measure 90° each. The diagonals of a square are equal and bisect each other at right angles.
In the square ABCD, AB = BC = AD = CD
Also, AC = BD
Properties of a Rhombus and a Square
Let’s discuss the properties of a rhombus and a square.
Properties of a Rhombus
- All sides of a rhombus are equal.
- Diagonals bisect each other at 90o.
- Opposite sides of a rhombus are parallel.
- Opposite angles are of a rhombus equal.
- All the interior angles of a rhombus add up to 360o.
- Adjacent angles of a rhombus add up to 180o.
Properties of a Square
- It has 4 sides and 4 vertices.
- Its sides are equal in length.
- All interior angles are equal and right angles, which means that each angle measures 90o.
- The sum of all the interior angles is 360o.
- Its two diagonals bisect each other at right angles.
- The diagonals of a square are of equal length.
What Is the Difference between a Rhombus and a Square?
The difference between a square and a rhombus is that all angles of a square are right angles, but the angles of a rhombus need not be right angles. So, a rhombus with right angles becomes a square. Every square is a rhombus, but each rhombus is not a square.
Difference between a Rhombus and a Square: Chart
| Rhombus vs. Square | |
|---|---|
| Rhombus | Square |
| The sides of a rhombus are not perpendicular to each other. | The sides of a square are perpendicular to each other. |
| A rhombus cannot be inscribed in a circle. | A square can be inscribed in a circle. |
| A rhombus has two lines of symmetry. | A square has four lines of symmetry. |
| Only the opposite angles of a rhombus are equal to each other. | All the angles of a square are equal and measure 90° each. |
| The diagonals of a rhombus are not equal. | The diagonals of a square are of equal length. |
Similarities between a Rhombus and a Square
- Both are quadrilaterals (special parallelograms).
- All sides are of equal length.
- Opposite sides are parallel.
- Diagonals are perpendicular to each other.
- The sum of all interior angles is 360 degrees.
- If the side equals “x” unit, the perimeter is given by “4a” units.
Rhombus and Square Formulas
Once we know the lengths and sides of the diagonals of rhombus and square, we can use them to find the area and perimeter of them. The formulas for area and perimeter of square and rhombus are as follows:
- Area of Rhombus and Square
i) For a square of side length “s”, the area is given by the formula:
Area of a square = side $\times$ side = s2
Where “s” = side of the square
ii) The formula for the area of a rhombus is:
Area of rhombus $= b \times h$ square units
where ‘b’ is the length of the base of the rhombus and “h” is the height of the rhombus.
iii) When length of the diagonals of a rhombus are known, then its area is given by half of their product.
Area of rhombus $= \frac{d_{1} \times d_{2}}{2}$ square units
where “d1” and “d2” are the diagonals of a rhombus.
- Perimeter of Rhombus and Square
i) The formula for the perimeter of a square is:
Perimeter of a square = side + side + side + side = 4s
where “s” is the side of the square.
ii) The formula for the perimeter of a rhombus is:
Perimeter of a rhombus $= 4 \times a$ units
where “a” is the length of the side of the rhombus.
Facts about Difference between Rhombus and Square
- Equal diagonals of a square make two similar isosceles triangles.
- A square has a larger area than all other quadrilaterals with the same perimeter.
- A rhombus has rotational symmetry of 180 degrees (order 2). That is, a rhombus retains its original orientation when rotated by an angle 180 degrees.
- The diagonals of a rhombus are the only 2 lines of symmetry that a rhombus has. These divide the rhombus into 2 identical halves.
- No inscribing and circumscribing circles can be made around the rhombus.
Conclusion
In this article, we have learned about properties of rhombus and square, and differences between them. It will help in understanding all the geometrical shapes related to a rhombus and square and how to calculate the area and perimeter of both. Let us apply the knowledge to solve some examples.
Solved Examples on the Difference between Rhombus and Square
1. What are some similarities between a square and a rhombus?
Solution:
| Square | Rhombus |
|---|---|
| A square is a quadrilateral. | A rhombus is a quadrilateral. |
| The diagonals of a square bisect each other at right angles. | The diagonals of a rhombus bisect each other at right angles. |
| The sum of the four interior angles of a square is 360o. | The sum of the four interior angles of a rhombus is 360o. |
| All the sides of a square are of equal length. | All the sides of a rhombus are also of equal length. |
| The opposite sides of a square are parallel. | The opposite sides of a rhombus are also parallel. |
2. The diagonals of a rhombus are 6 inches and 8 inches respectively. Find the area of rhombus.
Solution:
Length of one diagonal $d_{1} = 6$ in.
Length of the other diagonal $d_{2} = 8$ in.
We know that when two diagonals are known,
Area of rhombus $= \frac{d_{1} \times d_{2}}{2}$ square units
$A = \frac{6 \times 8}{2}$
$A = \frac{48}{2}$
$A = 24\; in^{2}$
Thus, area of rhombus $= 24\; in^{2}$
3. Find the height of the rhombus with an area of $315\; in^{2}$ and a perimeter of 180 in.
Solution:
The perimeter of rhombus $= 180$ in.
Therefore, side of rhombus $= \frac{Perimeter}{4} = \frac{180}{4} = 45$ in.
Now, Area of rhombus $= b \times h$
$315 = 45 \times h$
$h = \frac{315}{45}$
h = 7 in.
Therefore, the height of the rhombus is 7 in.
4. In rhombus ABCD, if ∠A = 70o, find the measure of all other angles.
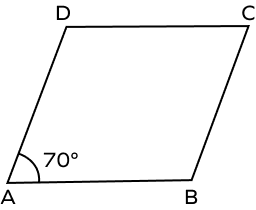
Solution:
∠A + ∠B = 180o (Adjacent angles of a rhombus add up to 180o.)
70o + ∠B = 180o (Given: ∠A = 70o)
∠B = 180o – 70o
∠B = 110o
∠C = ∠A = 70o (Opposite angles of a rhombus are equal.)
∠D = ∠B = 110o (Opposite angles are equal in a rhombus.)
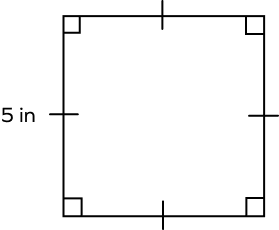
5. Find the area and perimeter of the following square.
Solution:
Perimeter of a square = side + side + side + side = 4s
Side of the given square = 5 in
Therefore, Perimeter $= 4 \times 5$ in
= 20 in
Area of a square = side $\times$ side = s2
$= 5 \times 5$
$= 25\; in^{2}$.
Practice Problems on the Difference between Rhombus and Square
Difference between Rhombus and Square - Example, Facts, FAQs
Which of the following statements is TRUE about the rhombus?
Opposite sides are parallel and opposite angles are equal in a rhombus.
Which of the following statements is NOT TRUE about the square?
The sum of all the interior angles is $360^{\circ}$.
In a square ABCD, the length of one diagonal is 4 in. The length of the other diagonal is ________.
The diagonals of the square are equal in length. Thus, if the length of one diagonal is 4 in, the length of the other diagonal is also 4 in.
The perimeter of the rhombus is 60 in. The side of the rhombus is ________.
Perimeter of a rhombus $= 4 \times a$ units
where “a” is the length of the side of the rhombus.
Thus, length of the side $= \frac{Perimeter}{4} = \frac{60}{4} = 15$ in.
In the square given below, if AE = 7 in, what is the measure of BE?
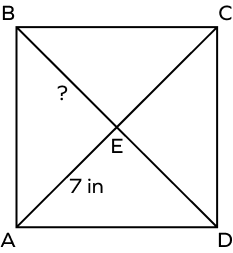
The diagonals of a square are equal in length and are perpendicular bisectors.
Thus, AC = BD and also, AE = CE = BE = DE.
As AE = 7 in, BE = 7 in
Frequently Asked Questions about the Difference between Rhombus and Square
Is a square a rhombus?
Yes, a square is a rhombus because a square has all the properties of a rhombus. Every square is a rhombus, but all rhombus are not squares.
Can a rhombus be a square?
Every rhombus is not a square. A rhombus becomes a square if it has four right angles or if its diagonals are equal.
If two squares have the same perimeter, will they have the same area?
Yes, if two squares have the same perimeter, it means that they also have the equal sides. This, in turn, implies that they also have the same area.
Is the side of a square and its diagonal the same length?
No, the side of a square and its diagonal aren’t of the same length. The diagonal of a square is greater in length than its side.
Does a rhombus have 4 right angles? Which rhombus has right angles?
A rhombus that has four right angles is a square. Otherwise, all angles of a rhombus are either acute or obtuse, but not right.
Why is every rhombus not a square?
A square has all of its angles equal to 90 degrees, but a rhombus does not.




































