Area of Irregular Shapes
Irregular shapes are polygons with five or more sides of varying lengths. These shapes or figures can be decomposed further into triangles, squares, and quadrilaterals to evaluate the area.
Some examples of irregular shapes are as follows:

Calculating the area of irregular shapes:
The approaches to estimating the area of irregular shape are:
Evaluating area using unit squares
Apply this technique for the shapes with curves apart from perfect circle or semicircles and irregular quadrilaterals. In this method, divide the shape into unit squares. The total number of unit squares falling within the shape determines the total area.

Count the square as “1” if the shaded region covers more than half while calculating the area for a more accurate estimate.

In the following figure, calculate the area by counting the unit squares, which is 6. If we denote each unit square in centimeter, the area will be 6 cm2.

- Dividing the irregular shape in two or more regular shapes
Use this method for irregular shapes, which are a combination of triangles and polygons. Use predefined formulas to calculate the area of such shapes and add them together to obtain the total area.
For example, an irregular shape we divide multiple edges into a triangle and three polygons.

The total area of the figure is given as:
⇒ Area = Area (ABIM) + Area (BCGH) + Area (CDEF) + Area (JKL)
⇒ Area = (AB × BI) + (BC × CG) + (CD × DE) + (1⁄2× LJ × KO)
⇒ Area = ( 10 × 5) + (3 × 3) + (2 × 2) + (1⁄2× 4 × 4)
⇒ Area = 50 + 9 + 4 + 8
⇒ Area = 71 cm2
- Dividing the irregular shape with curves in two or more regular shapes
In this method, decompose an irregular shape into multiple squares, triangles, or other quadrilaterals. Depending on the shape and curves, a part of the figure can be a circle, semicircle or quadrant as well.
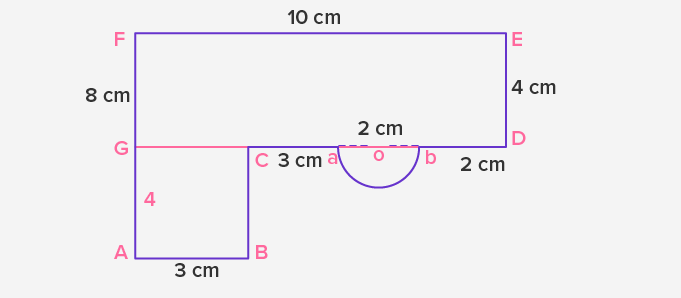
The following figure is an irregular shape with 8 sides, including one curve. Determine the unknown quantities by the given dimensions for the sides. Decompose the figure into two rectangles and a semicircle.
The area of the shape ABCDEF is:
Area (ABCDEF) = Area (ABCG) + Area (GDEF) + Area (aob)
Area = (AB × AG) + (GD × DE) + (1⁄2 × π × ob2)
Area = (3 × 4) + (10 × 4) + (1⁄2 × 3.14 × 12)
Area = 12 + 40 + 1.57
Area = 53.57 cm2
Application
The estimation of area for irregular figures is an essential method for drawing maps, building architecture, and marking agricultural fields. We apply the concept in the cutting of fabrics as per the given design. In higher grades, the technique lays a basis for advanced topics such as calculating volume, drawing conic sections and figures with elliptical shapes.
| Fun Fact – Tangram polygons are ancient examples of geometric shapes and can create more than 6500 shapes. |

Recommended Games
Related Math Vocabulary
Recommended Worksheets
Practice Problems On Area of Irregular Shapes
Area of Irregular Shapes
A leaf was traced on a graph paper. It has 10 squares fully covered, 12 squares are covered more than half and 14 squares are covered less than half. What will be the area of the leaf?
The fully covered squares are counted as it is. More than half-covered squares are counted as 1 square each. Less than half-covered squares are counted as 0 each.
So we have $10 + (1 × 12) + (0 × 14) = 10 + 12 = 22$ square units.
What is the area of a field that is shaped like 2 rectangles with the following measurements: Rectangle 1: l = 5, w = 6 Rectangle 2: l = 8, w = 5
Area of Rectangle 1 = 5 × 6 = 30 sq.cm.
Area of Rectangle 2 = 8 × 5 = 40 sq.cm
Area of Field = Area of Rectangle 1 + Area of Rectangle 2
= 30 + 40 = 70 square cm.
To find the area of an irregular shape, we first break the irregular shape into common shapes. Then we find the area of each shape and ___ them.
To find the area of an irregular shape, we first break the shape into common shapes. Then we find the area of each shape and add them. For example, if an irregular polygon is made up of a square and a triangle, then: Area of irregular polygon = Area of Square + Area of Triangle.
What is the area of an irregular polygon made of 2 squares with the following measurements? Square 1: side = 5 cm Square 2: side = 3 cm
Area of Square 1 = 5 × 5 = 25 sq. cm.
Area of Square 2 = 3 × 3 = 9 sq. cm.
Area of Irregular polygon = Area of Square 1 + Area of Square 2 = 25 + 9 = 34 square cm.
Frequently Asked Questions On Area of Irregular Shapes
How do we find the area of irregular shapes?
An irregular shape can be decomposed into known polygons. The area of the irregular shape then is the sum of the area of each of these polygons. If the irregular shape has curved edges and decomposing the entire shape into known polygons is not possible, then estimating the area would be a better approach.
Is there any formula to find areas of irregular shapes?
No, there is no general formula to calculate the area of an irregular shape because the sides can be of varying lengths and curves.
Where do we need to find the area of irregular shapes in real life?
We need to find the area of irregular shapes for drawing maps, building architecture, and marking agricultural fields. We also need it for cutting fabrics according to a given design.
Is there any easy method to calculate the area of irregular shapes?
If an irregular shape can be drawn or traced on a grid paper, then counting the number of squares covering the entire shape will be the easiest way to find its area.




































