Improper Fraction to Mixed Number –  Conversion, Example, Facts, FAQs

What Is Improper Fraction to Mixed Number Conversion?

Improper fraction to mixed number conversion helps us express any given improper fraction in the form of a mixed number (or mixed fraction). 

Note that an improper fraction and mixed number basically mean the same thing, but the way of representation is different. Let’s see how. 

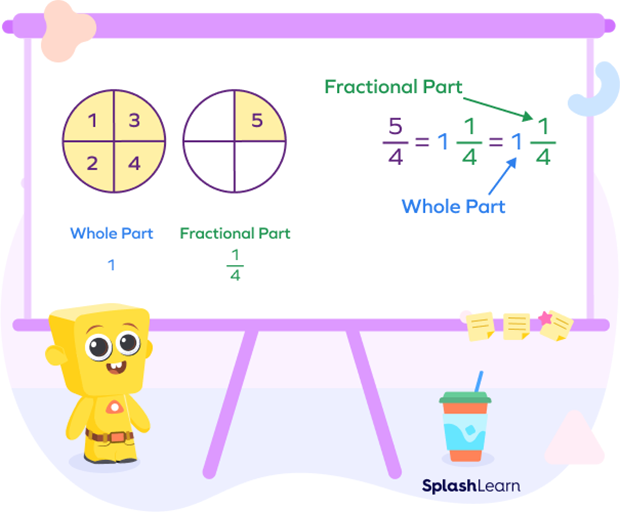
An improper fraction is a fraction whose numerator is greater than the denominator. Since the numerator > denominator, the value of an improper fraction is always greater than 1. 

Examples: $\frac{3}{2}, \frac{9}{4}, \frac{47}{12}$ 

A mixed fraction is a fraction which consists of a whole number and a proper fraction. Thus, a mixed number is always greater than 1. 

Examples: $1\frac{1}{2}, 2\frac{1}{4}, 3\frac{11}{12}$ 

So, how do we turn an improper fraction into a mixed number? Let’s find out!

How to Convert an Improper Fraction to a Mixed Number

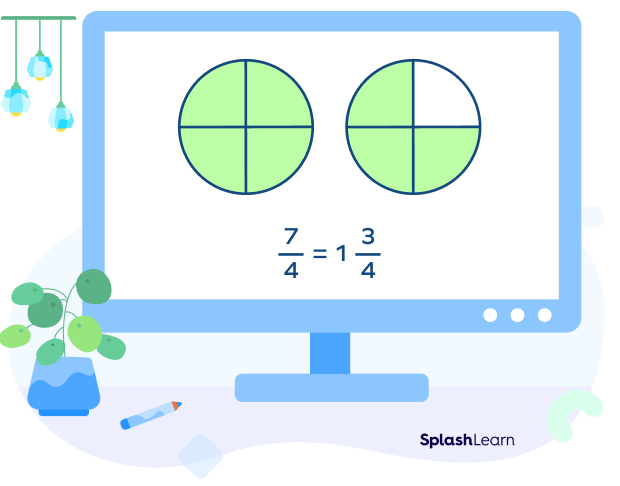
Let’s understand the steps with an example. Suppose we have to convert an improper fraction $\frac{7}{4}$ to a mixed number. If we visualize $\frac{7}{4}$, we get 

Step 1: Divide the numerator by the denominator. In this case, we get

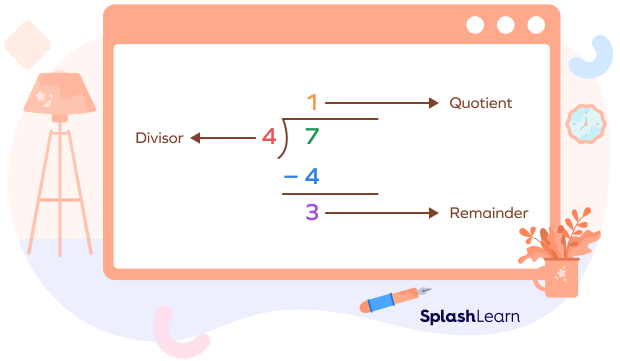
Step 2: Note down the quotient and remainder. The quotient acts as the whole number part of the mixed number. The remainder is the new numerator. The denominator stays the same.

In simple words, write the mixed number in the form

 $Quotient\frac{Remainder}{Divisor}$. 

In this case, we get $\frac{7}{4} = 1 R 3$

It means that quotient $= 1$ and remainder $= 3$

Thus, $\frac{7}{4} = 1\frac{3}{4}$

Converting an Improper Fraction To Mixed Number: Examples

Let’s discuss a few examples.

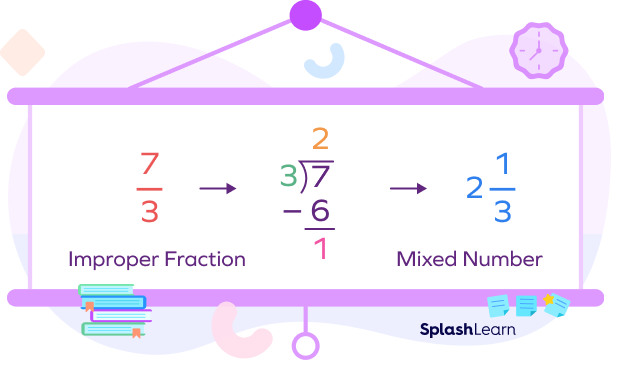
Example 1:$\frac{7}{3} = 2\frac{1}{3}$

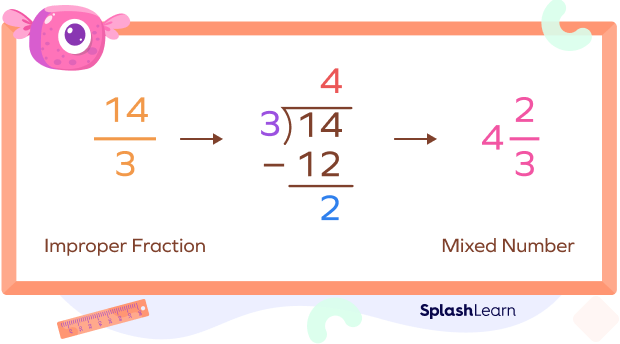
Example 2: $\frac{14}{3} = 4\frac{2}{3}$

Addition of Improper Fraction and Mixed Number

Addition of an improper fraction and a mixed number is quite easy. It can be done easily by converting the mixed number into an improper fraction. We will discuss two cases here.

Same Denominators

If the denominators of two fractions are the same, they are called the like fractions. In case the denominators are the same, then the numerators can be added while the denominator remains the same. 

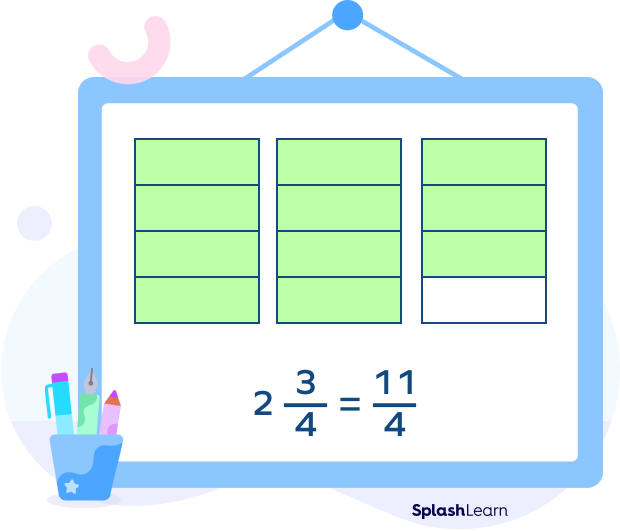
Suppose we have to add $2\frac{1}{4}$ to $\frac{11}{4}$. 

$2\frac{1}{4} = \frac{(2 \times 4) + 1}{4} = \frac{9}{4}$

$\frac{9}{4} + \frac{11}{4} = \frac{20}{4} = 5$

Different Denominators

If the denominators of two fractions are different, they are called unlike fractions. Here, we first change them to a common denominator using the LCM method.

Suppose we have to add $2\frac{1}{2}$ to $\frac{7}{3}$.

$2\frac{1}{2} = \frac{5}{2}$

LCM $(2, 3) = 6$

$\frac{5 \times 3}{2 \times 3} = \frac{15}{6}$

$\frac{7 \times 2}{3 \times 2} = \frac{14}{6}$

$2\frac{1}{2} + \frac{7}{3} = \frac{15}{6} + \frac{14}{6}$

    $= \frac{15 + 14}{6}$

    $= \frac{29}{6}$

    $= 4\frac{5}{6}$

Facts on Improper Fraction to Mixed Number Conversion

Conclusion

In this article, we learned how to convert improper fractions into mixed numbers. Let’s solve a few examples and practice problems for revision.

Solved Examples on Improper Fraction to Mixed Number Conversion

1. Convert improper fraction into a mixed number: 175 

Solution:

Divide 17 by 5.

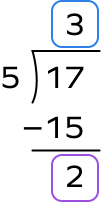
Note down the quotient and remainder. 

Quotient $= 3$

Remainder $= 2$

The quotient becomes the whole number part of the mixed number. The remainder acts as the new numerator. The denominator stays the same. 

$\frac{17}{5} = 3\frac{2}{5}$

2. Convert improper fraction into a mixed number: $\frac{121}{10}$

Solution: 

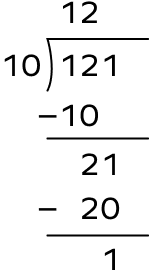
Quotient $= 12$ is to be written the new whole part of the mixed number.

Remainder $= 1$ is the new numerator. 

Denominator $= 10$ stays the same.

Thus, $\frac{121}{10} = 12\frac{1}{10}$

3. Convert improper fraction into a mixed number: $\frac{10}{3}$.

Solution: 

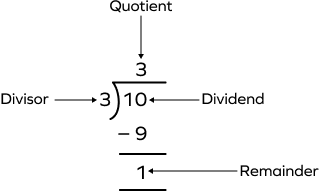
Quotient $= 3$

Remainder $= 1$

$\frac{10}{3} = 3\frac{1}{3}$

4. Add a mixed number and an improper fraction: $2\frac{3}{5} + \frac{21}{5}$. 

Solution:

To add $2\frac{3}{5}$ and $\frac{21}{5}$, we first need to convert improper fraction into a mixed number.

$2\frac{3}{5} = \frac{(5 \times 2) + 3}{5} = \frac{13}{5}$ 

$2\frac{3}{5} + \frac{22}{5} = \frac{13}{5} + \frac{21}{5} = \frac{13 + 21}{5} = \frac{34}{5}$

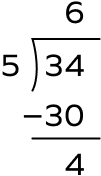
Quotient $= 6$

Remainder $= 4$

Thus, $\frac{34}{5} = 6\frac{4}{5}$

5. Convert improper fraction into a mixed number: $\frac{15}{7}$ 

Solution:

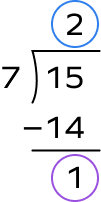
Quotient $= 2$

Remainder $= 1$

$\frac{15}{7} = 2\frac{1}{6}$

Practice Problems on Improper Fraction to Mixed Number Conversion

Frequently Asked Questions on Improper Fraction to Mixed Number Conversion