Mixed Number to Decimal Conversion – Definition, Examples, FAQs

What Is Mixed Number to Decimal Conversion?

Mixed number to decimal conversion is used to express a given mixed number (mixed fraction) in the form of a decimal. It is very simple to write a mixed number as a decimal. 

What is a mixed number?

A mixed number consists of a whole number and a proper fraction. It is also popularly known as a mixed fraction. 

Example: $2\frac{1}{4}$ 

What are decimals?

A decimal consists of a whole number part and a fractional part separated by a decimal point. The digits placed to the right of a decimal point together define the fractional part.

Example: 2.25

We know that to convert a fraction into a decimal, we divide the numerator by the denominator. Here, the only difference is that we have to convert a fraction with a whole number to a decimal. 

How to Convert a Mixed Number to a Decimal

Let’s understand how to write mixed numbers as decimals. There are two ways to transform a mixed fraction into a decimal.

i) Convert the mixed number into an improper fraction. Next, convert the improper fraction into a decimal by dividing the numerator by the denominator. 

ii) Focus on the fractional part of the mixed number. Convert it into a decimal. Add the whole number to the decimal obtained.

Thus, to convert mixed numbers or mixed fractions to decimals, it is essential to know the following conversions:

• How to convert a mixed number into an improper fraction
• How to change a fraction into a decimal number

Converting Mixed Numbers to Decimals: Methods with Steps

As mentioned earlier, there are two methods to convert mixed fractions into decimals. Let’s explore the steps for each in detail. You should choose whichever method suits you or the method specifically mentioned in the question.

Method 1: Mixed Number Improper Fraction Decimal

Step 1: Convert the mixed number into an improper fraction.

Step 2: Convert the improper fraction into a decimal.

Example: Write the mixed number as a decimal: $3\frac{5}{8}$

Mixed number to improper fraction:  $3\frac{5}{8} = \frac{(8 \times 3) + 5}{8} = \frac{29}{8}$

Improper fraction to decimal: Now, we will convert the improper fraction $\frac{29}{8}$ into a decimal. Divide the numerator by the denominator.

$29 \div 8 = 3.625$

Therefore, we get the decimal form 3.625 equivalent to the mixed number $3\frac{5}{8}$.

Method 2: Converting the Fractional Part into a Decimal

Step 1: Convert the fraction part of the given mixed fraction or number into a decimal form. 

Step 2: Add the whole number of the mixed fraction to the calculated decimal form in step 1.

Note that in method 2, initially, we do not touch the whole number part. First, we have to convert the fraction part of the given mixed number to decimals.

Example: Write the mixed number as a decimal: $3\frac{5}{8}$.

In the mixed number $3\frac{5}{8}$, the whole number part is 3 and the fractional part is $\frac{5}{8}$. Let’s convert the fraction $\frac{5}{8}$ into the decimal form by dividing 5 by 8.

$5 \div 8 = 0.625$.

Now, add the whole number part to the decimal part.

$0.625 + 3 = 3.625$

Hence, both the methods give the same answer.

$3\frac{5}{8} = 3.625$ 

Isn’t it fun to learn how to write mixed numbers as decimals? Now, let’s move on to learn the exact opposite of what we did. Let’s change decimals to mixed numbers.

Converting Decimals to Mixed Numbers (H2)

Conversion of a decimal to a mixed number is equally easy. All we need to do is reverse the concept that we used to convert a mixed number into its decimal form. We can follow these steps:

Step 1: Count the decimal places in a given number.

Step 2: Remove the decimal point.

Step 3: Divide the obtained number by a power of 10 according to the number of digits placed after the decimal point.

For example, a number with two decimal places will be divided by 100 (the number of zeros will increase or decrease according to the strength of decimal places).

Step. 4: Simplify and reduce to the lowest form.

Example: Convert 3.625 into a mixed number.

There are three digits after the decimal point. Thus, divide 3625 by $10^{3} = 1000$.

$3.625 = \frac{3625}{1000}$

$\Rightarrow 3.625 = \frac{29}{8}$ 

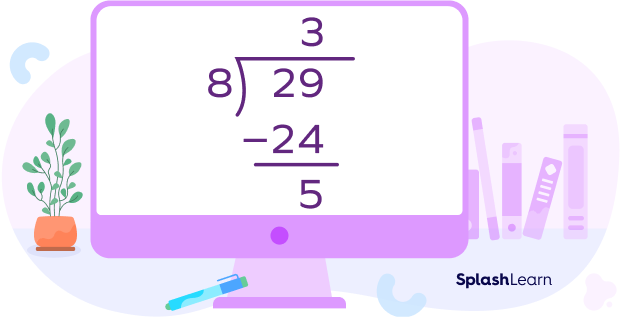
$\Rightarrow 3.625 = 3\frac{5}{8}$ is a mixed number.

Visualize Mixed Number to Decimal Conversion

The mixed number appears as a combination of a whole number and a fraction. Decimals also have a whole part and a fractional part. Thus, interconversion between mixed numbers and decimals is simple and pretty intuitive. 

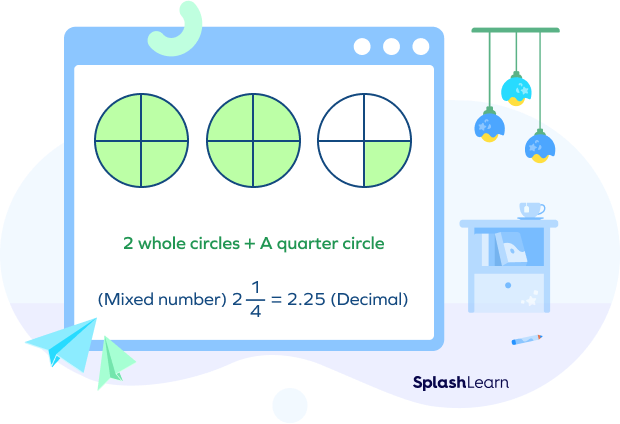
Consider the mixed number  $2\frac{1}{4}$. 

Whole number part $= 2$ and fractional part $= \frac{1}{4}$.

Thus, two whole circles plus a quarter of a circle are shaded. Note that a quarter can be written in the decimal form as 0.25.

Facts about Mixed Number to Decimal Conversion

Conclusion

In this article, we learned about mixed number to decimal conversion using two methods. Let’s solve a few examples based on this conversion for practice.

Solved Examples on Mixed Number to Decimal Conversion

1. Convert $6\frac{2}{3}$ into decimal form.

Solution: 

Converting the fraction $\frac{2}{3}$ to decimal, we get

$\frac{2}{3} = 2 \div 3 = 0.66$…

Adding the whole number 6 to the decimal 0.66…, we get

$6+ 0.66 = 6.66$…

Thus,  $6\frac{2}{3} = 6.66$..

2. Convert 248 into decimal form.

Solution: 

Convert the mixed fraction to improper fraction.

$2\frac{4}{8} = (8 \times 2) + 4 = \frac{20}{8}$

Now, write the improper fraction as a decimal.

$20 \div 8 = 2.5$

Thus, $2\frac{4}{8} = 2.5$

3. Lara needs 6.5 yards of a cloth for her design project. She already has $6\frac{3}{5}$ yards of material. Does she have enough cloth material?

Solution:

Lara has $6\frac{3}{5}$ yards of cloth material with her. Let’s convert it to decimal form so that it’s easier to compare with 6.5.

First, convert the fraction part of $6\frac{3}{5}$ into its decimal form.

$\frac{3}{5} = 3 \div 5 = 0.6$

Then, add the whole number to the decimal number.

$6 + 0.6 = 6.6$

Thus, Lara has 6.6 yards of cloth.

Since Lara requires 6.5 yards of fabric, 635 yards of fabric is enough for her project.

Practice Problems on Mixed Number to Decimal Conversion

Frequently Asked Questions on Mixed Number to Decimal Conversion