The perimeter of a rhombus is the total length of its outer boundary. It is measured in linear units, such as feet, inches, yards, etc.
Perimeter of a rhombus $= 4 \times side$
A rhombus is a quadrilateral (a four-sided polygon) with the following properties:
- All sides are equal.
- Opposite angles are congruent.
- Adjacent angles are supplementary.
- Opposite sides are parallel.
- The altitude is a distance at right angles between two parallel sides.
- The diagonals of a rhombus bisect each other at the right angles.
- Each diagonal bisects the vertex angle.
Its properties make it a unique and important geometric shape. Let’s explore the perimeter of rhombus in detail.
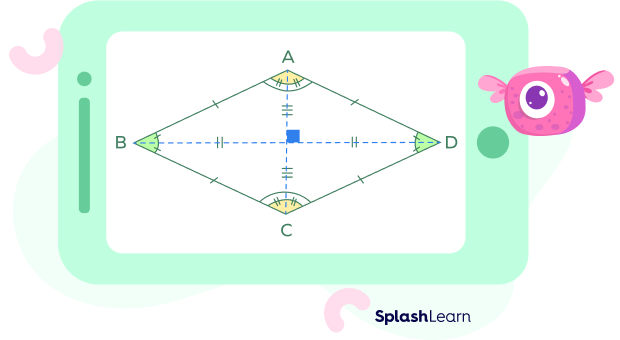
The image above shows a rhombus ABCD, along with its important properties.
So, what is the perimeter of the rhombus ABCD? How do you find the perimeter of a rhombus? Let’s discuss formulas and methods in detail.
Perimeter of a Rhombus: Formulas
Let’s discuss the formulas for the perimeter of a rhombus with two cases.
- When the side length is known
Perimeter of a rhombus with side “a” $= 4 \times a$
- When the length of the diagonals is known
Perimeter of a rhombus with diagonals p and $q = 2\sqrt{p^{2} + q^{2}}$
Recommended Games
How to Find the Perimeter of a Rhombus
To find the perimeter of a rhombus, first note down the known dimensions. Make sure that all the measurements are in the same unit.
If the side length of a rhombus is known, use the first formula $P = 4\times$ side length.
If the lengths of the two diagonals of a rhombus are known $(say\; d_{1}$ and $d_{2})$, use the formula $= 2\sqrt{d_{1}^{2} + d_{2}^{2}}$
Perimeter of a Rhombus Using the Side Lengths
The perimeter of a rhombus is defined as the total distance around the outline of the shape. It is the sum of the lengths of all four sides. Since all sides of a rhombus are equal, the formula for the perimeter is simply four times the length of one side.
Perimeter of a rhombus with side “x” $= x + x + x + x$
Perimeter $= 4\times $ Side Length $= 4x$
Example: Find the perimeter of a rhombus with a side length of 8 inches.
Perimeter $= 4\times$ Side Length
Perimeter $= 4 \times 8$ inches
Perimeter $= 32$ inches
So, the perimeter of the rhombus is 32 inches.
Perimeter of a Rhombus Using Diagonals
When the length of the diagonals of a rhombus is given, we first find the side length of the rhombus using the Pythagoras’ theorem.
The properties of rhombus we use here are
- A rhombus is divided into 4 congruent right triangles by its two diagonals.
- The diagonals bisect each other at right angles.
Let us consider a rhombus ABCD with diagonals p and q and with side length “a.”
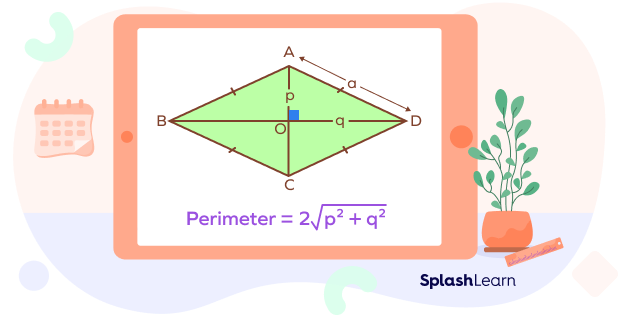
Consider the triangle AOD.
Since the diagonals bisect at right angles, we can write
AO $= \frac{p}{2}$ and OD $= \frac{q}{2}$.
On applying the Pythagoras’ theorem for triangle AOD, we get
$a^{2} = \frac{p^{2}}{4} + \frac{q^{2}}{4}$
$a = \sqrt{\frac{p^{2} + q{2}}{2}}$
Perimeter of a rhombus $= 4a =4 \times \sqrt{\frac{p^{2} + q^{2}}{2}} = 2\sqrt{p^{2} + q^{2}}$
Perimeter of a Rhombus Using One Diagonal and One Angle
Suppose that you know the length of one of the two diagonals and one interior angle. Now, to find the perimeter of the rhombus, you first need to find the length of the side using the different properties of a rhombus. Let’s understand this with an example.
Example: Find the perimeter of the rhombus ABCD given below.
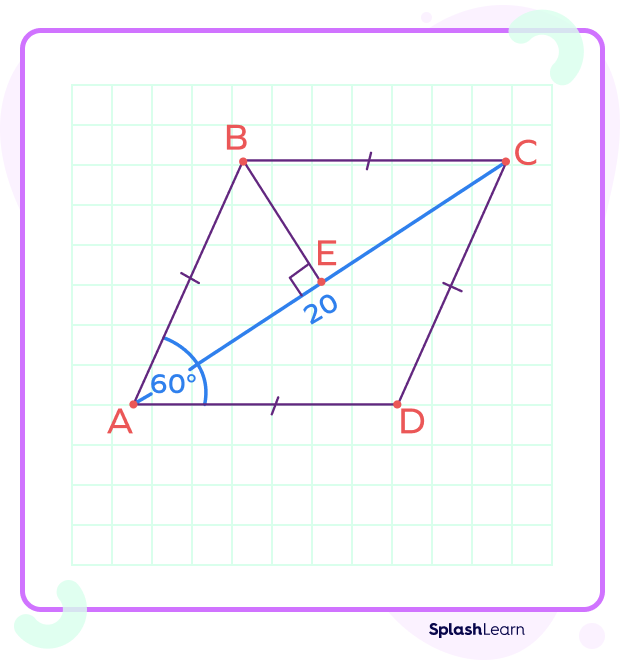
Given: $\angle A = 60^{\circ}$ and $AC = 20$
Each diagonal bisects the vertex angle.
Thus, $\angle BAE = \frac{1}{2} \angle BAD = 30^{\circ}$
The diagonals of a rhombus bisect each other at right angles.
Thus, $\angle AEB = 90^{\circ}$ and $AE = \frac{1}{2}\times AC = 10$
In triangle AEB, $cos(\angle BAE) = cos(30^{\circ})= \frac{\sqrt{3}}{2}$
Also, $cos(\angle BAE) = \frac{AE}{AB}$
Thus, $\frac{\sqrt{3}}{2} = \frac{10}{AB}$
$AB = \frac{20}{\sqrt{3}}$ …side of rhombus ABCD
Thus, perimeter of rhombus $ABCD = 4 \times side = 4 \times \frac{20}{\sqrt{3}} = \frac{80}{\sqrt{3}} \approx 46$ units
Conclusion
In this article, we learned how to find the perimeter of a rhombus and also the different methods to calculate the perimeter of a rhombus. Let’s use these concepts and move ahead to solve a few examples and practice problems.
Solved Examples on the Perimeter of a Rhombus
1. What is the perimeter of a rhombus with each side length equal to 10 inches?
Solution:
Side of rhombus $= a = 10$ inches
Perimeter of rhombus $= 4a = 4 \times 8 = 32$ inches
2. Find the side of a rhombus if the perimeter is 36 feet.
Solution:
Perimeter of a rhombus $= 36$ feet
Let the side of the rhombus be “a” feet.
$4a = 36$ feet
$a = \frac{36}{4} = 9$ feet
3. If the diagonals of the rhombus are 6 and 8 inches, then what is the perimeter of the rhombus?
Solution:
Let $p = 6$ inches and $q = 8$ inches
Perimeter of a rhombus with diagonals p and $q = 2\sqrt{p^{2} + q^{2}}$
Perimeter of the rhombus $= 2\sqrt{6^{2} + 8^{2}}$
$=2 \times 10$
$=20$ inches
4. ABCD is a rhombus with sides 15 inches. What is the perimeter of the rhombus ABCD?
Solution:
Side of rhombus $= a = 15$ inches
Perimeter of rhombus $= 4a = 4 \times 15 = 60$ inches
5. A field is in the shape of a rhombus with sides 13 feet. Find the length of the boundary of the field.
Solution:
Length of the boundary of the field = Perimeter of the rhombus
Side of rhombus shaped field $= a = 13$ feet
Perimeter of the field $= 4a = 4 \times 13 = 42$ feet
Length of the boundary of the field $= 42$ feet
Practice Problems on Perimeter of a Rhombus
Perimeter of a Rhombus - Definition, Formula, Examples, Facts, FAQs
If the perimeter of a rhombus is 48 in, then what is the length of each side?
Perimeter of a rhombus$= 48$ inches
Let the side of the rhombus be “a” inches.
$4a = 48$
$a = \frac{48}{4} = 12$ inches
What is the perimeter of the square if the side length is 18 feet?
side of rhombus, i.e., $a = 18$ feet
Perimeter of rhombus $= 4a = 4 \times 18 = 72$ feet
The formula for the perimeter of a rhombus with side “a” is
Perimeter of rhombus with side “a” $= 4a$
If the diagonals of the rhombus are 21 inches and 20 inches, then what will be the perimeter of the rhombus?
Perimeter of the rhombus $= 2\sqrt{p^{2} + q^{2}} =2\sqrt{21^{2} + 20^{2}} = 2\sqrt{841} = 2 \times 29 = 58$ in
If the perimeter of a rhombus is 68 inches and the length of one diagonal is 16 inches, then what is the length of the other diagonal?
Perimeter of the rhombus $= 2\sqrt{p^{2} + q^{2}}$
Let $p = 16$ inches
$68 = 2\sqrt{p^{2} + q^{2}}$
$34 = \sqrt{16^{2} + q^{2}}$
$1156 = 256 + q^{2}$
$q^{2} = 1156\;-\;256 = 900$
$q = 30$ inches
Frequently Asked Questions on Perimeter of a Rhombus
What is the difference between area and perimeter?
The area of a 2D shape is the region bounded by the shape, whereas the perimeter is the length of the boundary of the shape.
What is the perimeter of the square?
Perimeter of a square $= 4 \times$ side of the square
What is the area of a rhombus?
Area of rhombus when diagonals are given $= \frac{1}{2} \times d_{1} \times d_{2}$
Area of rhombus when base and height is given $= b \times h$
Are all rhombuses squares?
All squares are rhombuses, but all rhombuses are not squares. If you have a rhombus with four equal interior angles, you have a square. A square is a special case of a rhombus, because it has four equal-length sides and goes above and beyond that to also have four right angles.
Are all four angles of a rhombus equal?
No, the opposite angles of a rhombus are equal and the adjacent angles are supplementary.


























