What Are the Properties of Integers?
Properties of integers in mathematics are certain rules that can be applied to simplify calculations when we perform arithmetic operations on them.
The set of integers are represented by the symbol ℤ.
ℤ $= \left\{…,-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5,…\right\}$
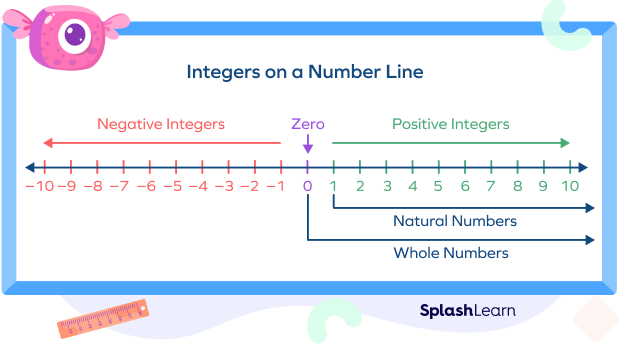
The basic operation of addition, subtraction, multiplication, and division give rise to five main types of properties in integers:
1. Closure Property
2. Associative Property
3. Commutative Property
4. Distributive Property
5. Identity Property
Properties of Integers
Here’s a chart of properties of integers that gives an overview of each property.
| Closure Property | $a + b \in$ ℤ $a \;-\; b \in$ ℤ $a \times b \in$ ℤ for any two integers a and b |
| Commutative Property | $a + b = b +a$ $a \times b = b \times a$ for any two integers a and b |
| Associative Property | $(a + b) + c = a + (b + c)$ $(a \times b) \times c = a \times (b \times c)$ for integers a, b, and c |
| Distributive Property | $a \times (b + c) = (a \times b) + (a \times c)$ $a \times (b\;-\;c) =(a \times b)\;-\;(a \times c)$ for integers a, b, and c |
| Identity Property | $a + 0 = a a \times 1 = 1 \times a = a$\ for any integer a |
Let’s study all properties of integers in detail.
Recommended Worksheets
Closure Property of Integers
The closure property of integers states that the addition, subtraction, or multiplication of integers always results in an integer.
For any two integers a and b, we have
- $a + b =$ integer
- $a \;-\; b =$ integer
- $a \times b =$ integer
Examples:
- $-\;5 + 4 = -\;3$
- $8\;-\;5 = 3$
- $2 \times 3 = 6$
However, the closure property of integers does not work for the division of integers because the division of two integers may not be an integer.
For example: $15 \div 2 = 7.5$
Associative Property of Integers
According to the associative property of integers, if we add three or more integers, the result is not affected by the way we group the integers. Similarly, the product of three or more integers does not depend on how we group them.
Associative property of integers is true only for the addition and multiplication but not for division and subtraction.
For any three integers a, b, and c, we have
- Associative property of addition: $a + (b + c) = (a + b) + c$
- Associative property of multiplication: $a \times (b \times c) = (a \times b) \times c$
However,
Examples:
| Operation | Result | Examples |
|---|---|---|
| Addition of integers | Associative property is satisfied. | $1 + (2 + 3) = 6$ $(1 + 2) + 3 = 6$ |
| Multiplication of integers | Associative property is satisfied. | $4 \times (2 \times 3) = 24$ $(4 \times 2) \times 3 = 24$ |
| Subtraction of integers | Associative property is not satisfied. | $1 \;-\; (2 \;-\; 3) = 2$ $(1\;-\;2)\;-\;3 = \;-4$ |
| Division of integers | Associative property is not satisfied. | $8\div (4 \div 2) = 4$ $(8 \div 4) \div 2 = 1$ |
Commutative Property of Integers
The commutative property states that changing the order of integers in addition and multiplication does not change the result of the operation.
Interestingly, this property is true for only the addition and multiplication and not for division and subtraction.
For two integers a and b, we have
- Commutative property of addition: $a + b = b + a$
- Commutative property of multiplication: $a \times b = b \times a$
Examples:
| Operation | Result | Example |
|---|---|---|
| Addition of integers | Commutative property is satisfied. | $1 + 2 = 3 = 2 + 1$ |
| Multiplication of integers | Commutative property is satisfied. | $1 \times 2 = 3 = 2 \times 1$ |
| Subtraction of integers | Commutative property is not satisfied. | $1\;-\;2 = 1\;-\;2$ |
| Division of integers | Commutative property is not satisfied. | $1\;-\;2 = 1\;-\;2$ |
Distributive Property of Integers
The distributive property states that the multiplication of integers can be distributed over addition and subtraction to make the calculation easier.
So, for any three integers a, b, and c, we have
- Distributive property of multiplication over addition: $a \times (b + c) =(a \times b) + (a \times c)$
- Distributive property of multiplication over subtraction: $a \times (b\;-\;c) = (a \times b)\;-\;(a \times c)$
Example:
- $5 \times (4 + 3) = (5 \times 4) + (5 \times 3) = 35$
- $\;-\; 2 \times (6 \;-\; 1) = (\;-\; 2 \times 6) + (\;-\; 2 \;-\;1) = \;-\; 10$
Identity Property of Integers
The identity property of an integer states that any integer added to zero will result in the same integer. Also, any integer multiplied by one will give the same integer.
0 is the additive identity of integers.
1 is the multiplicative identity of integers.
So, for any integer a, we have
- $a + 0 = 0 + a = a$
- $a \times 1 = 1 \times a = a$
Example:
- $5 + 0 = 0 + 5 = 5$
- $5 \times 1 = 1 \times 5 = 5$
Facts about Properties of Integers
- The use of the letter “ℤ” to denote the set of integers comes from the German word “Zahlen” which means “numbers.”
- There are an infinite number of integers.
- 0 is an integer that is neither positive nor negative.
- Every integer has an additive inverse. The additive inverse of an integer a is -a.
- Properties of multiplication of integers: Multiplication of integers follows closure property, commutative property, associative property, distributive property, and identity property.
- Rules for multiplying integers with different signs:
Positive integer $\times$ Positive integer $=$ Positive integer
Positive integer $\times$ Negative integer $=$ Negative integer
Negative integer $\times$ Negative integer $=$ Positive integer
Conclusion
In this article, we have learned the various properties of integers. These properties of integers can be used to speed up and simplify a number of operations on integers. Now, let’s solve some examples and practice problems to understand the concept better.
Solved Examples on Properties of Integers
1. Identify the correct properties of integers used in the following equations:
a) $a + (b + c) = (a + b) + c$
b) $a + 0 = 0 + a = a$
Solution:
a) $a + (b + c) = (a + b) + c$ shows the associative property of integers.
It shows that the addition of three or more integers does not depend on how we group them.
b) $a + 0 = 0 + a = a$ shows the identity property of integers
Addition of any integer and 0 is the integer itself.
2. Evaluate the expression: $(10 \times 5) + (10 \times 5)$ using the properties of integers.
Solution:
The given expression is $(10 \times 5) + (10 \times 4)$.
It can be solved by using the distributive property of integers, which states that,
For any three integers a, b, and c:
$(a \times b) + (a \times c) = a \times (b + c)$
$(10 \times 5) + (10 \times 4) = 10 \times (5 + 4)$
$= 10 \times 9$
$= 90$
Therefore, $(10 \times 5) + (10 \times 4) = 90$
3. If $a = \;-\;35$, $b = 10$ units and $c = \;-\;5$, verify that:
(i) $a + (b + c) = (a + b) + c$
(ii) $a \times (b + c) = (a \times b) + (a \times c)$
Solution:
Given that $a = \;-\;35\;, b = 10\;, c = \;-\;5$
(i) $a + (b + c) = (a + b) + c$
L.H.S. $= a + (b + c) = (\;-\;35) + \left[10 + (\;-\;5)\right] = (\;-\;35) + 5 = \;-\;30$
R.H.S. $= (a + b) + c = \left[(\;-\;35) + 10\right] + (\;-\;5) = (\;-\;25) + (\;-\;5) = \;-\;(25 + 5) = \;-\;30$
Thus, L.H.S. = R.H.S.
Hence, verified.
(ii) $a \times (b + c) = (a \times b) + (a \times c)$
L.H.S. $= a(b + c)= (\;-\;35) \left[10 + (\;-\;5)\right] = (\;-\;35) 5 = \;-\;175$
R.H.S. $= (a \times b) + (a \times c) = (\;-\;35) \times 10 + (\;-\;35) \times (\;-\;5) = \;-\;350 + 175 = \;-\;175$
Thus, L.H.S. $=$ R.H.S.
4. State whether the following statements are true or false.
a) Closure property holds true for addition, subtraction and multiplication of integers.
b) The product of two negative integers is a negative integer.
c) According to commutative property of multiplication: $a \times (b \times c) = (a \times b) \times c$
Solution:
a) Closure property holds true for addition, subtraction and multiplication of integers.
True.
Closure property holds true for addition, subtraction and multiplication of integers. It fails for division of integers.
b) The product of two negative integers is a negative integer.
False.
The product of two negative integers is a positive integer.
c) According to commutative property of multiplication: $a \times (b \times c) = (a \times b) \times c$
False.
The commutative property of multiplication states that the order of integers in multiplication operation does not change the result of the operation.
Commutative property of multiplication: $a \times b = b \times a$
Practice Problems on Properties of Integers
Properties of Integers – Definition, Examples, Facts, FAQs
$8 + (3 + 4) = (8 + 3) + 4$ is an example of __________.
According to the associative property, for any three integers a, b, and c, we have $a + (b + c) = (a + b) + c$
$3(a + 4) = 3a + 12$ is an example of __________.
According to distributive property of multiplication over addition, for any three integers a, b, and c, we have $a \times (b + c) = (a \times b) + (a \times c)$
The _______________ property of addition states that any integer plus zero equals the same number.
The identity property of integers states that any integer added to zero will result in the same integer. So, for any integer a, $a + 0 = 0 + a = a$
The ______________ property states that changing the position of integers during addition and multiplication does not change the result of the operation.
The commutative property states that changing the position of integers during addition and multiplication does not change the result of the operation.
So, for two integers a and b:
$a + b = b + a$ and $a \times b = b \times a$
The __________ of integers doesn't follow the closure property.
The closure property states that the addition, subtraction, or multiplication of integers results in an integer. Division of integers doesn’t follow the closure property, i.e., the quotient of any two integers a and b, may or may not be an integer.
Frequently Asked Questions on Properties of Integers
Is 0 an integer?
Yes, 0 is an integer. According to the definition, integers are the numbers that include whole numbers and negative natural numbers. It is a number without any fractional part, and zero has no fractional part. However, 0 is neither positive nor negative.
Are integers real numbers?
Yes. Integers are real numbers. The set of integers form a subset of the set of integers.
What are perfect numbers?
Perfect number is a positive integer that is equal to the sum of its proper divisors. The smallest perfect number is 6. 6 has divisors 1, 2 and 3 (excluding itself), and $1 + 2 + 3 = 6$, so 6 is a perfect number. Other perfect numbers are 28, 496, and 8,128.
Is an integer always a whole number?
No, each integer is not a whole number. However, each whole number is an integer.
Set of whole numbers $= \left\{ 0, 1, 2, 3, 4, 5,…\right)$
Set of Integers $= \left\{………, \;-\;4, \;-\;3, \;-\;2, \;-\;1, 0, 1, 2, 3, 4, …\right\}$So, all whole numbers are integers, but not all integers are whole numbers. For example, -6 is an integer but not a whole number.
Are all integers natural numbers?
No, all integers are not natural numbers.
Natural numbers $= \left\{1, 2, 3,…\right\}$
Integers $= \left\{…− 3,− 2,− 1,0,1,2,3,…\right\}$
There are many integers that are not natural numbers (negatives and 0).
For example, −1 is an integer, but not a natural number. So, not all integers are natural numbers.
What are properties of addition and subtraction of integers?
The addition of integers follows the closure, commutative, associative, distributive, and identity property. The subtraction of integers follows the closure property. Also, integers follow distributive property over subtraction.

















