What Is the Volume of a Cuboid?
The volume of a cuboid is the amount of space occupied by the cuboid. It is calculated by multiplying the length, width, and height of the cuboid.
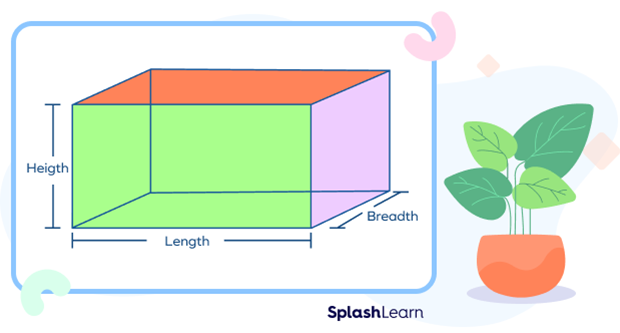
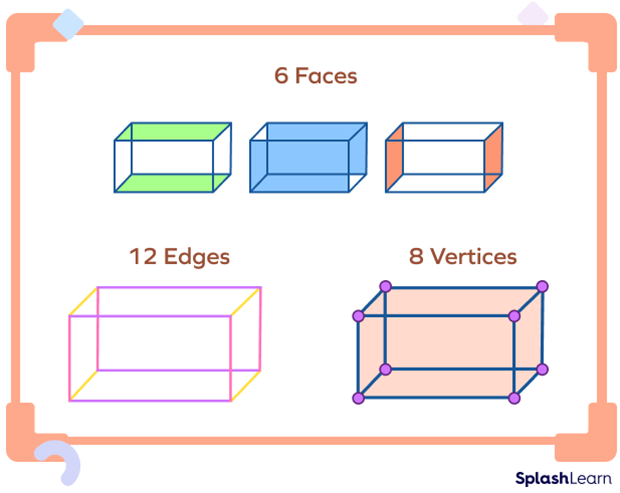
In geometry, a cuboid is a geometric solid with 6 faces, 12 edges, and 8 vertices.. The opposite faces of every cuboid are equal.
What do you mean by the volume of a cuboid? Just like area denotes the space occupied by an object on a 2D plane, the volume represents the space occupied by a solid in the 3D space. A cuboid is a three-dimensional solid. The total 3D space occupied by a cuboid is its volume.
A common real-life example of the volume of a cuboid is the amount of water that completely fills a cuboid-shaped aquarium.
Recommended Games
Volume of a Cuboid Formula
The volume of cuboid is a product of its length, breadth, and height.
The volume of a cuboid formula is written as
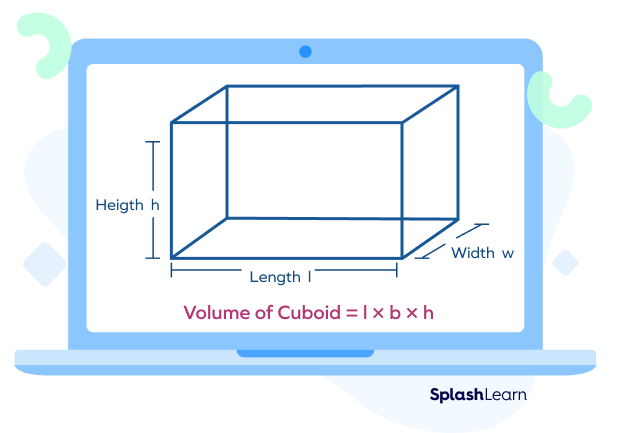
Volume of a cuboid $=$ length $×$ breadth $×$ height
Volume of a cuboid $= l \times b \times h$
Volume is measured in cubic units.
How to Calculate the Volume of a Cuboid
Step 1: Note down the dimensions of the given cuboid as $l = length,\; b = breadth,$ and $h = height$.
Step 2: Check whether they are all in the same unit or not. If we come across length, breadth, or height in different units, convert them into the same unit.
Step 3: Substitute the values l, b, and h in the volume formula $V = l \times b \times h$.
The resultant value will be the volume of a cuboid. It will be written with cubic units.
Volume of a Cuboid Prism
Cuboid prism or rectangular prism are just other names for a cuboid. A cuboid prism has a rectangular cross-section. It is called a right prism when the angles between its sides (lateral faces) and the base are right angles. Its top surface and the corresponding bottom will be identical.
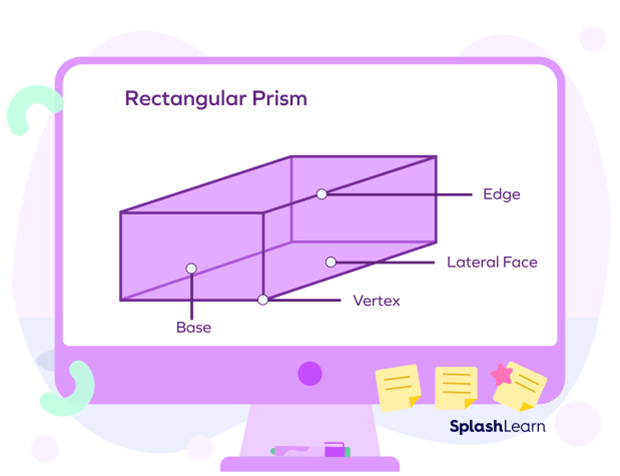
Therefore, using the same volume of cuboid formula, we can calculate the volume of a cuboid prism:
Volume of a cuboid prism $= l \times b \times h$ (cubic units)
If $l = b = h$, a cuboid becomes a cube. Its volume is given by $(side)^{3}$.
Volume of cube and cuboid are both expressed in $unit^{3}$.
Derivation of the Volume of a Cuboid
Interestingly, we can also calculate the volume of cuboid if we know its base area and height. Suppose the area of the cuboid’s rectangular face is A and the height of the cuboid is “h.”
Since volume is the space occupied, the mathematical expression will be as follows
Volume of a rectangular prism $=$ Base area $\times$ Height
$V = A \times h$ ————— (i)
As we know that the area of a rectangular surface can be calculated using the following formula:
$Area = length \times breadth$
$A = l \times b$ —————- (ii)
Substituting equation (ii) in equation (i), we get the following:
$V = A \times h$
$V = (l \times b) \times h$
Thus, we get the formula of a cuboid as follows:
$V = l \times b \times h$
Volume of Cuboid Using Unit Cubes
A unit cube is a cube whose each side is 1 unit. The volume of a cuboid can also be defined as the number of unit cubes that fit perfectly into the cuboid.
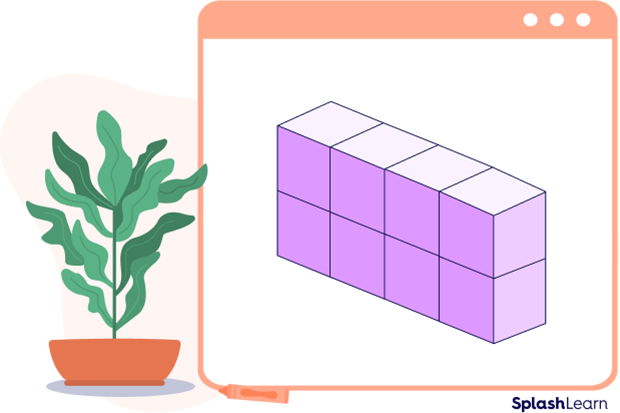
You can see that 8 unit cubes perfectly fit into the given cuboid.
Thus, volume of cuboid $= 8$ cubic units
Facts about Volume of Cuboid
- Cuboid is also known as a rectangular prism, rectangular box, rectangular parallelepiped, or a rectangular brick!
- Total Surface Area of Cuboid $= 2(lb + bh + hl)$
Conclusion
In this article, we learned how to find the volume of a cuboid, its formula, derivation, and examples. Now, we will solve a few examples and practice problems for revision.
Solved Examples of Volume of a Cuboid
1. What is the volume of the given cuboid?

Solution:
$l = 6$ inches
$b = 2$ inches
$h = 4$ inches
Volume of cuboid $= l \times b \times h$
Volume of cuboid $= 6 \times 4 \times 2$
Volume of cuboid $= 48\; inches^{3}$
2. The dimensions of the cuboid-shaped aquarium are: $h = 5$ inches, $l = 10$ inches, and $b = 8$ inches. What is the volume of the cuboid?

Solution:
$l = 10$ inches
$b = 8$ inches
$h = 5$ inches
Volume of cuboid $= l \times b \times h$
Volume of cuboid $= 10 \times 8 \times 5$
Volume of cuboid $= 400\; inches^{3}$
3. Find the length of the cuboid, if its volume is $24\; inches^{3}$. Given: breadth $= 6$ inches and height $= 2$ inches.
Solution:
Let the length of the cuboid be l.
Volume of cuboid $= l \times b \times h$
$24 = l \times 6 \times 2$
$24 = l \times 12$
$2412 = l$
$l = 2$ in
Therefore, the length of the cuboid is 2 inches.
Practice Problems for Volume of a Cuboid
Volume of Cuboid - Definition, Formula, Derivation, Examples, FAQs
What is the volume of the given cuboid?

Using the volume of cuboid formula, we will find the product of 10, 5, and 2 feet.
$V = l \times b \times h = 10 \times 2 \times 5 = 100 feet^{3}$.
A cuboid-shaped swimming pool is 20 feet long, 10 feet deep, and 8 feet wide. What is the volume of the swimming pool?
Using the volume of cuboid formula, we will find the product of 20, 10, and 8 feet.
$V = l \times b \times h = 20 \times 10 \times 8 = 1600\; feet^{3}$.
The formula to find the volume of a cuboid with length l, breadth b, and height h is ___
The volume of the cuboid formula is $l \times b \times h$.
What is the volume of the given rectangular prism?

Using the volume of cuboid formula, we will find the product of 8, 2, and 5 feet.
$V = l \times b \times h = 8 \times 2 \times 5 = 80\; feet^{3}$.
Frequently Asked Questions about Volume of Cuboid
What is the volume of a cube formula?
Since all sides of a cube are the same, the volume of a cube is equal to the cube of its side. Mathematically, $V = side^{3}$.
How to convert the volume of a cuboid in $inch^{3}$ to $feet^{3}$?
To convert a given volume in $inch^{3}$, we will divide the volume value by 1728 to get its $feet^{3}$ equivalent.
How will the volume of a cuboid change when we double the length of its side?
As the volume of cuboid $= length \times width \times height$, we will double the length.
So, $2l \times b \times h = 2$ volume.
Thus, the volume of the cuboid will be doubled when we double the length of its side.
























