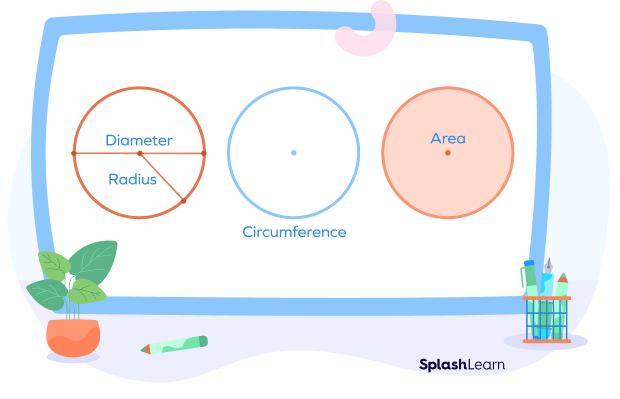
What Is the Area of a Circle?
The area of a circle is the region occupied by the circle within its boundary (circumference) in a 2D plane.
If the radius of a circle is r, the area is defined as A = πr2, where is a mathematical constant with approximate value of 3.14 or $\frac{22}{7}$.
Area of a circle is measured in square units.
Recommended Games
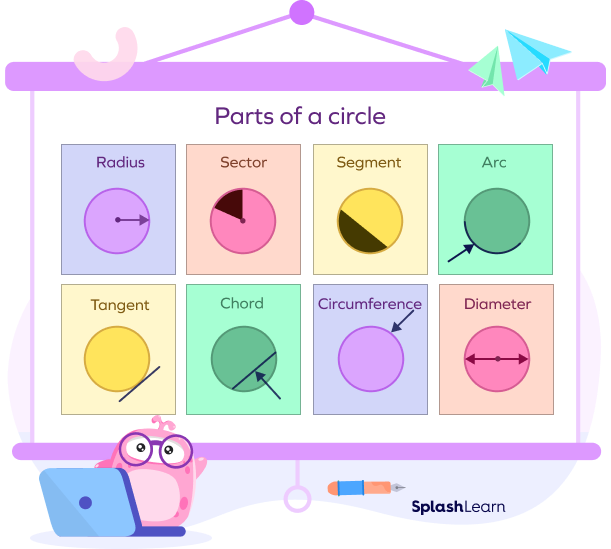
Parts of a Circle
A circle is a two-dimensional closed geometric shape that is a collection of all points which are at a fixed distance from a fixed point (center). This fixed distance is called the radius of the circle.
Let’s learn about different parts of a circle. It will help us in understanding the different formulas used to calculate the area of a circle.
| Part | Definition |
|---|---|
| Center | The fixed point at the middle that is equidistant from all the points from every point on the boundary of the circle. |
| Radius | The fixed distance from the center to any point on the circumference (boundary) of the circle. All radii (plural) of a circle are equal. |
| Diameter | A straight line that connects any two points on the circumference while passing through the center of the circle. |
| Circumference | The length of the boundary of a circle. |
| Chord | A line segment that connects any two points on the circumference of a circle. |
| Tangent | A straight line that passes by touching the circumference at one point. |
| Arc | A part of the circle’s circumference. |
| Segment | A region enclosed by an arc and a chord. |
| Sector | A region enclosed by 2 radii and an arc. |
Recommended Worksheets
Area of Circle Formulas
| Description | Formula |
|---|---|
| Area of a circle using radius | A = πr2 |
| Area of a circle using diameter | A $= \frac{\pi}{4} d^{2}$ |
| Area of a circle using circumference | A $= \frac{C^{2}}{4\pi}$ |
How to Find the Area of a Circle
Let’s discuss methods to find the area of a circle based on the information available.
- How to Find the Area of a Circle with Radius
The formula for the area of a circle (A) using its radius r is as follows:
A = πr2
Example: A circle has a radius of 5 inches. Find the area of the circle.
A = πr2
A = 3.14 × (5 inches)2
A = 3.14 × 25 inch2
A = 78.5 inch2
- How to Find the Area of a Circle with Diameter
We know that A = πr2 and r $= \frac{d}{2}$
The formula for the area of a circle (A) using its diameter (d) as follows:
A $= \frac{\pi}{4} d^{2}$
Example: A circle has a diameter of 10 inches. Find the area of the circle.
A $= \frac{\pi}{4} d^{2}$
A $= \frac{\pi}{4} \times $(10 inches)2
A $= (\frac{3.14159}{4}) \times 100$ inch2
A $= 78.54$ inch2
- How to Find the Area of a Circle with Circumference
Circumference = C = 2πr
Thus, r $= \frac{C}{2\pi}$
Substitute this value in the formula A = πr2.
A $= \pi (\frac{C}{2\pi})^{2}$
A $= \frac{C^{2}}{4\pi}$
Example: A circle has a circumference of 31.42 units. Find the area of the circle.
A $= \frac{C^{2}}{4\pi}$
A $= \frac{(31.42)^{2}}{4 \times 3.14}$
A = 78.6 inch2
Derivation of Area of a Circle Formula
You can visualize and derive the area of a circle by the following two methods:
- Derivation of the area of a circle formula using the area of a rectangle
The figure shows a circle divided into 16 equal sectors of equal areas. If the sectors are cut out from the circle and placed as a parallelogram-shaped figure, the area of the circle will be equal to the area of this figure.
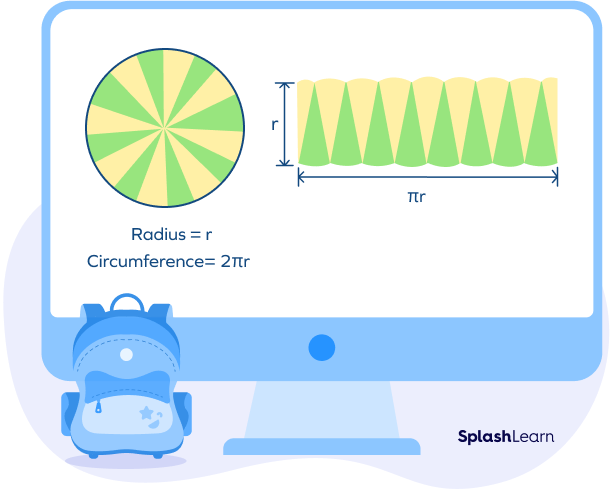
The pink-colored sectors will cover half of the circle and thus have half the circumference. The blue-colored sectors will cover the other half.
Radius = r
Circumference = 2πr
Circumference of Pink Sectors $= \frac{1}{2} \times 2\pi r = \pi r$
Circumference of Blue Sectors = πr
We can see that the parallelogram-like shape will appear like a rectangle if the number of sectors is increased.
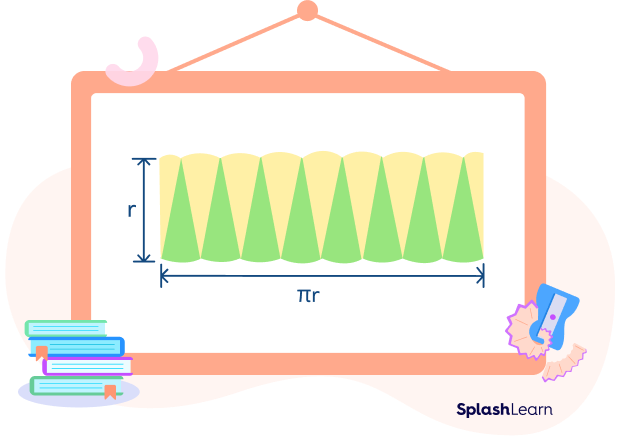
Length of the rectangle = πr
Breadth = r
Area of rectangle = l × b
Putting the values from the figure into the formula
A = πr × r
A = πr2
Area of a circle = πr2
- Derivation of the area of a circle formula using the area of a triangle
The figure below shows concentric circles throughout the radius. Imagine that the circle is cut along a radius and opened up to form a shape that resembles a triangle.
The circumference of a circle will become the base of the triangle, and the radius will become its height.
Circumference = 2πr
Radius = r = Height of the Triangle
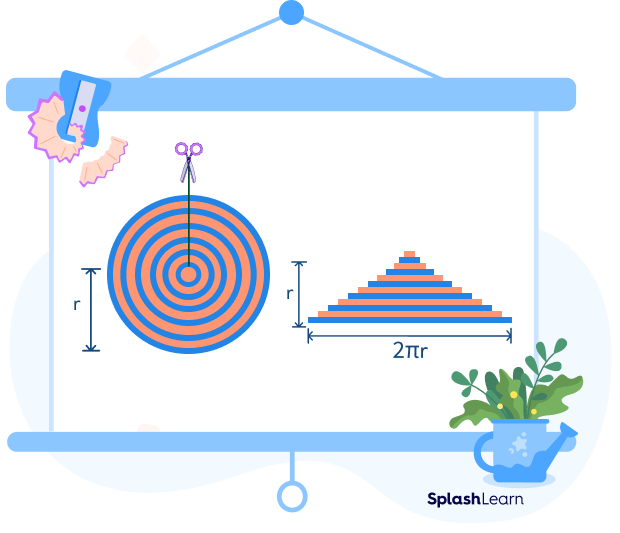
So, the area of the triangle (A) will be equal to the area of the circle. We have
Since, Area of a triangle $= \frac{1}{2}$ × base × height
So, putting the values from the figure into the formula
A $= \frac{1}{2} × (2\pi r) × r$
A = πr2
Real-world Examples of Applications of Area of a Circle
Let us take a couple of real-world applications of the area of a circle.
Example: Tracy has a table with a circular tabletop having a diameter of 3 feet. Would a tablecloth with an area 5 square feet be sufficient for covering the tabletop?

The radius of the tabletop will be half of the diameter.
$r = \frac{d}{2} = \frac{3}{2} = 1.5$ feet
Now, the area of the circular tabletop can be calculated using the formula:
A = πr2
A = π(1.5)2
A = 7.065 square feet
Thus, the tablecloth having an area 5 square feet won’t be enough to cover the tabletop.
Such a calculation is useful in day-to-day life scenarios to know the precise measurements of circular objects, thus minimizing the wastage of money and resources.
Facts about Area of a Circle
- The word “circle” itself comes from the Latin word “circulus,” meaning “a small ring.”
- Archimedes is known for his method of exhaustion, which involved inscribing and circumscribing polygons around a circle to approximate its area.
Conclusion
In this article, we learned how to calculate the area of a circle. We discussed formulas used to find the area of a circle based on the information known to us. We also derived the formula for the area of a circle using the area of a rectangle and area of a triangle. Now, let’s solve a few examples and practice MCQs.
Solved Examples on Area of a Circle
Example 1: If the diameter of a circular garden is 50 feet, find the area of the garden.
Solution:
Diameter of the circular garden (d) = 50 feet
The radius of the circular garden (r) $= \frac{d}{2} = 25$ feet
The area of the circular garden (A) = πr2
A = π(25)2
A = 625π square feet
Therefore, the area of the circular garden is 625π square feet.
Example 2: Calculate the area of a circle with a radius of 10 feet in terms of π.
Solution:
Radius (r) = 10 feet
The area of the circle (A) = πr2
A = π(10)2
A = 100π
Therefore, the area of the circular swimming pool is 100π square feet.
Example 3: What is the area of a circular window with a diameter of 3 feet?
Solution:
Diameter (d) = 3 feet
Radius (r) $= \frac{d}{2}$
r = 1.5 feet
So, A = πr2
A $= \pi \times (1.5)^{2}$
A = 2.25π
Therefore, the area of the circular window is 2.25π square feet.
Example 4: What is its area if a circular table measures 12π feet around its edge?
Solution:
Circumference of the circular table (C) = 12π
The area of the circular table when the circumference is given $= A = (\frac{C}{2π})^{2}$
A $= (\frac{12\pi}{2\pi})^{2}$
A = 62
A = 36 feet2
So, the area of the circular table is 36 feet2. We have another way to find out the area of the circular table when its circumference is provided.
A $= \frac{C^{2}}{4\pi}$
A $= \frac{12\pi^{2}}{4\pi}$
A $= \frac{144\pi}{4\pi}$
A = 36 square feet
Example 5: If a pizza restaurant charges $0.10 per square inch of pizza, what would be the cost of a pizza with a 14-inch diameter? (Round to the nearest whole number.)
Solution:
Diameter of the pizza = 14 inches
Radius of the pizza $= \frac{14}{2} = 7$ inches
We need to calculate the area first. For the area of the pizza, we can use the formula (A) = πr2
A = π × 72 = 49π square inches
Cost per square inch = $0.10
Cost of a pizza with 49π square inches area $= 49\pi \times \$0.10 = \$15.386 = \$15$ (Rounded to the nearest whole number.)
Therefore, the cost of the pizza is $\$15$.
Practice Problems on Area of a Circle
Area of a Circle - Definition, Formula, Derivation, Examples, FAQs
What is the area of a circle whose diameter is 8 units?
d = 2 units
r = 4 units.
A $= \pi r^{2} = \pi (4)^{2} = 16\pi$ square units
What is the radius of a circle with an area of 36π square inches?
A $= \pi r^{2}$
$36\pi = \pi r^{2}$
$r = \sqrt{36} = 6$ inches.
What is the area of a circle with a circumference of 18π units?
$C = 2\pi r$
Thus, $r = \frac{C}{2\pi} = \frac{18\pi}{2\pi} = 9$ units
Now, we can put the value of r into the area formula to calculate the area of the circle.
A $= \pi r^{2}$
A $= \pi(9)^{2} = 81\pi\; unit^{2}$
What is the area of a unit circle?
Radius of unit circle = 1 unit
A $= \pi r^{2} = \pi (1)(1) = \pi$ square units
Frequently Asked Questions about Area of a Circle
What is the formula for the area of a circle?
Area of a circle $= \pi r^{2}$, where r is the radius of the circle.
Can the area of a circle be negative?
The area of a circle can never have a negative value. The area of a circle is the amount of space it encloses given by A = πr2 . Both π and r are positive, thus area is always a positive value.
Is the radius of a circle a negative or a positive value?
The radius of a circle is always a positive value and not a negative one. The radius of a circle is the distance from the center to any point on its boundary. It is always a positive value as per its definition.
Is the area and circumference of a circle directly proportional to the radius?
The area of a circle is directly proportional to the square of radius. The circumference of a circle is directly proportional to the radius.
What is meant by the surface area of a circle?
The surface area is a term used in reference with three-dimensional objects. It refers to the total area of all its faces or surfaces. A circle is a plane two-dimensional shape, so it does not have a “surface area”; instead, it just has an area. So, the surface area of a circle is nothing but its area.