Difference between Fraction and Rational Number –  Definition, Examples

What Is the Difference between a Fraction and a Rational Number?

The difference between rational numbers and fractions lies in the fact that the numerator and denominator of a fraction are whole numbers $(\text{denominator} \neq 0)$, whereas the numerator and denominator of rational numbers are integers $(\text{denominator} \neq 0)$.

Rational numbers and fractions are two of the most commonly used terms in mathematics. They frequently cause confusion because of how similar they appear. Although these fundamental mathematical concepts have some connection, they are not the same. So, ​​what is the difference between a rational number and a fraction? Let’s explore in this article.

Before we learn the difference between the two terms, let’s understand what fractions and rational numbers are!

What Is a Fraction?

A fraction represents a part of a whole. A fraction is any number of the type $\frac{a}{b}$, where a and b are both whole numbers, and $b \neq 0$. 

A fraction has two parts. The number on the top is called the numerator. It tells how many equal parts of the whole or collection are taken. The number on the bottom is called the denominator.  It shows the total number of equal parts the whole is divided into or the total number of the same objects in a collection. 

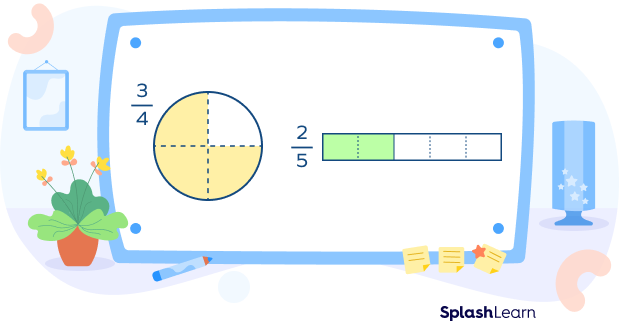
If you divide a circle in quarters (4 equal parts), three parts represent the fraction $\frac{3}{4}$.

If you divide a circle in 5 equal parts, two parts represent the fraction $\frac{2}{5}$.

There are different types of fractions based on the values of numerator and denominator.

Types of Fractions
1. Proper fractions: Their numerator is less than the denominator. They lie between 0 and 1. For example, $\frac{1}{5}$ and $\frac{2}{7}$
2. Improper fractions: Their numerator is greater than the denominator. They are always greater than or equal to 1. For example, $\frac{11}{7}$ and $\frac{6}{5}$.
3. Mixed Fractions: These are fractions that are made up of a whole number and a proper fraction. They are always greater than 1. For example, $4\frac{3}{4}$ and $2\frac{1}{3}$.
4. Equivalent fractions: These are fractions whose numerators and denominators are different, but still they represent the same value. For example, $\frac{2}{4}$ and $\frac{3}{6}$ are equivalent fractions, because they are equivalent to the fraction $\frac{1}{2}$.
5. Like Fractions: Two fractions whose denominator is the same. Example: $\frac{2}{4}$ and $\frac{1}{4}$
6. Unlike Fractions: Two fractions whose denominator is not the same. Example: $\frac{2}{3}$ and $\frac{1}{4}$

What Are Rational Numbers?

Rational numbers are numbers that can be written in the form $\frac{p}{q}$, where p and q are integers and $q \neq 0$. 

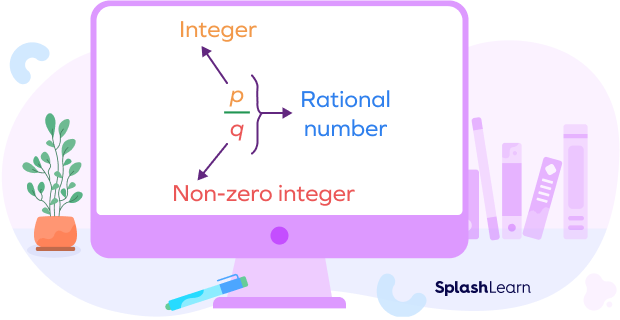
A rational number is any number that can be expressed as a fraction $\frac{p}{q}$, where both the numerator and denominator are integers, and the denominator is not 0. If a number cannot be expressed in this way, then it’s an irrational number.

Any integer can be written as a rational number. Thus, all integers are rational numbers.

For example, 5 can be expressed as $\frac{5}{1}$ . Both the numerator (5) and denominator (1) are integers, and the denominator is not 0. Thus, 5 is a rational number.

All fractions are rational numbers.

For example, $\frac{1}{2},\; \frac{4}{3}$, and $\frac{20}{450}$ are all rational numbers.

All terminating decimals are rational numbers.

For example, take the decimal number 0.5. This can be converted to $\frac{1}{2}$, which means it’s a rational number.

All non-terminating but repeating decimals are rational numbers.

For example, 0.323232…, 0.6666…, etc., are rational numbers.

Difference between a Rational Number and a Fraction Chart

Fraction vs. Rational Numbers
Fraction	Rational numbers
A fraction represents parts of a whole. Its numerator represents the number of parts taken. The denominator represents the total number of parts the whole is divided into.	Rational numbers include integers, natural numbers, whole numbers, fractions, numbers that can be written as fractions, decimals (terminating decimals and repeating decimals).
Written in the form of $\frac{a}{b}$, where a and b are whole numbers, and $b \neq 0$.	Rational numbers are numbers that can be written in the form $\frac{p}{q}$, where p and q are integers and $q \neq 0$.
All fractions are rational numbers.	All rational numbers are not fractions.
Fractions cannot be negative.	Rational numbers can be negative.
For example: $\frac{5}{2} ,\; \frac{7}{9},\; 5\frac{1}{3}$	For example: $\frac{11}{3},\; \frac{-4}{7}$

Similarities between Fractions and Rational Numbers

• They appear the same due to the similarities in their representations. Both fractions and rational numbers are expressed as a ratio of numbers.

• All fractions and rational numbers are real numbers.

• The denominator of both fractions and rational numbers is 0.

Facts about Difference between Fractions and Rational Numbers

Conclusion

In this article, we learned about fractions, rational numbers, and the difference between them.

Are fractions rational numbers? The answer is yes, but all rational numbers are not fractions. 

Let’s solve some examples and practice problems.

Solved Examples on the Difference between Fractions and Rational Numbers

1.  Identify rational numbers and fractions: $\frac{5}{4},\; \frac{-2}{3},\; \frac{7}{-8},\; \frac{6}{8},\; \frac{5}{10}$.

Solution: 

Rational numbers can have both positive and negative integer ratios when stated as fractions.

Thus, $\frac{5}{4},\;  \frac{6}{8},\; \frac{5}{10},\; \frac{-2}{3},\; \frac{7}{-8}$  all are rational numbers. 

54 ,  68 , 510 are fractions. All fractions are rational numbers. Thus, $\frac{5}{4},\; \frac{6}{8},\; \frac{5}{10}$  all are fractions as well as rational numbers. $\frac{-2}{3},\; \frac{7}{-8}$ are not fractions.

2. Determine whether the following rational numbers are fractions or not:

(i) $\frac{1}{3}$      (ii) $\frac{6}{3}$        (iii) $\frac{-5}{-3}$

Solution: 

(i) $\frac{1}{3}$ 

$\frac{1}{3}$ is a fraction since both the numerator (1) and the denominator (3) are whole numbers. This is a unit fraction or a proper fraction.

(ii) $\frac{6}{3}$

$\frac{6}{3}$ is a fraction since both the numerator (6) and the denominator (3) are whole numbers. This is an improper fraction.

(iii) $\frac{-5}{3}$

$\frac{-5}{3}$ is not a fraction since the numerator (-5) is not a whole number. 

3. At a drama camp, there are 16 art tutors and 13 drama tutors. What fraction of the total number of tutors teach drama? 

Solution: 

The numerator of the fraction $(p) =$ Number of drama tutors

The denominator of the fraction $(q) =$ The total number of tutors in the camp. 

The fraction of drama tutors $=$ Number of drama tutors/ The total number of tutors

$\frac{p}{q} = \frac{13}{16 +13}$

$\frac{p}{q} = \frac{13}{29}$

4. Identify whether 7 is a rational number or a fraction or both. 

Solution: 

 7 can be expressed as $\frac{7}{1}$ which is a positive number ratio. So, it is a fraction. It is an improper fraction. It is a rational number as well since it can be written in the form of $\frac{p}{q},\; q \neq 0$, where both p and q are integers.

5. Is $\frac{2}{-5}$ a fraction? Is it a rational number?

Solution: 

The number $\frac{2}{-5}$ is a rational number since it is in the form of $\frac{p}{q},\; q \neq 0$, and both p and q are integers.

However, it is not a fraction since a fraction is always positive. Note that $\frac{2}{5}$ is a fraction (a proper fraction).

Practice Problems on Fractions and Rational Numbers

Frequently Asked Questions on Fractions and Rational Numbers