Dilation in Geometry – Definition, Scale Factor, Properties, FAQs

What Is Dilation in Geometry?

Dilation is one of the five important transformations in geometry. Dilation, in math, involves transforming a figure by either shrinking or enlarging it while maintaining its shape. 

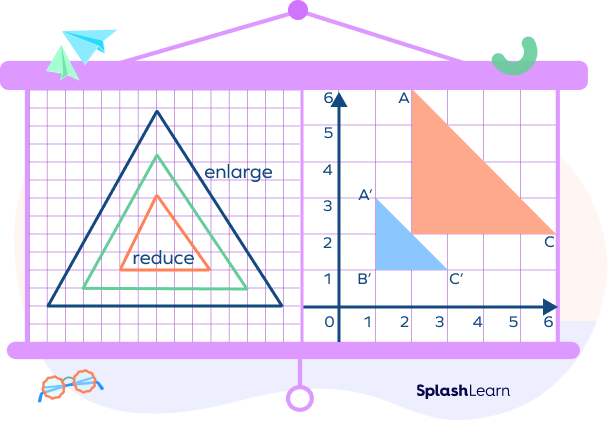
Note that dilation changes the position and size of an object but not its shape.

Dilation in Geometry: Definition

Dilation is a geometric transformation that alters the size of a figure, either by reducing or enlarging it, still maintaining its shape. 

Center of Dilation

The center of dilation is a fixed reference point around which the dilation occurs. 

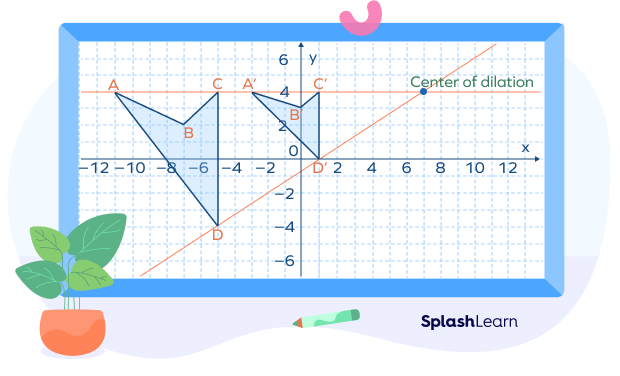
Each point on the object that is dilated moves toward or further away from the center and preserves the same proportionate relationship to the center. It may be located inside, outside, or on a figure.

Scale Factor in Dilation

In the dilation transformation, the coordinates of each point by a constant factor called the scale factor or dilation factor. Dilation preserves the shape of the figure, but its size changes relative to the center of dilation.

The scale factor is commonly denoted by r or k, which determines the amount of enlargement or reduction. The scale factor cannot be zero.

• The image is enlarged if the scale factor is GREATER THAN 1. 

(r > 1 means the figure is enlarged.)

• The image is contracted if the scale factor is LESS THAN 1. 

(0 < r < 1 means the figure is shrinked.)

• The image remains the same if the scale factor is EQUAL TO 1. 

(r = 1 means that the figure stays the same.)

The scale factor determines the degree of enlargement or reduction in a dilation. It represents the ratio of corresponding lengths between the original figure and its dilated image. We compare the corresponding lengths of any two sides or segments to find the scale factor.

Formula for the Scale Factor in Dilation

The formula for calculating the scale factor in dilation is:

Scale Factor $= \frac{Length\; of\; Corresponding\; Side\; in\; Dilated \;Figure}{Length\; of\; Corresponding \;Side \;in \;Original\; Figure}$

Scale factor = Dimension of the new shape ÷ Dimension of the original shape

How to Find the Scale Factor of Dilation

We can easily find the scale factor if we know the lengths of both the original and dilated images are known.

1. Note down the lengths of corresponding sides of the original figure and the dilated image.
2. Find the ratio of corresponding sides.
3. The result is the scale factor.

How to Find the Center of Dilation

If the coordinates $(x_{1}, y_{1})$ are dilated to $(x_{2}, y_{2})$ and the scale factor is r, then the center of dilation $(h, k)$ is given by

$h = \frac{rx_{1} – x_{2}}{r – 1}$

$k = \frac{ry_{1} – y_{2}}{r – 1}$

Formulas for Dilation in the Coordinate Geometry

The dilation formula expresses the relationship between the coordinates of the vertices of the original figure and its dilated image. 

• Given a point $(x, y)$ and a center of dilation $(h, k)$ with a scale factor of r, the coordinates of the dilated point $(x’, y’)$ can be found using the following formulas:

$x’ = h + r(x – h)$

$y’ = k + r(y – k)$

Thus, given a scale factor r and a center of dilation is $(h, k)$, the dilation formula for a point $(x, y)$ is

$(x, y) \rightarrow (h + r (x – h),k +r (y – k))$

• When the scale factor is r, where $0 \lt r \lt \infty$, and the center of dilation is $(0, 0)$, then the coordinates $(x, y)$ of the original figure are changed to $(rx, ry)$.

$(x, y) \rightarrow (rx ,ry)$

Horizontal Dilation

The dilation transformation of a function $y = f(x)$ dilated horizontally by a scale factor k is given by

$y = f(kx)$

This kind of transformation is called a horizontal dilation. It makes the figure taller or shorter. Height changes but the shape stays the same. The horizontal dimensions remain the same.

Vertical Dilation

The dilation transformation of a function $y = f(x)$ dilated vertically by a scale factor k is given by 

$y = k \times f(x)$

This kind of transformation is called a Vertical dilation. It makes the figure wider or narrower. Width changes but the shape stays the same. The vertical dimensions are not affected.

Properties of Dilation

• The distance between the points is the only thing that changes during the dilation process. It implies that the sides of the original and dilated images may differ in length.
• Corresponding angles of both the figures stay the same.
• Parallel lines in the original figure stay parallel in the dilated figure.
• Perpendicular lines in the original figure stay perpendicular in the dilated figure.
• The perimeter of a dilated figure is directly proportional to the scale factor.

Dilation of Shapes: Examples

Dilation of a line segment Center: OriginScale factor: 3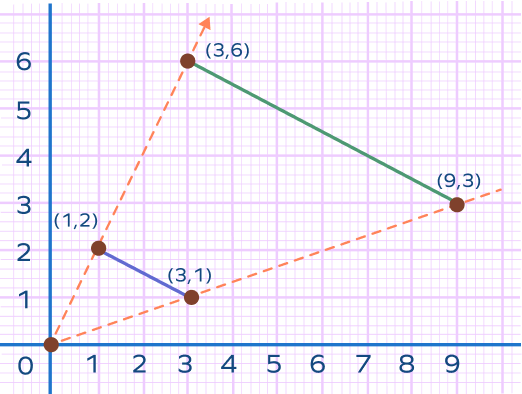
Dilation of a triangle Center: OriginScale factor: 3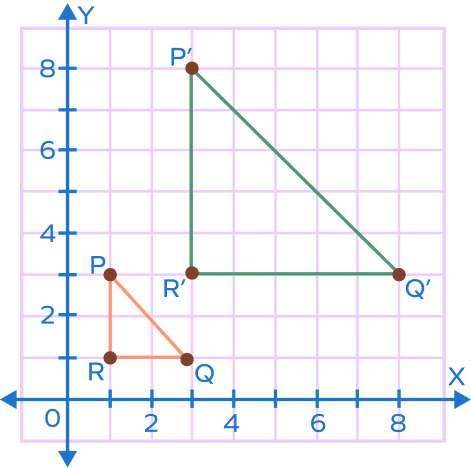
Dilation of a rectangle Center: OriginScale factor: 2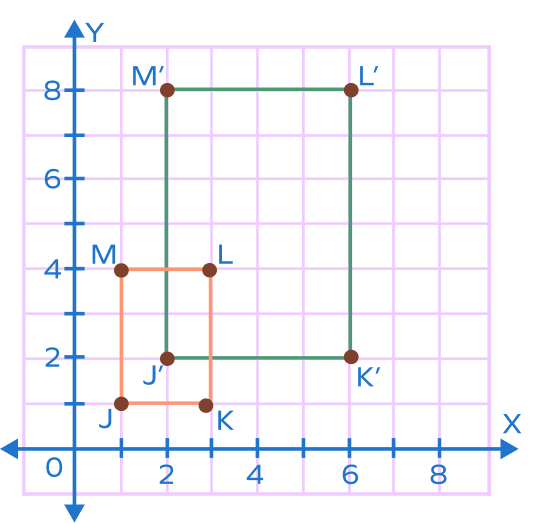
Dilation of a square Center: OriginScale factor: 2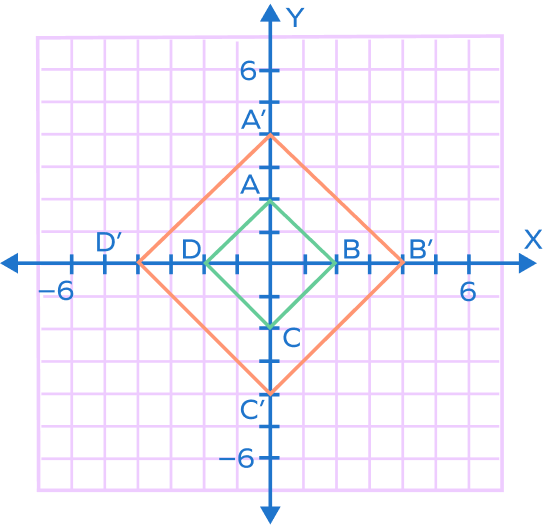

Facts about Dilation in Geometry

Conclusion

In this article, we learned about the dilation transformation in geometry and important terms associated with the concept such as center of dilation, scale factor, formulas, etc. Let’s use these concepts to solve a few solved examples and practice problems.

Solved Examples on Dilation in Geometry

Example 1: A triangle ABC with AB = 6, BC = 8, and CA = 10, is dilated by a scale factor of 2 with the center of dilation at the origin. Find the lengths of the corresponding sides in the dilated triangle.

Solution: To find the lengths of the corresponding sides, we multiply each side of the original triangle by the scale factor.

AB = 6, BC = 8, and CA = 10

We know that

Scale Factor $= \frac{Length\; of\; Corresponding\; Side\; in\; Dilated\; Figure}{Length\; of\; Corresponding\; Side\; in\; Original\; Figure}$

$2 = \frac{A’B’}{AB} = \frac{B’C’}{BC} = \frac{A’C’}{AC}$

Using the dilation formula:

$A’B’ = 2 \times AB = 2 \times 6 = 12$ units

$B’C’ = 2 \times BC = 2 \times 8 = 16$ units

$A’C’’ = 2 \times AC = 2 \times 10 = 20$ units

Example 2: ▵PQR is dilated by the scale factor of 0.5 with the center of dilation at origin. If P ≡ (1, 2), Q ≡ (3, 5), R ≡ (2, 8), find the coordinates of the vertices of the dilated triangle ▵P’Q’R’.

Solution: To find the dimensions of the corresponding rectangle, we multiply each dimension of the original rectangle by the scale factor.

If the scale factor is 0.5, then every coordinate point of the original triangle is multiplied by the scale factor 0.5.

$(x, y)\rightarrow (0.5 x, 0.5 y)$

$P ≡ (1, 2) \rightarrow P’ ≡ (0.5, 1)$

$Q ≡ (3, 5) \rightarrow Q’ ≡ (1.5, 2.5)$

$R ≡ (2, 8) \rightarrow Q’ ≡ (1, 4)$

Example 3: Given a circle with a radius of 5 units and a center at point O. Dilate the circle by a scale factor of $\frac{1}{2}$ with the center of dilation at point origin. Find the radius of the corresponding circle in the dilated image.

Solution: To find the radius of the corresponding circle, we multiply the radius of the original circle by the scale factor.

Note that the scale factor is 0.5 (lies between 0 and 1), thus the dilated circle will be exactly half of the original circle.

Using the dilation formula:

$r’ =$ scale factor$\times r$

$r’ = (\frac{1}{2}) \times$ radius

$r’ = (\frac{1}{2}) \times 5$

$r’ = 2.5$ units

Example 4: Perimeter of a triangle is 20 units. It is dilated by the scale factor of 3 with the center of dilation at the origin. What will be the perimeter of the dilated triangle?

Solution: 

When a figure is dilated, we know that the corresponding sides are proportional.

Thus, the length of each side l’ of the dilated figure can be given as

l’ = scale factor$ \times l$

where l is the length of the corresponding original side.

Perimeter of original triangle = Sum of all sides 

Perimeter of dilated triangle = Scale factor $\times$ (Perimeter of original triangle) 

Perimeter of dilated triangle $= 3 \times 20$

Perimeter of dilated triangle = 60 units

Example 5: Find the center of dilation and scale factor.

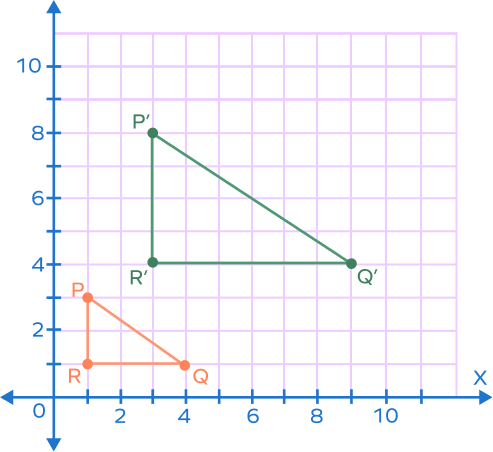
Solution: 

Step 1: Let’s note down the coordinates of the vertices of the original triangle (pre-image) and the dilated triangle (image). 

$P = (1, 3) , P’ = (3, 8)$

$Q = (4, 1) , Q’ = (9, 4)$

$R = (1, 1), R’ = (3, 4)$

Step 2:

$PR = 2 units, P’R’ = 4 units$

$QR = 3 units, Q’R’ = 6 units$

$PQ = \sqrt{13}$ units, P’Q’ $= 2\sqrt{13}$ units

Step 3:

Based on the length of sides, we can see that the lengths of corresponding sides in the dilated triangle are two times the length of the original triangle.

Thus, scale factor $= r = 2$

Step 4:

Let the center of dilation be $(h, k)$.

If the coordinates $(x_{1}, y_{1})$ are dilated to $(x_{2}, y_{2})$ and the scale factor is r, then the center of dilation (h, k) is given by

$h = \frac{rx_{1} – x_{2}}{r – 1}$

$k = \frac{ry_{1} – y_{2}}{r – 1}$

Here, $P = (1, 3)$ changes to $P’ = (3, 8)$.

$(x_{1}, y_{1}) = (1, 3)$

$(x_{2}, y_{2}) = (3, 8)$

$h = \frac{rx_{1} – x_{2}}{r – 1} = \frac{2 – 3}{2 – 1} = -1$

$k = \frac{ry_{1} – y_{2}}{r – 1} = \frac{6  –  8}{2 – 1} = -2$

Thus, the center of dilation is $(-1, -2)$.

Another way:

We know that, the coordinates $(x, y)$ change to $(h + r (x – h),k + r (y – k))$.

Here, the changed coordinates must be of the form $(h + 2 (x – h), k +2 (y – k))$.

Since $P = (1, 3)$ changes to $P’ = (3, 8)$, we have

Original coordinates: $(x, y) = (1, 3)$

Dilated coordinates: $(h + 2 (x – h), k + 2 (y – k)) = (3, 8)$

$h + 2 (1 – h) = 3$ and $k + 2 (3 – k) + k = 8$

$h + 2 (1 – h) = 3$ and $k +2 (3 – k) + k = 8$

$h + 2 – 2h = 3$ and $k + 6 – 2k = 8$

$-h + 2 = 3$ and $-k + 6 = 8$

$h = -1$ and $k = -2$

Thus, the center of dilation is $(-1, -2)$.

Practice Problems on Dilation in Geometry

Frequently Asked Questions about Dilation in Geometry