What Is the Equation of a Line?
The equation of a line is the algebraic equation that defines the relationship between coordinates (x, y) of any point on the line. It gives us important information such as slope, intercepts, etc.
Through the equation of a line, we can easily figure out if the point lies on the line or not. All the points located on the line must satisfy the equation. The equation of a line is a linear equation in both x and y.
There are different forms of writing the equation of a line, depending on the information provided.
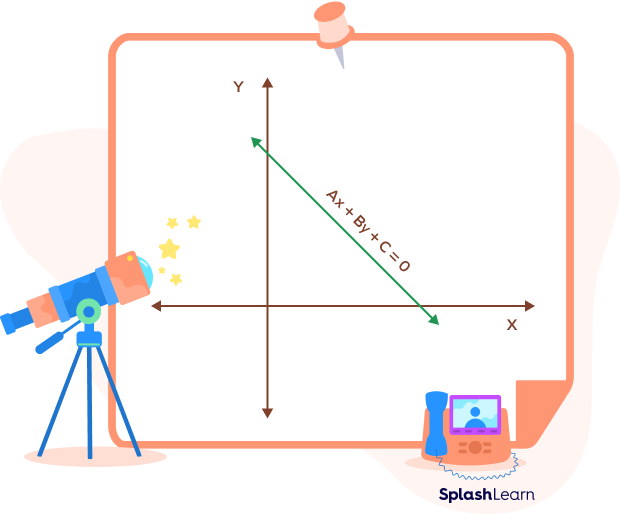
The general form to define the equation of a line is $ax + by + c = 0$, where
- x and y are variables that represent the coordinates of any point on the line,
- a,b,c are constants (integers) such that “a” and “b” cannot be simultaneously 0, and “a” is non-negative.
The standard form is given as $ax + by = c$, where
- x and y are variables that represent the coordinates of any point on the line,
- a,b,c are constants (integers) such that “a” and “b” cannot be simultaneously 0, and “a” is non-negative.
Recommended Games
Equation of a Line Formulas
Depending on the known parameters for the line, five distinct formulas can be used to determine the equation of a line.
- Point Slope Form of Equation of a Line
The slope point form of equation of a line that has slope m and passes through a point $(x_{1}, y_{1})$ is expressed as:
$(y – y_{1}) = m(x – x_{1})$
- Two-Point Form of Equation of a Line
The two-point form of the equation of a line that passes through the points $(x_{1},\; y_{1})$ and $(x_{2},\; y_{2})$ is expressed as:
$(y – y_{1}) = \frac{(y_{2} – y_{1})}{(x_{2} – x_{1})}(x – x_{1})$
- Slope-Intercept Form
The slope-intercept form of the equation of a straight line is expressed as:
$y = mx + b$
where
m is the slope of the line,
b is the y-intercept (the point where the line intersects the y-axis.)
- Intercept Form
The intercept form of equation of a straight line is expressed as:
$\frac{x}{a} + \frac{y}{b} = 1$
where
a is the x-intercept of the line, and
b is the y-intercept of the line.
Recommended Worksheets
How to Find the Equation of a Line
Depending on the information provided, you can choose the form to determine the equation of a line.
Step 1: Notice the data provided in the given problem.
Step 2: Choose the appropriate form of the equation.
- If the coordinates of one point on the line $(x_{1}, y_{1})$ and the slope m are given, use the point-slope form.
- If the coordinates of two points lying on the line are given, use the two-point form equation of a line formula
- If the slope m and the y-intercept b are given, use the slope-intercept form of the equation of a straight line.
- If both the x-intercept and y-intercept are given, use the intercept form of the equation of a line.
Facts about Equation of a Line
- The equation of a straight line with slope m, passing through the origin is given by
- y = mx.
- You can find parallel and perpendicular lines using equations of two lines.
- Two lines are parallel if and only if they have the same slope.
- Two lines are perpendicular if the product of their slopes is -1.
- The equation of a vertical line is of the form x = a, where ‘a’ represents a constant. Vertical lines have an undefined slope.
- The equation of a horizontal line is of the form y = b, where ‘b’ represents a constant. Horizontal lines have a slope of zero.
Conclusion
In this article, we learned about the equation of a line, its different forms based on the kind of information available to us, and related examples. Let’s solve a few examples and practice MCQs for better comprehension.
Solved Examples on Equation of Line
1. Determine the equation of the line passing through the points (1, 3) and (2, 5).
Solution:
$(x_{1},\;y_{1}) = (1,\;3)$
$(x_{2},\;y_{2}) = (2,\;5)$
We use the two-point form of the equation of a line given by
$(y – y_{1}) = \frac{(y_{2} – y_{1})}{(x2 – x1)} (x – x_{1})$
$(y – 3) = \frac{(5 – 3)}{(2 – 1)}(x – 1)$
$(y – 3) = (\frac{2}{1})(x – 1)$
$y – 3 = 2 (x – 1)$
$y – 3 = 2x – 2$
$y = 2x – 5$
Thus, the slope-intercept form equation will be $y = 2x – 5$.
2. Find the equation of a line with slope 3 and y-intercept 2.
Solution:
Slope $= m = 3$
y-intercept $= b = 2$
Slope-intercept form is given by $y = mx + b$.
$y = (3)x + 2$
$y = 3x + 2$
3. Are the lines $x + y + 1 = 0$ and $x – y – 1 = 0$ perpendicular?
Solution:
Line 1: $x + y + 1 = 0$
We can write it as $y = – x – 1$
Slope $= -1$
Line 2: $x – y – 1 = 0$
We can write it as $y = x – 1$
Slope $= 1$
Product of two slopes $= (1) \times (- 1) = -1$
Thus, the two lines are perpendicular.
Practice Problems on Equation of Line
How to Find the Equation of a Line? Formula, Examples, FAQs
What is the point-slope form of the equation of a line?
The point-slope form of the equation of a line is $(y - y_{1}) = m(x - x_{1})$.
The equation of a line with slope -1 and passing through origin is
The equation of a line with slope -1 and passing through origin is $y = -x$.
We can rewrite is as $x + y = 0$.
Find the equation of the line parallel to $y = 3x - 1$.
Two lines are parallel if they have the same slope.
$y = 3x -1$ and $y = 3x + 1$ have the same slope $m = 3$.
Equation of a line having x-intercept 1 and y-intercept -2 is
Intercept form: $\frac{x}{a} + \frac{y}{b} = 1$
Here, $a = 1,\; b = -2$
$\frac{x}{1} + \frac{y}{(- 2)} = 1$
$-2x + y = -2$
$2x - y = 2$
Frequently Asked Questions about Equation of a Line
What are the equations of the x-axis and the y-axis?
The equation of the x-axis is y = 0.
The equation of the y-axis is x = 0.
How do you find the slope of a line using two points on it?
The slope of a line that passes through the points (x1, y1) and (x2, y2) is $\frac{(y_{2} – y_{1})}{(x_{2} – x_{1})}$.
Why do people usually prefer to use the slope-intercept form for the equation of a line?
The slope-intercept form is given by y = mx + b, where m is the slope and b is the y-intercept. It is special because you can easily identify the slope (m) and the y-intercept (b) of the line simply by looking at the equation.
How do you define the equation of a line?
The equation of a straight line is a linear algebraic equation that defines the relationship between coordinates of every point on the line and provides information such as about the slope, intercepts of the line.
How do you find the equation of a line if you know the coordinates of two points on the line?
If you know the coordinates of two points on the line, use the Two-Points form of the equation of a line.