What Is an Isosceles Obtuse Triangle in Math?
An isosceles obtuse triangle is a triangle in which one interior angle is an obtuse angle and the remaining two angles are equal and acute.
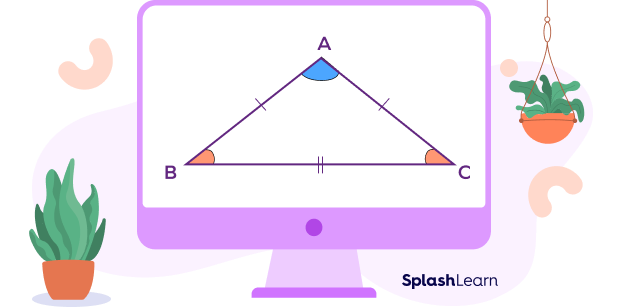
An isosceles triangle is a triangle which has two equal sides and the angles opposite to the equal sides are also equal. It has properties of both obtuse and isosceles triangles.
The question here is – Can an isosceles triangle be obtuse? Yes! An isosceles triangle can be obtuse!
If the third interior angle (non-equal angle) in an isosceles triangle is obtuse (lying between 90° and 180°), it is called an isosceles obtuse triangle. Note that the obtuse angle is made by the two equal sides.
Recommended Games
Isosceles Obtuse Triangle Definition
A triangle that has two equal sides (thus, isosceles); and one interior angle lying between 90° and 180° (hence, obtuse) is called an isosceles obtuse triangle.
The obtuse angle lies opposite to the longer side, and the other two angles are acute on equal sides.
Recommended Worksheets
Isosceles Obtuse Triangle Properties
- One interior angle is obtuse. Remaining two angles are acute and equal in measurement.
- Two sides are of equal length.
- Angles opposite to the equal sides are equal.
- The obtuse angle lies opposite to the longest side.
Isosceles Obtuse Triangle Formulas
There are several formulas of an isosceles obtuse triangle, such as, area, perimeter, semi-perimeter, height, etc. Let’s discuss different formulas associated with the isosceles obtuse triangle.
Height of an Obtuse Isosceles Triangle
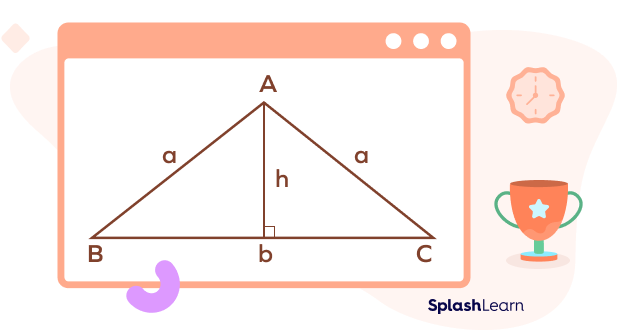
Consider the isosceles obtuse triangle △ABC.
To calculate the height of the triangle, we use the following formula:
| Height of isosceles obtuse triangle $= \frac{1}{2} \sqrt{4a^{2}\;-\;b^{2}}$ |
Here,
h is the height of the triangle
a is the length of two equal sides
b is the base of the triangle (the length of the unequal side)
Perimeter of Obtuse Isosceles Triangle
The perimeter of a triangle is the sum of the measure of all three sides of the triangle. The formula for perimeter of the isosceles obtuse triangle is as follows:
P = a + a + b
P = 2a + b
| Perimeter of isosceles obtuse triangle = 2a + b |
Semiperimeter of Isosceles Obtuse Triangle
The semiperimeter refers to half of the perimeter. The semiperimeter of an obtuse isosceles triangle is given by the following formula:
S $= \frac{2a + b}{2}$
| Semiperimeter of isosceles obtuse triangle $= \frac{2a + b}{2}$ |
Area of Isosceles Obtuse Triangle
There are three methods to find the area of an obtuse isosceles triangle:
- Area of Isosceles Obtuse Triangle Using Base and Height
We can calculate the area of an obtuse isosceles triangle with base b and height h as
Area $= \frac{1}{2} \times b \times h$
- Area of Isosceles Obtuse Triangle Using Heron’s Formula
Heron’s formula is used to calculate the area when we only know the lengths of the three sides of a triangle.
A $= \sqrt{s(s − a)(s − b)(s − c)}$
Here,
s is the semiperimeter.
a, b, and c are triangle sides.
In the case of an isosceles obtuse triangle, two of the sides are equal (a = b). So, we write
A $= \sqrt{s(s − a)^{2}(s − c)}$
A $= (s − a) \sqrt{s(s − c)}$
- Area of Isosceles Obtuse Triangle Using Apex Angle
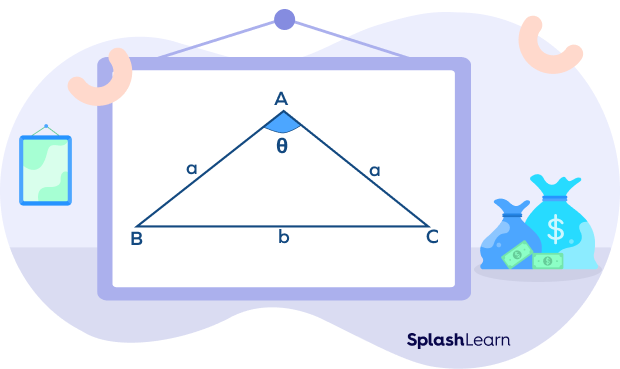
The apex angle (obtuse angle) is present between two equal sides of the obtuse isosceles triangle. The formula of the area using the apex angle is as follows:
A $= \frac{1}{2} a^{2} sin\theta$
Here,
is for the apex angle.
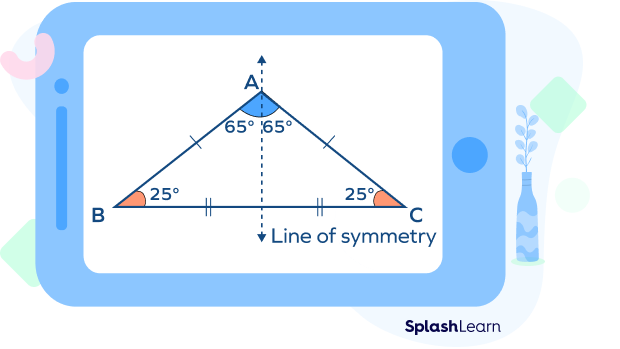
Isosceles Obtuse Triangle Lines of Symmetry
An isosceles obtuse triangle has only one line of symmetry. It coincides with the bisector of the apex angle (obtuse angle) formed between the two equal sides. It divides the triangle into two identical halves that are mirror images of each other. If you fold an obtuse isosceles triangle along the line of symmetry, two parts will superimpose on each other.
How to Construct an Obtuse Isosceles Triangle
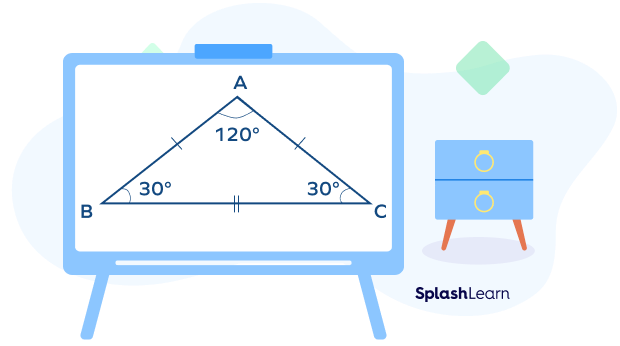
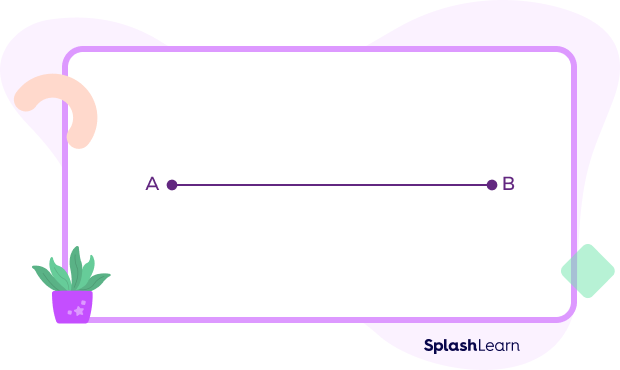
Let us consider constructing an isosceles obtuse triangle with two 30 degree angles and a 120 degree angle. Follow the steps given below to construct an obtuse isosceles triangle:
- Draw a baseline segment AB.
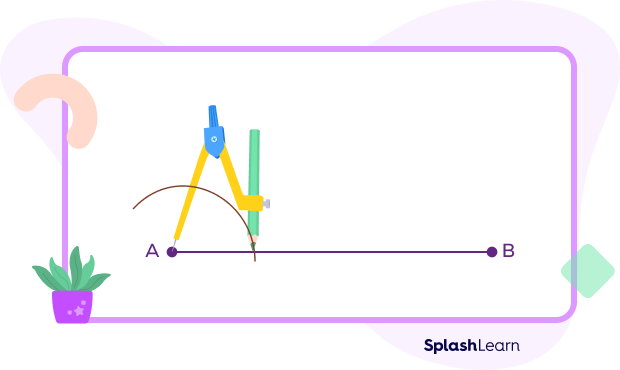
- Draw an arc by placing the compass at A keeping a suitable radius.
- Now place the compass at the point of intersection of the arc and the segment and draw another arc such that it cuts the first arc. (We did this to construct a 60 degree angle. All sides of an equilateral angle are equal and each angle measures 60 degrees. Thus, we kept the same radius when drawing bothe the arcs.)
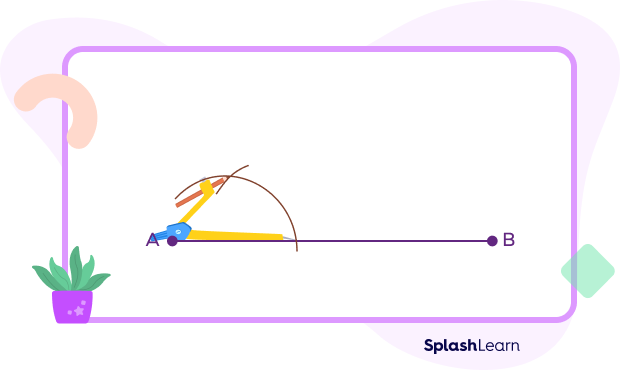
- Next, bisect the 60 degree angle to get a 30 degree angle. Use the two intersection points and draw two arcs that meet each other as shown below.
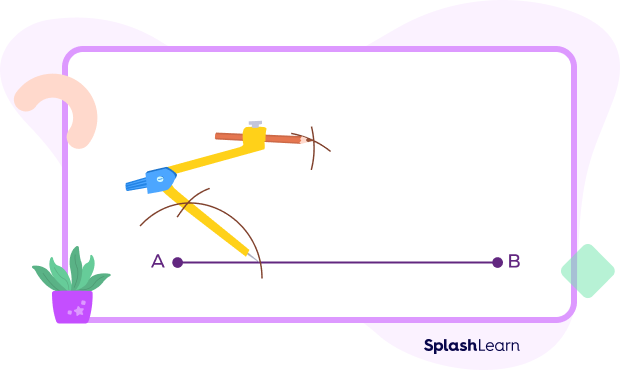
- Join the intersection point and the endpoint A.
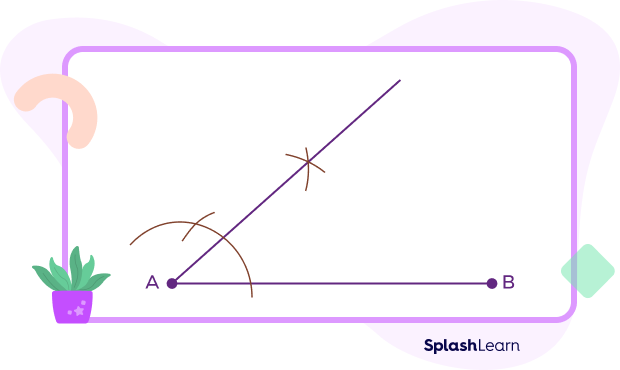
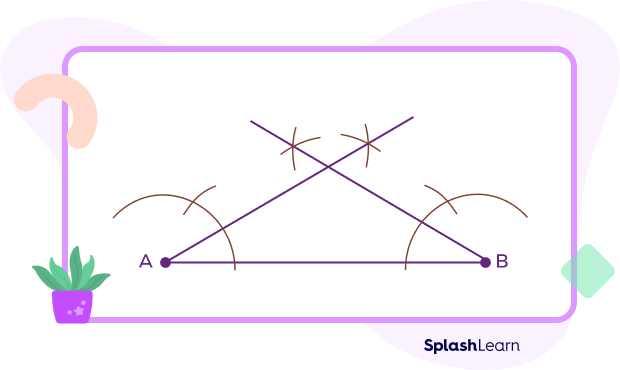
- Now, repeat the same steps using the endpoint B to consider a similar 30 degree angle.
Draw a line extending from endpoint B towards the point of interaction.
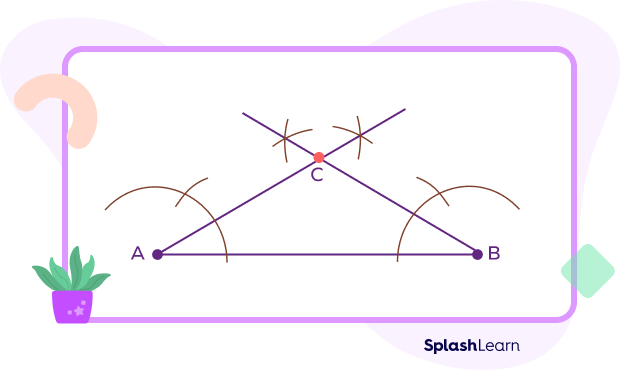
Join the points where the arcs intersect with the endpoints of the base to form an isosceles triangle. Name the new intersection point as C.
- Measure the angle C using a protractor, it will be 120 degrees, an obtuse angle.
Note: Do not change the angle of the compass, the distance between the pointer and pencil throughout your construction.
Facts about Isosceles Obtuse Triangle
- An isosceles obtuse triangle is a type of isosceles triangle whose one interior angle is an obtuse angle.
- The side which is opposite the obtuse angle is the longest side of the isosceles obtuse triangle.
- A triangle cannot be both an isosceles obtuse triangle and a right triangle because it contains an obtuse angle.
Conclusion
In this article, we learned about the definitions and important formulas related to obtuse isosceles triangles. Let us now navigate through the numerical section of the article, which covers solved examples and MCQ practice problems.
Solved Examples on Isosceles Obtuse Triangle
Example 1: If one of the base angles of an isosceles obtuse triangle measures 40°, find the remaining angles.
Solution:
Both base angles are equal in an isosceles triangle.
Thus, the other base angle will also be 40°.
The total of all angles in a triangle is 180 degrees. Let the measure of the obtuse angle be x degrees.
40° + 40° + x = 180°
80° + x = 180°
x = 180° – 100°
x = 100°
Therefore, the other base angle is 40°and the obtuse angle is 100°.
Example 2: An isosceles obtuse triangle has equal sides of 6 units and a base of 8 units. Calculate the height of the triangle.
Solution:
The length of equal sides (a) = 6 units
The length of the base (b) = 8 units
For calculating the height of the triangle, we will use the formula:
h $= \frac{1}{2} \sqrt{4a^{2} − b^{2}}$
On substituting the values of a and b into the formula:
h $= \frac{1}{2} \sqrt{4(6)^{2} − (8)^{2}}$
h $= \frac{1}{2}\sqrt{80}$
h $= \frac{1}{2} \times 8.94$ (approximately)
h = 4.47 units (approximately)
Example 3: The lengths of the sides of an isosceles obtuse triangle are as follows:
a = 7 units, b = 7 units, c = 10 units.
Use the Heron’s formula to calculate the area of an isosceles obtuse triangle.
Solution:
Heron’s formula to find the area of the triangle is given by
A $= \sqrt{s(s − a)(s − b)(s − c)}$
The semiperimeter “s” of the triangle is given by
$s = \frac{a + b + c}{2}$
$s = \frac{2a+b}{2}$ (two sides are equal.)
$s = \frac{(2(7) + 10)}{2}$
s = 12 units
The area is calculated as
A $= \sqrt{12(12 − 7)(12 − 7)(12 − 10)}$
A $= \sqrt{(12 \times 5 \times 5 \times 2)}$
A $= \sqrt{600}$
A ≈ 24.49 square units
Example 4: If an obtuse isosceles triangle has one side length of 6 units and a base length of 8 units, calculate the perimeter of the triangle.
Solution:
Equal sides (a) = 6 units
Base (b) = 8 units
The other side is also equal to ‘a’(isosceles property).
The formula for calculating the perimeter of an obtuse isosceles triangle is:
P = 2a + b
Putting the values in the formula, we get
P = 2(6) + 8
P = 12 + 8
P = 20 units
Practice Problems on Isosceles Obtuse Triangle
Isosceles Obtuse Triangle – Definition, Formulas, Examples, FAQs
How many equal sides does an isosceles obtuse triangle have?
There are two equal sides in an isosceles triangle.
How many obtuse angles are there in an isosceles obtuse triangle?
In an isosceles obtuse triangle, there is one obtuse angle.
In an isosceles obtuse triangle, one interior angle measures 20°. What is the measure of the obtuse angle?
There are two equal acute angles and one obtuse angle in an isosceles obtuse triangle.
Thus, 20° + 20° + obtuse angle = 180°
Obtuse angle = 140°
Identify the isosceles obtuse triangle using the measurement of three interior angles.
We need to look for a combination with two acute angles that are equal and one obtuse angle.
Thus, the combination of 35°, 35°, 110° represents an isosceles obtuse triangle.
Frequently Asked Questions about Isosceles Obtuse Triangle
How many obtuse angles are there in an obtuse isosceles triangle?
There is just one obtuse angle in an obtuse isosceles triangle.
Can an isosceles obtuse triangle be a right triangle?
No, an isosceles obtuse triangle can’t be a right triangle. An isosceles obtuse triangle has an obtuse angle which is more than 90 degrees.
How to find a missing angle in an obtuse isosceles triangle?
To determine the value of the missing angle, simply subtract the sum of the two given angles from 180 degrees. This will give you the measurement of the angle that is not known.
Is an isosceles obtuse triangle equilateral?
No, it is not possible for an isosceles obtuse triangle to be an equilateral triangle. An equilateral triangle has all three equal measuring angles, i.e., 60 degrees. It is not possible for an obtuse triangle to have 60 degrees angles.
What are the types of isosceles triangles?
1) Acute isosceles triangle, 2) Obtuse isosceles triangle, and 3) Right isosceles triangles.
What does an obtuse triangle look like?
In an obtuse triangle, there is one obtuse angle and two acute angles. The side opposite to the obtuse angle is the longest side of the triangle.




























