Not Equal Sign – Definition, Example, Facts, Practice Problems

What Is the “Not Equal Sign” in Math?

The “not equal sign” or “not equal to sign” is used to represent two quantities that are not equal. When two values are not equal, then the “not equal sign $(\neq)$” can be used to show the inequality. 

Other names of the $\neq$ sign:  Not equal / does not equal / not equal to / unequal

There are different signs of comparison in math, such as $\lt,\; \gt,\le ,\ge ,\neq$ , etc., that help us to avoid the effort of writing long mathematical statements or expressions, or to avoid the repetition of the terms like “greater than” and “lesser than.” 

For example, we simply use the “equal to sign $(=)$” in mathematical equations to show that L.H.S. value equals the R.H.S. value. Similarly, the “not equal to sign” simply states that the quantity or value on L.H.S. is not equal to the value on R.H.S.

Comparison Sign	Meaning
$=$	Equal to
$\neq$	Not equal
$\lt$	Less than
$\gt$	Greater than
$\le$	Less than or equal to
$\ge$	Greater than or equal to

What Do You Mean by “Not Equal”?

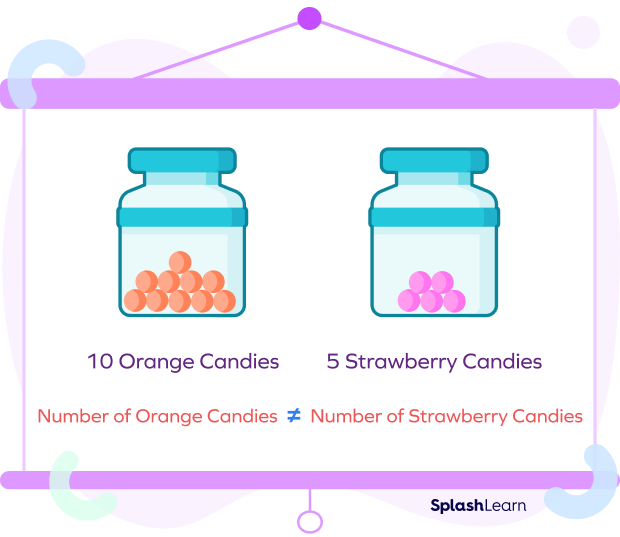
When we say $A \neq B$, it means that the quantity A is not equal to the quantity B in value.

Not Equal: Definition

Two quantities are said to be not equal to each other if they do not have the same value, rank, size, etc. 

Examples:

• Price of a tomato $\neq$ Price of an apple
• Phone number of Roy $\neq$ Phone number of Jack
• Size of a tennis ball $\neq$ Size of a basketball

Not Equal Symbol

It is represented by two horizontal parallel lines cut by a slanted line. It is “equal to sign” cut by a slanted line (a slashed equal sign).

Not equal symbol: $\neq$

What Is the Use of Not Equal Sign in Math?

We can use the not equal sign whenever we want to convey that the given two numbers/quantities are unequal. 

Example: Are the perimeters of the two given figures equal?

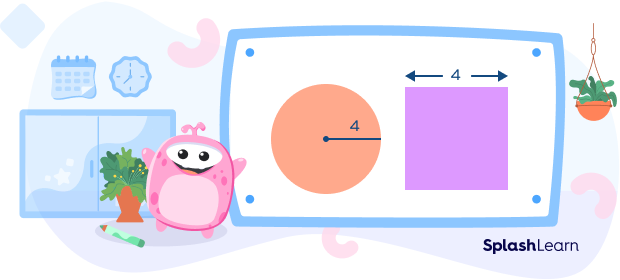
Now you will carry out the following calculations:

Perimeter of circle $= 2\pi r$

      $= 2 \times 3.14 \times 4$

      $= 25.13$ units

Perimeter of square $= 4 \times $ side

       $= 4 \times 4$

       $= 16$ units

Thus, we can conclude that 

Perimeter of the circle with radius 4 units $ \neq$ Perimeter of the Square with side 4 units 

Not Equal Sign in Real Life

We use the term “not equal to” on a regular basis in our day-to-day life. Here are some instances from real life:

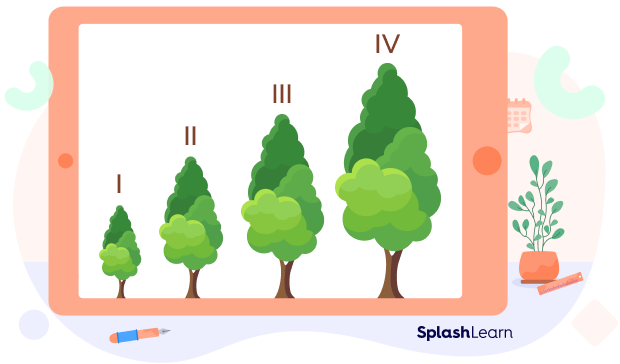
• When you compare the heights of people or objects, you can use the not equal to symbol to represent unequal heights. For instance, the heights of the four trees are not equal. 

• You go grocery shopping, and the storekeeper weighs the fruits for you. If there’s an imbalance, it means that the weight of fruits on the weighing balance is not equal to the weight placed on the other side. 

There are innumerable such instances that we can recall. What strikes your mind first when you think of using “not equal to” in real life? Think and write it down!

Facts about Not Equal to

Conclusion

In this article, we learned about the “not equal to” sign, its symbol, its uses, etc. Let’s solve a few examples and practice problems based on these concepts.

Solved Examples of the “Not Equal to” Sign

1. Solve the following equation: $6b \;-\; 35 = 55$ and find whether $b = 12$ or not. 

Solution: 

We will begin by solving the linear equation: 

$6b \;-\; 35 = 55$

$6b = 55 + 35$

$6b = 90$

$b = 906$

$b = 15$

Therefore, we can say that $b \neq 12$.

2. Bella spent $\$18$ out of her $\$20$ pocket money. John spent $\$13$ out of $\$15$. Calculate whether the percentage of money spent by each one of them is equal or not.

Solution: 

Percentage of money spent by Bella $= \frac{18}{20} \times 100$

$= \frac{9}{10} \times 100$ 

$= 90\%$

Percentage of money spent by John $= \frac{13}{15} \times 100$

$= \frac{13}{3} \times 25$

$= 86.66\%$

Thus, the percentage of money spent by Bella$\neq$ Percentage of money spent by John, as $90\% \neq 86.66\%$. 

3. Packet A contains 8 chocolates, and each chocolate weighs 4 ounces. Packet B has 12 chocolates, and each chocolate weighs 2 ounces. Find whether the two packets are equal in terms of weight.

Solution: 

Begin by calculating the total weight of both packets:

Total weight of chocolates in Packet A $=$ Number of chocolates weight of one chocolate 

$=8 \times 4$ ounce

$= 32$ ounces

Total weight of chocolates in packet B $=$ Number of chocolates weight of one chocolate 

  $=12 \times 2$ ounce

  $= 24$ ounces

We can say that the two packets are not equal in terms of weight.

4. The side of a square is 5 units. Determine whether the perimeter and area is equal or not.

Solution: 

The perimeter of square $= 4 \times $ side

$P = 4 \times 5$

$P = 20$ units

Area of square $= side \times side$

$A = 5 \times 5$

$A = 25$ square units

The perimeter of square is not equal to area of square, as $20 \neq 25$.

Practice Problems on “Not Equal to” Sign

Frequently Asked Questions on “Not Equal to” Sign