What Is an Obtuse Scalene Triangle?
An obtuse scalene triangle is a triangle characterized by one obtuse angle (angle between 90 degrees and 180 degrees) and three sides of different lengths. These triangles are both scalene and obtuse.
Triangles can be classified on the basis of side-lengths and angle measurements.
- On the basis of side-lengths: Equilateral Triangle (3 equal sides), Isosceles Triangle (2 equal sides) and Scalene Triangle (no equal side).
- On the basis of angle-measurements: Acute Triangle (all acute angles), Obtuse Triangle (one obtuse angle), Right Triangle (one right angle).
An Obtuse Scalene Triangle is a type of a triangle based on both sides and angles. It has all the properties of an obtuse triangle and a scalene triangle.
- Obtuse triangle: It is a triangle that has one obtuse angle, and two acute angles. So, how does an obtuse angle look like? Take a look!
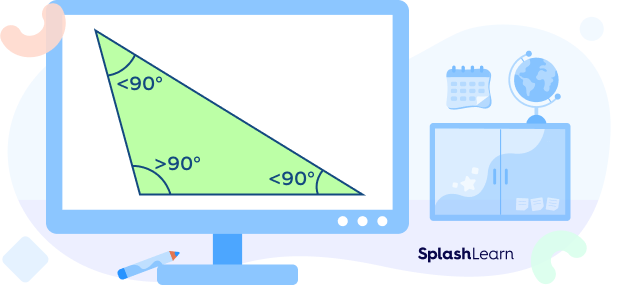
- Scalene triangle: It is a triangle where all three sides are of different lengths.

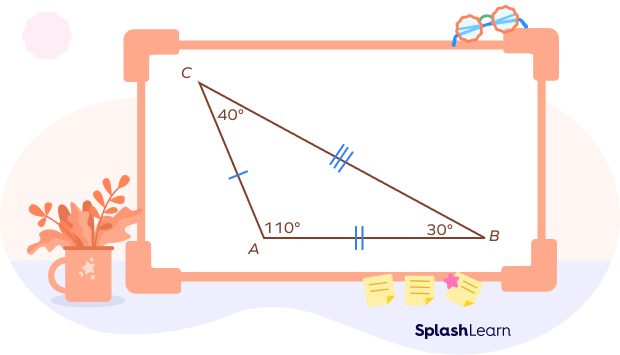
Obtuse Scalene Triangle Example:
In the given triangle, the angle A is an obtuse angle. The remaining two angles are acute. All three sides have different lengths. It is an obtuse scalene triangle.
Recommended Games
Obtuse Scalene Triangle: Definition
An obtuse scalene triangle is a triangle that has three sides of different measurements and one interior angle that is obtuse (between 90° and 180°).
Recommended Worksheets
Properties of an Obtuse Scalene Triangle
As mentioned earlier, an obtuse scalene triangle has the properties of both scalene and obtuse triangle.
- There are two acute angles (less than 90°) and one obtuse angle (between 90° and 180°).
- All the sides of an obtuse scalene triangle are of different lengths.
- All angles of an obtuse scalene triangle are different in measure.
- The side opposite to the obtuse angle is the longest side.
- The sum of all three interior angles of the obtuse scalene triangle is 180°.
Obtuse Scalene Triangle Formulas
Let’s discuss the formulas to find the area and perimeter of a scalene obtuse triangle.
Perimeter of an obtuse scalene triangle
The perimeter of an obtuse scalene triangle is the sum of the three sides. It is the total length of its outer boundary. Perimeter is measured in linear units such as inches, feet, etc.
P = (a + b + c)
where
a, b, and c are the lengths of the sides of the triangle.
Area of an obtuse scalene triangle area
Area of an obtuse scalene triangle is the total region covered within its boundary. Let’s understand how to find the area of an obtuse scalene triangle.
- Area using base and height:
Area $= \frac{1}{2} \times b \times h$
where
b is the base
h is the height of the triangle.
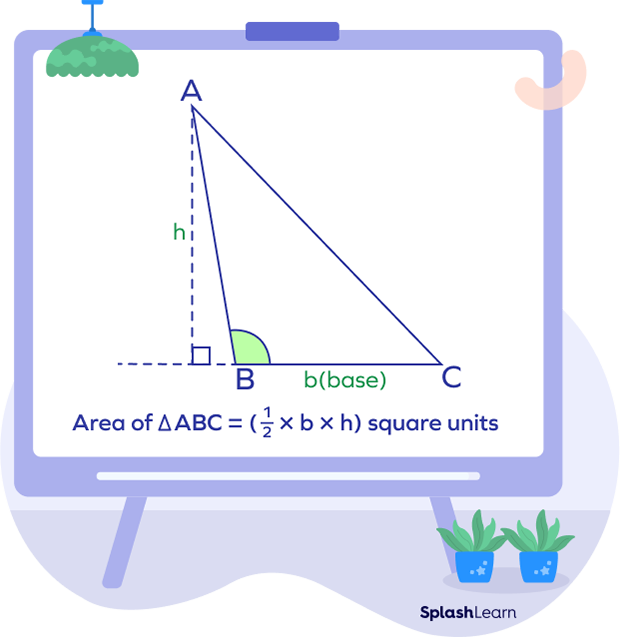
Note: The height of an obtuse angled triangle drawn will lie outside the triangle.
- Area using side-lengths
If all the sides of the scalene obtuse triangle are given, then the area of an obtuse scalene triangle can be calculated using Heron’s formula.
Area $= \sqrt{s(s – a)(s – b)(s – c)}$
where
s denotes the semi perimeter and $s = \frac{(a + b + c)}{2}$
a, b, and c are the sides of the given triangle.
Facts about Obtuse Scalene Triangle
- A scalene triangle can be an obtuse-angled triangle, acute-angled triangle, or a right-angled triangle.
- An obtuse triangle is a triangle that has one obtuse angle and two acute angles. It becomes an obtuse scalene triangle when the two acute angles are unequal.
- A scalene triangle becomes an obtuse scalene triangle if one of its interior angles is an obtuse angle.
Conclusion
In this article, we learned about the special triangle — Obtuse Scalene Triangle, along with its properties and associated formulas. Let’s move to the numerical section and solve a few examples and practice MCQs for better comprehension!
Solved Examples on Obtuse Scalene Triangle
1. Find the perimeter of an obtuse scalene triangle whose sides are 2 inches, 6.5 inches, and 8 inches.
Solution:
Side-lengths are 2 inches, 6.5 inches, and 8 inches.
Perimeter = Sum of all sides
Perimeter = 2 in + 6.5 in + 8 in
Perimeter = 16.5 inches
2. Find the area of an obtuse scalene triangle with height 12 units and base 14 units.
Solution:
Base (b) = 14 units
Height (h) = 12 units
Area $= \frac{1}{2} \times b \times h$
Area $= \frac{1}{2} \times 14 \times 12$
Area = 84 square units
3. If the area of an obtuse scalene triangle is 24 square inches and the base is 6 inches, what will be its height?
Solution:
Area of an obtuse scalene triangle (A) = 24 square inches
Base (b) = 6 inches
Area $= \frac{1}{2} \times b \times h$
Height $= \frac{2 \times Area}{Base}$
Height $= \frac{2 \times 24}{6}$Since we know the length of all sides, we will use the Heron’s formula.
Height =8 inches
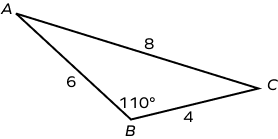
4. Find the area of the following obtuse scalene triangle.
Solution:
AB = a = 6 units
BC = b = 4 units
AC = c = 9 units
Since we know the length of all sides, we will use the Heron’s formula.
Semiperimeter $= s = \frac{a + b + c}{2} = \frac{6 + 4 + 8}{2} = \frac{18}{2} = 9$ units
Area $= \sqrt{s(s\;-\;a)(s\;-\;b)(s\;-\;c)}$
Area $= \sqrt{9(9\;-\;6)(9\;-\;4)(9\;-\;8)}$
Area $= \sqrt{8 \times 3 \times 5 \times 1}$
Area$ = \sqrt{120}$
Area $= 2\sqrt{30}$ square units
5. Find the third angle of the obtuse scalene triangle whose two angles are 20° and 30°.
Solution:
In △ABC, let m∠A = 20° and m∠B = 30°.
By the angle sum property, we write
m∠A + m∠B + m∠C = 180°
20° + 30° + m∠C = 180°
50° + m∠C = 180°
m∠C = 180° – 50° = 130°
Practice Problems on Obtuse Scalene Triangle
Obtuse Scalene Triangle: Definition with Examples
A scalene triangle is a triangle that has
A scalene triangle has three unequal sides.
A triangle having angles 130°, 30°, and 20° is
In an obtuse scalene triangle, there is one obtuse angle and two acute angles. Note that since three angles are of different measure, the sides must be of different lengths. So, it is an obtuse scalene triangle.
The three angles of a triangle are 34°, 36° and 110°. Which type of triangle is this?
There is an obtuse angle and two unequal acute angles. So, the angles 34°, 36°, and 110° form an obtuse scalene triangle.
Find the perimeter of the triangle given below?

Perimeter = Sum of all the sides
Perimeter = AB + BC + AC
Perimeter = 1.7 + 2.8 + 1.5
Perimeter = 6 units
Frequently Asked Questions about Obtuse Scalene Triangle
How can we draw an obtuse scalene triangle?
To draw an obtuse scalene triangle, the first step is to draw a line segment, which will be the base of the triangle.
Then we construct an obtuse angle on one end of that segment and join it with the other end of the segment. We will get an obtuse triangle.
What is the difference between an obtuse scalene triangle and an obtuse isosceles triangle?
An obtuse scalene triangle is a triangle, which has all sides unequal and one angle is more than 90°. An obtuse isosceles triangle is a triangle in which two sides are equal and one angle is more than 90°.
What is the difference between an obtuse scalene triangle and an acute scalene triangle?
An obtuse scalene triangle is a triangle which has all sides unequal and one angle is more than 90°. An acute scalene triangle is a triangle in which all sides are unequal and all angles are less than 90°.
Can an equilateral triangle be an obtuse scalene triangle?
No. An equilateral triangle has all sides equal, but an obtuse scalene triangle has all sides unequal.
What is a scalene right angled triangle?
A scalene right angled triangle is a triangle in which all sides are of different measure and one angle is 90°.




























