What Is a Parallelepiped in Math?
A parallelepiped is a three-dimensional geometric solid with six faces such that each face is a parallelogram. It is also called a prism with a parallelogram base.
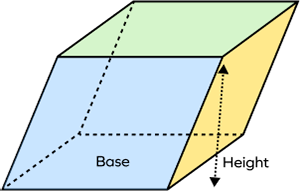
A parallelepiped is a polyhedron since it is formed by 6 parallelogram faces. A parallelogram is a quadrilateral whose opposite sides are equal and parallel to each other.
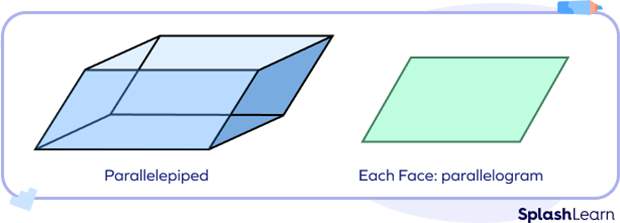
Definition of Parallelepiped
A parallelepiped is a three-dimensional shape with parallelogram-like faces. It is a polyhedron since it is made of polygons. It has sharp corners, straight edges, and polygon faces. It has three pairs of parallel faces joined together.
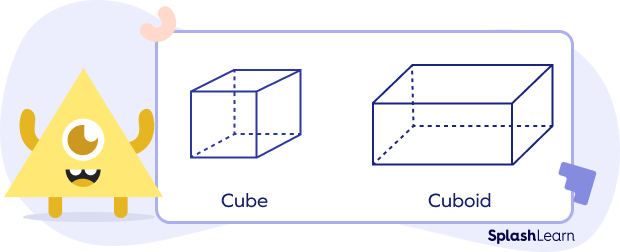
Its special cases are the cube and cuboid. All of the faces of the rectangular parallelepiped are rectangular.
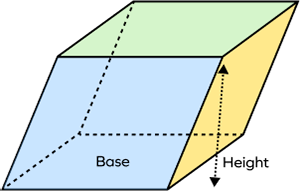
Properties of Parallelepiped
- It is a solid figure. It means that it has three dimensions.
- A parallelepiped has 6 faces, 12 edges, and 8 vertices.
- There are three pairs of parallel faces.
- The diagonal of each face refers to the “face diagonal.”
- From the outside, each face appears to be the mirror image of the opposite face.
- It is also referred to as a parallelogram-based prism.
- It has six faces. It is a polyhedron made of parallelograms.
- It is a hexahedron (a polyhedron with six faces).
Difference between Parallelogram and Parallelepiped
| Parallelogram | Parallelepiped |
|---|---|
 |  |
| It is a convex quadrilateral in which each pair of opposite edges are parallel and of equal length. It is a 2D figure. | A parallelepiped is a three-dimensional shape with 6 faces, each of which is a parallelogram. |
| Example: Square, Rectangle, Rhombus | Example: Cube, Cuboid, Rhomboid |
Surface Area of Parallelepiped
The total area covered by all parallelepiped surfaces is referred to as the parallelepiped’s total surface area. It means that the total area of the 6 parallelograms forming the faces of a parallelepiped defines the total surface area of the parallelepiped.
A parallelepiped’s surface area is measured in square units like $in^{2},\; ft^{2},\; yard^{2}$, etc. There are two types of parallelepiped surface area:
- Lateral surface area
- Total surface area
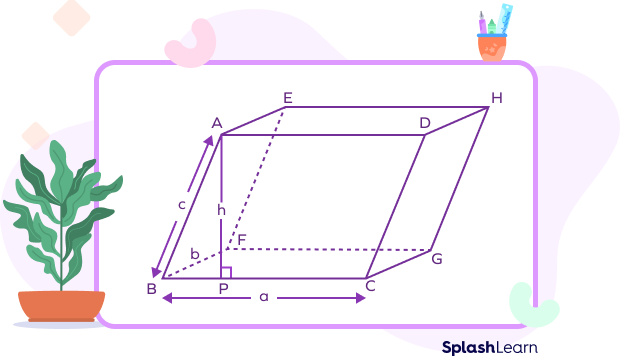
Lateral Surface Area of Parallelepiped
The area covered by the parallelepiped’s lateral or side faces is known as its lateral surface area. We determine the sum of the areas of four lateral faces in order to calculate the LSA of a parallelepiped.
In other words, we can say that the surface area of a parallelepiped’s face, excluding its base and top, is referred to as its lateral surface area.
Lateral Surface Area Formula (Bold)
- Lateral surface area (LSA) of parallelepiped $=$ Perimeter of base $\times$ Height
- Lateral surface area (LSA) $= 2(a + b) \times h$
where
a is the length of the base,
b is the breadth of the base,
and
h is the height of parallelepiped.
Total Surface Area of Parallelepiped
The total area that is covered by all the faces of a parallelepiped is known as the total surface area of the parallelepiped. We find the sum of the areas of all the six faces in order to calculate the TSA of a parallelepiped.
Total Surface Area of Parallelepiped Formula (Bold)
The formula for determining the lateral and total surface areas of the parallelepiped is as follows:
- Total surface area (TSA) $=$ LSA $+ 2$(Base area)
- Total surface area (TSA) $= [2(a + b) \times h] + 2$(Base area)
where a is the length, b is the breadth and h is the height of parallelepiped.
Volume of Parallelepiped
The total space that a parallelepiped occupies in a three-dimensional plane is called its volume. It is measured in cubic units like $in^{3},\; ft^{3},\; yard^{3}$, and so on.
Parallelepiped Volume Formula (Bold)
Let’s understand how to find the volume of a parallelepiped. The volume of the parallelepiped is given by the product the base area and height.
Volume of parallelepiped (V) $=$ Base Area $\times$ Height
Parallelepiped Formulas
| Lateral Surface Area (LSA) | Perimeter of base $\times$ Height |
| Total Surface Area (TSA) | LSA $+ 2$(Base area) |
| Volume (V) | Base Area $\times$ Height |
Rectangular Parallelepiped
A unique parallelepiped, with all six faces being rectangular in shape, is the rectangular parallelepiped, which is also known as a cuboid. All of the parallel edges have the same length. A typical rectangular parallelepiped is a shoebox.
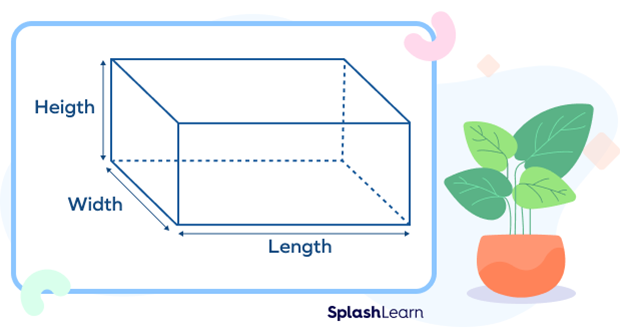
- Total surface area (TSA) $= 2(lb + bh + lh)$
- Volume (V) $= l \times b \times h$
- Diagonal (D) $= \sqrt{l^{2} + b^{2} + h^{2}}$
Where l, b, and h are the three dimensions.
Facts about Parallelepipeds
- Specific types of parallelepipeds include the rectangular cuboid with six rectangular faces, the cube with six square faces, and the rhombohedron with six rhombus faces.
- A prism whose base is a parallelogram is referred to as the parallelepiped.
- The length of the parallel edges of a parallelepiped is the same.
- The rectangular parallelepiped has three distinct faces that can be seen at the same time.
Conclusion
In this article, we learned about parallelepiped and rectangular parallelepiped shapes, their properties, formulas for surface area and volume. Let’s solve a few examples and practice problems on parallelepiped.
Solved Examples on Parallelepipeds
- Find the parallelepiped’s lateral surface area if its base face has opposite sides measuring 5 inches by 7 inches and a height of 6 inches.
Solution:
a $= 5$ inches and b $= 7$ inches
height $= 6$ inches
Applying the lateral surface area of the parallelepiped formula,
$\Rightarrow LSA = 2(a + b) \times h$
$\Rightarrow LSA = 2(5 + 7) \times 6 = 144\; inches^{2}$
- The sides of a parallelepiped’s base are given by 7 feet and 11 feet, respectively. The parallelepiped has a height of 8 feet. Find out how much it would cost to paint its lateral walls for $\$20$ per square foot.
Solution:
$a = 7$ feet, $b = 11$ feet
To find the cost to paint its side walls, first, we have to find the lateral surface area.
Applying the lateral surface area of the parallelepiped formula,
$ LSA = 2(a + b) \times h$
$\Rightarrow LSA = 2(7 + 11) \times 8 = 288$ sq. feet.
Now,
The cost of painting exterior walls $=$ Lateral surface area $\times$ cost per square foot.
$\therefore$ The cost of painting exterior walls $= 288 \times \$20 = \$5,760$
- A rectangular box has dimensions 5 in $\times$ 4 in $\times$ 3 in. Find the total surface area.
Solution:
The dimensions of a rectangular box are 5 in $\times$ 4 in $\times$ 3 in.
length (a) $= 5$ in, width (b) $= 4$ in, and height (h) $= 3$ in
Total surface area (TSA) $= 2(a \times b + b \times c + c \times a)$
$\Rightarrow TSA = 2 (5 \times 4 + 4 \times 3 + 3 \times 5)$
$\Rightarrow TSA = 2 (20 + 12 + 15)$
$\Rightarrow TSA = 94\; in^{2}$.
- If the base area of a parallelepiped is $70\;in^{2}$ and the height is 8 inches, then find its volume.
Solution:
The base area of a parallelepiped $= 70\; in^{2}$, height $= 8$ inches.
The volume of parallelepiped (V) $=$ Base Area $\times$ Height
$V = 70 \times 8 = 560\; in^{3}$.
- A rectangular parallelepiped has dimensions of 10 in, 5 in, and 4 in. Find the length of its diagonal.
Solution:
a $= 10$ in, b $= 5$ in, and c $= 4$ in.
The diagonal of rectangular parallelepiped $= \sqrt{a^{2} + b^{2} + c^{2}}$
$= \sqrt{10^{2} + 5^{2} + 4^{2}}$
$= \sqrt{141}$
$= 11.87$ in
Practice Problems on Parallelepipeds
Frequently Asked Questions on Parallelepipeds
How many edges and vertices does a parallelepiped have?
A parallelepiped has 12 edges and 8 vertices.
What is a rectangular parallelepiped?
A unique parallelepiped with all six faces being rectangular is the rectangular parallelepiped, which is also known as a cuboid.
What are the rectangular parallelepiped formulas?
The formula for calculating surface areas and volume for rectangular parallelepiped are as follows:
- Total surface area (TSA) $= 2(a \times b + b \times c + c \times a)$
- Volume (V) $= a \times b \times c$,
- Diagonal (D) $= \sqrt{a^{2} + b^{2} + c^{2}}$
where a, b, and c are the three dimensions.
What is the shape of a parallelepiped?
A parallelepiped is a three-dimensional shape with 6 parallelogram-like faces. It is a polyhedron, which means that it has six faces. It is made up of three pairs of parallel faces joined together. Its special cases are the cube and cuboid etc.
What are the real-life examples of a parallelepiped shape?
Some real-life examples of parallelepiped shapes are shoeboxes, bricks, cubes, etc.
Is a rectangle a parallelepiped?
No, a rectangle is a 2D shape, whereas a parallelepiped is a 3D shape (a polyhedron) where each face is a parallelogram.
Is a cube a parallelepiped?
A cube is a parallelepiped where each face is a square.
















